人教版九年级上册21.2.4 一元二次方程的根与系数的关系精品教案
展开第二十一章 一元二次方程
21.2 解一元二次方程
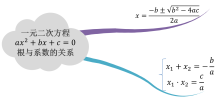
*21.2.4 一元二次方程的根与系数的关系
一、 教学目标
- 熟练掌握一元二次方程的根与系数的关系;
- 灵活运用一元二次方程的根与系数的关系解决实际问题;
- 经历探索一元二次方程的根与系数的关系,发展学生的逻辑推理和数学运算的核心素养,培养学生观察、分析、归纳和判断的能力;
- 通过探索一元二次方程的根与系数的关系,体验韦达定理的发现、不完全归纳证明以及演绎证明等整个数学思维过程,提升数学的学习兴趣;
- 提高学生综合运用知识分析解决较复杂问题的能力.
二、教学重难点
重点:一元二次方程的根与系数的关系.
难点:对一元二次方程的根与系数关系的理解和推导.
三、教学用具
多媒体课件
四、教学过程设计
教学环节 | 教师活动 | 学生活动 | 设计意图 |
教学目标 | 【学习目标】 1.熟练掌握一元二次方程的根与系数的关系; 2.灵活运用一元二次方程的根与系数的关系解决实际问题; 3.经历探索一元二次方程的根与系数的关系,发展学生的逻辑推理和数学运算的核心素养,培养学生观察、分析、归纳和判断的能力; 4.通过探索一元二次方程的根与系数的关系,体验韦达定理的发现、不完全归纳证明以及演绎证明等整个数学思维过程,提升数学的学习兴趣; 5.提高学生综合运用知识分析解决较复杂问题的能力. | 熟悉教学目标. | 通过学习目标让学生熟悉本节课要讲解的内容. |
环节一 创设情境 | 【引入】 法国数学家弗朗索瓦·韦达于1615年在《论方程的识别与订正》一书中建立了方程根与系数的关系.今天我们就跟随数学家韦达的脚步一起来探究一下:一元二次方程的根与系数的关系.(课件展示)
大家知道方程 | 聆听,或提前准备相关内容并于课上做补充展示.
学生倾听、思考,初步了解本节课所要探究的问题.
生答:应该有.
| 通过回顾数学文化的引入,让学生了解要探究的内容,助于对新知的引入和学习. |
环节二 探究新知 | 【思考与探究】 先来看看特殊情况,从因式分解法可知,方程
把方程
接下来我们考虑一般的情况.一般的一元二次方程
提问:如果把方程
师表扬并总结,通过上面的运算表明任何一个一元二次方程的根与系数的关系为:两个根的和等于一次项系数与二次项系数的比的相反数,两个根的积等于常数项与二次项系数的比. | 学生观察、思考,然后小组交流后回答. 预设生1:把
生2:二次项系数为1的方程,两根之和为一次项系数的负数,两根之积为常数项.
生3:我们可以用求根公式
生4:式子先化为 生5:当方程二次项系数不为1时,两根之和为一次项系数的负数比上二次项系数,两根之积为常数项比上二次项系数. | 通过思考问题,让学生知道二次项系数为1的一元二次方程的根与系数的关系,为后面的探究进行铺垫. 让学生通过探究问题体会由特殊到一般的认知过程. 经历探索一元二次方程的根与系数的关系,发展学生的逻辑推理和数学运算的核心素养. |
环节三 应用新知 | 【典型例题】 例:不解方程,求下列方程两个根的和与积:
(1) (3)
解:(1) (2) (3)方程化为一般式
教师可以找2名优异学生板演,对于易错点(方程要化成一般式)和难点加以强调和纠正,有助于学生运算正确,并且适当鼓励学生养成良好的运算习惯和建立学好数学的自信心. 【资料补充】 韦达(1540—1603),法国数学家.年轻时当过律师,后来致力于数学研究,韦达从事数学研究只是出于爱好,然而他却完成了代数和三角学方面的巨著,他是第一个有意识地和系统地使用字母来表示已知数、未知数及其乘幂的人,带来了代数理论研究的重大进步.他讨论了方程根的多种有理变换,发现了方程根与系数的关系(即韦达定理),他的《应用于三角形的数学定律》可能是西欧第一部论述用6种三角函数解平面和球面三角形方法的系统著作.在欧洲被尊称为“代数学之父”.(取自UMP平台资料)
师介绍,生聆听,也可以生介绍,师补充. | 学生按步骤独立作答后,组内讨论交流. 生1:对于(1)方程,二次项系数为1,则
生2:对于(2)方程,二次项系数为3,则
生3:对于(3)方程,二次项系数为4,则
生聆听并补充等. | 通过例题教学,加深对根与系数关系的理解,培养学生的应用意识及能力,同时感受到数学的美,从而建立学好数学的自信心.
|
环节四 巩固新知 | 巩固练习: 1.不解方程,求下列方程两个根的和与积; (1) (2) (3) (4)
解:(1)方程化为 (2)方程化为 (3)方程化为 (4)方程化为
2.小明和小红一起做作业,在解一道一元二次方程时,小明写错了常数项,解得两根为8和2;小红写错了一次项系数,解得两根为-9和-1.若二次项系数是1,你知道原来的方程是多少吗?
解:∵ 原方程二次项系数为1,∵ ∵ ∴ 原方程为:
教师可以找学生板演,对于易错点和难点加以强调和纠正,有助于学生运算正确,并且适当鼓励学生养成良好的运算习惯和建立学好数学的自信心. | 学生自主练习,然后组内讨论交流. 生1:方程化为 生2:方程化为 生3:方程化为 生4:方程化为 生5:∵ 原方程二次项系数为1,∵ ∵ ∴ 原方程为: | 进一步巩固本节课的内容. 了解学习效果,让学生经历运用知识解决问题的过程,给学生获得成功体验的空间.
|
环节五 课堂小结 | 思维导图的形式呈现本节课的主要内容:
问题:本节课你学到了什么?
| 生回顾总结,归纳本节课所学. 生1;学到了一元二次方程的根与系数的关系. 生2:当一元二次方程的系数为1时,两根之和为一次项系数的负数,两根之积为常数项. 生3:…… | 通过提问让学生回顾、总结公式法解一元二次方程的知识,并帮助学生梳理本节课所学内容. |
环节六 布置作业 | 教科书 第16页练习题; 第17页习题21.2第7题. |
|
|
初中数学人教版九年级上册21.1 一元二次方程获奖教案设计: 这是一份初中数学人教版九年级上册21.1 一元二次方程获奖教案设计,共7页。教案主要包含了教学重难点,教学用具,教学过程设计等内容,欢迎下载使用。
人教版九年级上册21.2.4 一元二次方程的根与系数的关系精品教案设计: 这是一份人教版九年级上册21.2.4 一元二次方程的根与系数的关系精品教案设计,共7页。教案主要包含了教学重难点,教学用具,教学过程设计等内容,欢迎下载使用。
人教版九年级上册21.2.4 一元二次方程的根与系数的关系教学设计: 这是一份人教版九年级上册21.2.4 一元二次方程的根与系数的关系教学设计,共4页。教案主要包含了知识与技能,过程与方法,情感态度,教学重点,教学难点,教学说明,归纳结论等内容,欢迎下载使用。