数学九年级上册第二十一章 一元二次方程21.2 解一元二次方程21.2.3 因式分解法精品教案
展开第二十一章 一元二次方程
21.2 解一元二次方程
21.2.3 因式分解法
一、 教学目标
- 了解因式分解法的概念;
- 会利用因式分解法解简单数字系数的一元二次方程;
- 经历探索因式分解法解一元二次方程,发展学生的逻辑推理和数学运算的核心素养,同时学会灵活选择解方程的方法;
- 通过运用因式分解法解简单系数的一元二次方程,体验解决问题的方法多样性,提升学习数学的兴趣,并建立学好数学的自信心.
二、教学重难点
重点:应用因式分解法解一元二次方程.
难点:将方程化为一般形式后,对方程左侧二次三项式进行因式分解.
三、教学用具
多媒体课件
四、教学过程设计
教学环节 | 教师活动 | 学生活动 | 设计意图 |
教学目标 | 【学习目标】 1.了解因式分解法的概念; 2.会利用因式分解法解简单数字系数的一元二次方程; 3.经历探索因式分解法解一元二次方程,发展学生的逻辑推理和数学运算的核心素养,同时学会灵活选择解方程的方法; 4.通过运用因式分解法解简单系数的一元二次方程,体验解决问题的方法多样性,提升学习数学的兴趣,并建立学好数学的自信心. | 熟悉教学目标. | 通过学习目标让学生熟悉本节课要讲解的内容. |
环节一 创设情境 | 【回顾】 问题1:什么叫因式分解?因式分解有哪些方法?
问题2:将下列各题因式分解: (1) (2) (3) | 预设生答:把一个多项式化成几个整式的积的形式,这样的式子变形叫做这个多项式的因式分解,也叫分解因式. 生2:因式分解的方法有提取公因式、公式法、十字相乘法等. | 通过回顾之前学习的知识,并借助学生解因式分解,唤醒记忆,为讲解因式分解法作铺垫,助于对新知的引入和学习. |
环节二 探究新知 | 【探究】 问题1:根据物理学规律,如果把一个物体从地面以10m/s的速度竖直上抛,那么物体经过x s离地面的高度(单位:m)为
分析:设物体经过x s落回地面,这时它离地面的高度为0,即____________.
思考:除配方法或公式法以外,能否找到更为简单的方法解这个方程?
思考:解方程时,二次方程是如何降为一次的? 师适当表扬,补充和总结:上述解法中,由①到②的过程,不是用开平方降次,而是先因式分解,使方程化为两个一次式的乘积等于0的形式,再使这两个一次式分别等于0,从而实现降次.这种解一元二次方程的方法叫做因式分解法. | 学生观察、思考,然后小组交流后回答.
预设生答: 生1 生2:因为是落回地面,所以方程右边应该为0,左边可以用因式分解,得到一个单项式乘上一个多项式,因式分解得到 生3:从上述描述,物体应该在2.04 s时落回地面,0 s时物体被上抛离开地面,此刻物体的高度是0m. 生4:因为因式分解,所以降次了. | 让学生先自己动手试着寻找 |
环节三 应用新知 | 【典型例题】 例:解下列方程 (1) 解:(1)因式分解,得 于是得
解:(2)移项、合并同类项得
因式分解,得
师:做题的过程和最后,总结一下因式分解法解一元二次方程的步骤.
教师可以找2名优异学生板演,对于易错点(如移项变号、方程右侧为0等)和难点加以强调和纠正,并让学生总结因式分解的解题思路,助于学生运算正确.
师点评总结:用因式分解法解一元二次方程的步骤:1.移项:将方程化为一般形式;2.分解:将方程的左边分解为两个一次式的乘积;3.转化:令每个一次式分别为0,得到两个一元一次方程;4.求解:解这两个一元一次方程,它们的解就是一元二次方程的解.
师适当鼓励学生养成良好的运算习惯和建立学好数学的自信心. | 学生按步骤独立作答后,组内讨论交流. 生1:对于(1)方程左边是0,我们对方程左边进行因式分解,使方程化为两个一次式的乘积等于0的形式,也就是 生2:对于(2)方程,先将左边化为0,方程为 生3:1.先将方程左边化为0;2.然后对方程左边进行因式分解,使方程化为两个一次式的乘积等于0的形式;3.再使这两个一次式分别等于0;4.求出两个结果. | 通过例1熟悉因式分解法解题步骤,并让学生感受多元方法解一元二次方程,同时感受到数学的美,从而建立学好数学的自信心.
|
环节四 巩固新知 | 巩固练习:
答案:
答案:
答案: 4.下列哪些方程用因式分解法求解比较方便? (1) (2) (4) 答案:都可以用. 需注意(3)式,18开方为 教师可以找学生板演,对于易错点和难点加以强调和纠正,有助于学生运算正确,并且适当鼓励学生养成良好的运算习惯和建立学好数学的自信心. | 学生自主练习,然后组内讨论交流. 预设生1: 预设生2: 预设生3:
预设生1:(1)、(2)和(4). 预设生2:(3)也是,可以将18开方为 | 进一步巩固本节课的内容. 了解学习效果,让学生经历运用知识解决问题的过程,给学生获得成功体验的空间.
|
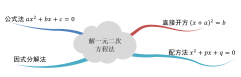
环节五 课堂小结 | 思维导图的形式呈现本节课的主要内容: 问题:本节课你学到了什么?能不能对解一元二次方程做一个总结?
四种基本解法比较
教师总结归纳: 配方法要先配方,再降次;通过配方法可以推出求根公式,公式法直接利用求根公式解方程;因式分解法要先将方程一边化为两个一次因式相乘,另一边为0,再分别使各一次因式等于0.配方法、公式法适用于所有一元二次方程,因式分解法在解某些一元二次方程时比较简便.总之,解一元二次方程的基本思路是:将二次方程化为一次方程,即降次. | 生1;因式分解法解一元二次方程. 生2:解一元二次方程有公式法、直接开方法、因式分解法、配方法. 生3:……
| 通过提问让学生回顾、总结公式法解一元二次方程的知识,并帮助学生梳理本节课所学内容. |
环节六 布置作业 | 教科书 第11页练习第1-2题; 第16页习题21.2第6题. |
|
|
初中数学人教版九年级上册21.2.3 因式分解法优秀教案设计: 这是一份初中数学人教版九年级上册21.2.3 因式分解法优秀教案设计,共6页。教案主要包含了教学重难点,教学用具,教学过程设计等内容,欢迎下载使用。
人教版九年级上册21.2.3 因式分解法教案设计: 这是一份人教版九年级上册21.2.3 因式分解法教案设计,共13页。教案主要包含了教学目标,课型,课时,教学重难点,课前准备,教学过程,课后作业,板书设计等内容,欢迎下载使用。
人教版九年级上册第二十一章 一元二次方程21.2 解一元二次方程21.2.3 因式分解法教案设计: 这是一份人教版九年级上册第二十一章 一元二次方程21.2 解一元二次方程21.2.3 因式分解法教案设计,共3页。教案主要包含了复习引入,探究新知,课堂训练,小结归纳,作业设 计等内容,欢迎下载使用。