




八年级上册13.3.1 等腰三角形说课课件ppt
展开1.理解并掌握等腰三角形的两条性质.(重点)2.经历探索等腰三角形的性质的过程,并能运用等腰三角形的性质解决问题.(难点)
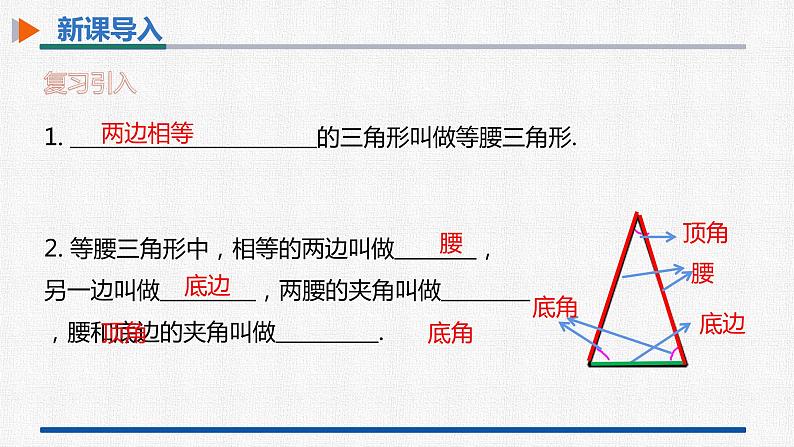
1. 的三角形叫做等腰三角形.
2. 等腰三角形中,相等的两边叫做 ,另一边叫做 ,两腰的夹角叫做 ,腰和底边的夹角叫做 .
3.等腰三角形具备一般三角形所有的性质,如内角和为 °;两边之和 第三边,两边之差 第三边.
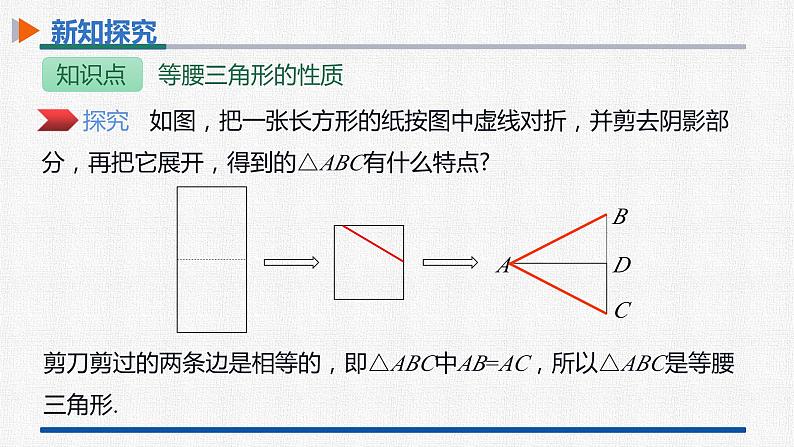
探究 如图,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点?
剪刀剪过的两条边是相等的,即△ABC中AB=AC,所以△ABC是等腰三角形.
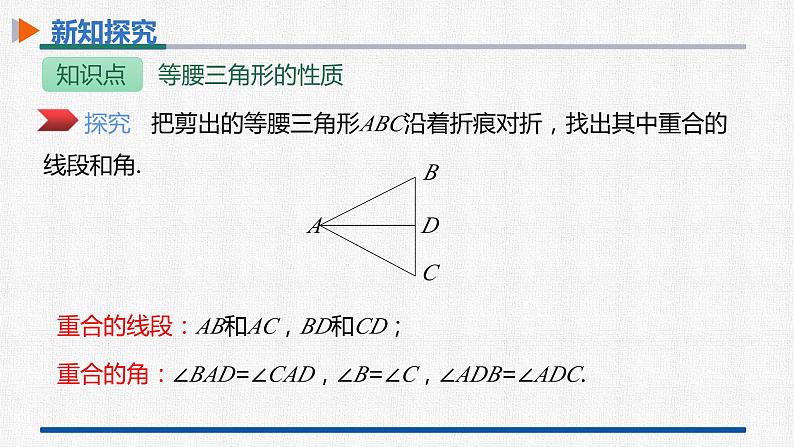
探究 把剪出的等腰三角形ABC沿着折痕对折,找出其中重合的线段和角.
重合的线段:AB和AC,BD和CD;
重合的角:∠BAD=∠CAD,∠B=∠C,∠ADB=∠ADC.
重合的线段:AB和AC,BD和CD;重合的角:∠B=∠C, ∠BAD=∠CAD, ∠ADB=∠ADC.
由这些的重合的线段和角,你能发现等腰三角形的性质吗?说一说你的猜想.
猜想AD为△ABC底边BC上的中线.
猜想AD为△ABC顶角的平分线.
猜想AD为△ABC底边BC上的高线.
猜想等腰三角形的两个底角相等.
2.猜想AD既是△ABC顶角的平分线,也是底边BC上的中线、高线.
在一张白纸上任意画一个等腰三角形,把它剪下来,请你试着折一折,你的猜想仍然成立吗?
如图,在△ABC中,AB=AC,
作底边的中线AD,则BD=CD.
∴ △BAD≌ △CAD (SSS).
∴∠B= ∠C,∠BAD= ∠CAD,∠ADB= ∠ADC.
又AB=AC,AD=AD,
∵∠ADB+∠ADC=180°,∴∠ADB= ∠ADC=90°,即AD⊥BC.
该性质定理的几何语言:
如图,在△ABC中,∵AB=AC,∴∠B=∠C.
如图,在△ABC中,①∵AB=AC,AD平分∠BAC,∴AD⊥BC,BD=CD.②∵AB=AC,AD⊥BC, ∴AD平分∠BAC,BD=CD.③∵AB=AC,BD=CD, ∴AD平分∠BAC,AD⊥BC.
例1 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
解:∵AB=AC,BD=BC=AD,∴∠ABC=∠C=∠BDC,∠A=∠ABD(等边对等角).设∠A=x,则∠BDC=∠A+∠ABD=2x,从而∠ABC=∠C=∠BDC=2x,于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180° .解得x=36°.所以,在△ABC中,∠A=36°,∠ABC=∠C=72°.
例2 (2020•青海)等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )A.55°, 55° B.70°, 40°或70°, 55°C.70°, 40° D. 55°,55°或70°, 40°
【解析】因为题干中没有说明70°角是顶角还是底角,所以应分情况讨论.当70°的角是底角时,顶角的度数为40°;当70°的角是顶角时,两底角相等,均为55°.故选D.
【变式】等腰三角形的一个内角为100°,则另外两个内角的度数分别是 .
【解析】题干中没有说明100°角是顶角还是底角,但分析可知,该角只能是顶角.而两底角相等,根据三角形的内角和定理易得底角是40°.
(1)“等边对等角”是证明三角形中两个角相等的常用方法,这种方法比利用三角形全等证明两个角相等更方便.(2)在等腰三角形中,依据三角形内角和等于180°,可以由顶角求底角,也可以由底角求顶角.
(2)如果已知一个内角,则这个角可能是底角也可能是顶角,要分两种情况讨论.
(3)等腰三角形的顶角可以是直角、钝角、锐角,而底角只能是锐角.
【变式】如图,在△ABC中,已知AB=AC,D为BC的中点,若∠BAD=35°,则∠C的度数为( )A.35° B.45° C.55° D.60°
例3 如图, AD是等腰三角形ABC的顶角平分线, BD=5,则CD等于( )A.10 B.5 C.4 D.3
例4 如图,已知AB=AC,点D,E在△ABC的边BC上,且AD=AE,求证:BD=CE.
证明:过点A作AG⊥BC于点G.
∵AB=AC,AD=AE,∴BG=CG,DG=EG,∴BG-DG=CG-EG,∴BD=CE.
(1)“三线合一”这一性质应用非常广泛,可以用来证明角相等、线段相等或线段垂直,也是等腰三角形中常作的辅助线.(2)等腰三角形是轴对称图形,对称轴为顶角平分线(或底边上的高或底边上的中线)所在的直线.
等腰三角形的两个底角相等(简写成“等边对等角”).
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(简写成“三线合一”).
该性质是指在同一个三角形中
在等腰三角形中,且为顶角的平分线、底边上的高和中线才有这一性质.
1.(2021•兰州模拟)如图,等腰三角形ABC中,AB=AC,∠A=46°,CD⊥AB于D,则∠DCB等于( )A.33° B.30° C.26° D.23°
2.(2021•赤峰)如图,AB∥CD,点E在线段BC上,CD=CE .若∠ABC=30°,则∠D的度数为( )A. 85° B.75° C.65° D.30°
3.(2021•陕西模拟)如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=2,则BF的长为( )A.3 B.4 C.5 D.6
4.下列说法正确的有 .(填序号)①等腰三角形的顶角一定是钝角.②等腰三角形的底角可能是锐角,也可能是直角或者钝角.③钝角三角形不可能是等腰三角形. ④等腰三角形的顶角平分线一定垂直底边.⑤等腰三角形的角平分线、中线和高互相重合.⑥等腰三角形底边上的中线一定平分顶角.
5.(1)等腰三角形一个底角为65°,则它的另外两个角为 ;(2)等腰三角形一个角为36°,则它的另外两个角为 ;(3)等腰三角形一个角为90°,则它的另外两个角为 .
72°,72°或36°,108°
6.(2021•武汉模拟)△ABC中,D、E在BC上,且EA=EB,DA=DC,若∠EAD=30°,则∠BAC= .
【解析】∵∠EAD=30°,∴∠AED+∠ADE=150°,∵EA=EB,DA=DC,∴∠B=∠BAE,∠C=∠CAD,又∠AED+∠ADE=∠B+∠BAE+∠C+∠CAD,∴∠AED+∠ADE=2∠BAE+2∠CAD,即150°=2(∠BAE+∠CAD),∴∠BAE+∠CAD=75°,∴∠BAC=75°+30°=105°.故答案为105°.
7.在△ABC中,AB=AC,∠B的角平分线与AC边所夹的锐角为60°,求∠A的度数.
8.如图,在△ABC中,AB=AC,∠BAC、∠ABC的角平分线相交于点D.若∠ADB=125°,求∠BAC得度数.
方法一:解:设∠BAC=4x.∵在△ABC中,AB=AC,∴∠ABC=(180°﹣4x)÷2=90°﹣2x.∵BD是∠ABC的角平分线,AD是∠BAC的角平分线,∴∠ABD=(90°﹣2x)÷2=45°﹣x,∠DAB=2x.∵∠ABD+∠DAB+∠ADB=180°,∴45°﹣x+2x+125°=180°.解得x=10°.∴∠BAC=40°.
人教版13.3.1 等腰三角形教学ppt课件: 这是一份人教版<a href="/sx/tb_c88618_t3/?tag_id=26" target="_blank">13.3.1 等腰三角形教学ppt课件</a>,共32页。PPT课件主要包含了等腰三角形,情境引入,导入新课,互动探究,讲授新课,ABAC,AB与AC,BD与CD,AD与AD,∠B与∠C等内容,欢迎下载使用。
初中数学人教版八年级上册13.3.1 等腰三角形优质ppt课件: 这是一份初中数学人教版八年级上册13.3.1 等腰三角形优质ppt课件,共18页。PPT课件主要包含了轴对称,底边上的中,底边上的高,等边对等角,三线合一等内容,欢迎下载使用。
数学八年级上册13.3.1 等腰三角形集体备课课件ppt: 这是一份数学八年级上册13.3.1 等腰三角形集体备课课件ppt,共26页。PPT课件主要包含了学习目标,新课导入,新课讲解,课堂小结,当堂小练,拓展与延伸,布置作业,等腰三角形,请完成对应习题等内容,欢迎下载使用。













