2023年华师大版数学八年级上册《12.3 乘法公式》课时练习（含答案）

2023年华师大版数学八年级上册

《12.3 乘法公式》课时练习

一              、选择题

1.下列运算正确的是(  )

A.5m+2m=7m2                  B.-2m2•m3=2m5       C.(-a2b)3=﹣a6b3                 D.(b+2a)(2a-b)=b2﹣4a2

2.下列多项式的乘法能用平方差公式计算的是(　　)

A.(﹣a﹣b)(a﹣b)    B.(﹣x+2)(x﹣2)

C.(﹣2x﹣1)(2x+1)   D.(﹣3x+2)(﹣2x+3)

3.下列式子正确的是(      )

A.(a﹣b)2=a2﹣2ab+b2                                    B.(a﹣b)2=a2﹣b2

C.(a﹣b 2=a2+2ab+b2                             D.(a﹣b)2=a2﹣ab+b2

4.我们已经接触了很多代数恒等式，知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式.例如图甲可以用来解释(a+b)2﹣(a﹣b)2=4ab.那么通过图乙面积的计算，验证了一个恒等式，此等式是(　　)

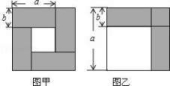
A.a2﹣b2=(a+b)(a﹣b)       B.(a﹣b)(a+2b)=a2+ab﹣b2

C.(a﹣b)2=a2﹣2ab+b2               D.(a+b)2=a2+2ab+b2

5.如图所示，从边长为a的大正方形中挖去一个边长是b的小正方形，小明将图a中的阴影部分拼成了一个如图b所示的长方形，这一过程可以验证(　　)

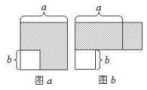
A.a2+b2﹣2ab=(a﹣b)2                              B.a2+b2+2ab=(a+b)2

C.2a2﹣3ab+b2=(2a﹣b)(a﹣b)                       D.a2﹣b2=(a+b)(a﹣b)

6.若4x2+axy+25y2是一个完全平方式，则a=(　　)

A.20          B.﹣20       C.±20          D.±10

7.计算(a－b)(a+b)(a2+b2)(a4－b4)的结果是(      )

A.a8+2a4b4+b8      B.a8－2a4b4+b8       C.a8+b8        D.a8－b8

8.如果(2a+2b+1)(2a+2b-1)=3，那么a＋b的值为(     )

A.2        B.±2         C.4      D.±1

二              、填空题

9.化简：(x+1)(x﹣1)+1=          .

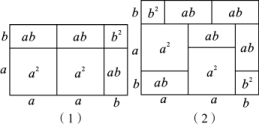
10.在我们所学的课本中，多项式与多项式相乘可以用几何图形的面积来表示.例如，(2a+b)(a+b)=2a2+3ab+b2就可以用图(1)来表示.请你根据此方法写出图(2)中图形的面积所表示的代数恒等式：            .

11.若(a＋b)2=17，(a－b)2=11，则a2＋b2=       .

12.若x2﹣mx+4是完全平方式，则m=　　    ．

13.若a＋b＝17，ab＝60，则a﹣b的值是__________．

14.观察下列等式：12﹣02＝1,22﹣12＝3,32﹣22＝5,42﹣32＝7,…,用含自然数n的等式表示这种规律　         　. 

三              、解答题

15.化简：x(4x+3y) -(2x+y)(2x-y).

16.化简：(2a﹣3b)(﹣3b﹣2a)

17.化简：(x＋5)(x﹣1)＋(x﹣2)2.

18.化简：(a＋b－c)(a＋b＋c)．

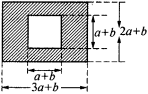
19.如图，某市有一块长为(3a+b)米，宽为(2a+b)米的长方形地块，规划部门计划将阴影部分进行绿化，中间将修建一座雕像，则绿化的面积是多少平方米？并求出当a=3,b=2时的绿化面积.

20.先化简，再求值：2(x-2)(x+9)+(x+3)(3-x)-(x-3)2，其中x=-3.

21.已知x+y=5，xy=1.

(1)求x2+y2的值.

(2)求(x﹣y)2的值.

22.对于任意有理数a、b、c、d，我们规定符号(a，b)⊙(c，d)=ad－bc.例如：(1，3)⊙(2，4)=1×4－2×3=－2.

(1)(－2，3)⊙(4，5)=________；

(2)求(3a＋1，a－2)⊙(a＋2，a－3)的值，其中a2－4a＋1=0.

参考答案

1.C

2.A

3.A

4.C

5.D

6.C

7.D

8.D

9.答案为：x2.

10.答案为：(a+2b)(2a+b)=2a2+5ab+2b2.

11.答案为：14.

12.答案为：±4．

13.答案为：±7.

14.答案为：n2﹣(n﹣1)2＝2n﹣1.

15.解：原式=3xy+y2.

16.解：原式(2a﹣3b)(﹣3b﹣2a)

=﹣6ab﹣4a2+9b2+6ab

=﹣4a2+9b2

17.原式＝2x2﹣1.

18.原式＝(a＋b)2﹣c2＝a2＋b2﹣c2＋2ab.

19.解：S阴影=(3a+b)(2a+b)﹣(a+b)2

=6a2+3ab+2ab+b2﹣a2﹣2ab﹣b2

=5a2+3ab(平方米)
当a=3，b=2时，

5a2+3ab=5×9+3×3×2=45+18=63(平方米).

20.解：原式=- 96.

21.解：(1)∵x+y=5，xy=1，

∴原式=(x+y)2﹣2xy=25﹣2=23；

(2)∵x+y=5，xy=1，

∴原式=(x+y)2﹣4xy=25﹣4=21.

22.解：(1)﹣22;

(2)(3a＋1，a﹣2)⊙(a＋2，a﹣3)＝(3a＋1)(a﹣3)﹣(a﹣2)(a＋2)

＝3a2﹣9a＋a﹣3﹣(a2﹣4)

＝3a2﹣9a＋a﹣3﹣a2＋4

＝2a2﹣8a＋1.

∵a2﹣4a＋1＝0，

∴2a2﹣8a＝﹣2，

∴(3a＋1，a﹣2)⊙(a＋2，a﹣3)＝﹣2＋1＝﹣1.