2023年华师大版数学八年级上册《12.2 整式的乘法》课时练习（含答案）

2023年华师大版数学八年级上册

《12.2 整式的乘法》课时练习

一              、选择题

1.下列计算正确的是(　　)

A.3x﹣2x=1                     B.3x+2x=5x2                     C.3x•2x=6x                   D.3x﹣2x=x

2.计算(－x)·(－2x2)(－4x4)的结果为(　　)

A.－4x6        B.－4x7        C.4x8        D.－4x8

3.计算：x（x2﹣1）=（　　）

A．x3﹣1        B．x3﹣x        C．x3+x        D．x2﹣x

4.计算(﹣2m)2•(﹣m•m2+3m3)的结果是(　 　)

A．8m5         B．﹣8m5           C．8m6        D．﹣4m4+12m5

5.若(x＋a)与(x＋3)的乘积中不含x的一次项，则a的值为(　　)

A.3        B.﹣3        C.1        D.﹣1

6.若(﹣2x+a)(x﹣1)中不含x的一次项，则(　　)

A.a=1             B.a=﹣1           C.a=﹣2          D.a=2

7.现规定一种运算：a*b=ab+a-b，其中a,b为实数，则a*b+(a-b)*b等于(　  　).

A.a2-b       B.b2-b       C.b2        D.b2-a

8.若M＝(a＋3)(a﹣4)，N＝(a＋2)(2a﹣5)，其中a为有理数，则M、N的大小关系是(　　)

A.M＞N        B.M＜N        C.M＝N         D.无法确定

二              、填空题

9.计算：﹣3x2•2x=______

10.计算：(﹣0.25)15×(﹣4)12=______．

11.已知单项式M、N满足等式3x(M-5x)=6x2y3+N，则M=______，N=______.

12.计算(1＋a)(1-2a)＋a(a-2)=________.

13.定义运算a#b=a(1-b)，下列给出了关于这种运算的几个结论：

①2#(-2)=6；

②a#b=b#a；

③若a+b=0，则(a#a)+(b#b)=2ab；
④若a#b=0，则a=0或b=1.

其中正确结论的序号是        .

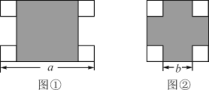
14.一个大正方形和四个相同的小正方形按图①，②两种方式摆放，则图②的大正方形中未被小正方形覆盖部分的面积是           .(用a，b的代数式表示)

三              、解答题

15.计算：(－3ab2)3·(－ac)2

16.计算：(－5x2y)(2x2－3x－2)

17.计算：(x+3)(x+4)﹣x(x﹣1)

18.计算：(a-2b-3c)(a-2b＋3c).

19.先化简，再求值：4x(2x2－x＋1)＋2(2x－1)－(1－2x2)，其中x=1；

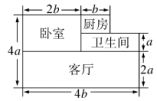
20.王老师家买了一套新房，其结构如图所示(单位：米)．他打算将卧室铺上木地板，其余部分铺上地砖．

(1)木地板和地砖分别需要多少平方米？

(2)如果地砖的价格为每平方米x元，木地板的价格为每平方米3x元，那么王老师需要花多少钱？

21.老师在黑板上布置了一道题：

已知x=-2，求式子(2x-y)(2x＋y)＋(2x-y)(y-4x)＋2y(y-3x)的值.

小亮和小新展开了下面的讨论：

小亮：只知道x的值，没有告诉y的值，这道题不能做；

小新：这道题与y的值无关，可以求解；

根据上述说法，你认为谁说的正确？为什么？

22.问题探究：

(1)运用多项式乘法，计算下列各题：

①(x+2)(x+3)=　   　

②(x+2)(x﹣3)=　   　

③(x﹣3)(x﹣1)=　   　

(2)若：(x+a)(x+b)=x2+px+q，根据你所发现的规律，直接填空：p=　   　，q=　   　.(用含a、b的代数式表示)

参考答案

1.D

2.B

3.B

4.A

5.B.

6.C

7.B

8.B

9.答案为：﹣6x3　

10.答案为：﹣．

11.答案为：2xy3；-15x2.

12.答案为：-a2-3a＋1

13.答案为：①③④；

14.答案为：ab.

15.原式=－3a5b6c2

16.原式=-10x4y+15x3y+10x2y.

17.原式=8x+12．

18.原式=[(a-2b)-3c][(a-2b)＋3c]=(a-2b)2-(3c)2=a2-4ab＋4b2-9c2.

19.原式=8x3-2x2+8x-3.

将x=1代入，原式=11.

20.解：(1)卧室的面积是2b(4a﹣2a)＝4ab(平方米)，

厨房、卫生间、客厅的面积和是b·(4a﹣2a﹣a)＋a·(4b﹣2b)＋2a·4b＝ab＋2ab＋8ab＝11ab(平方米)，

即木地板需要4ab平方米，地砖需要11ab平方米.

(2)11ab·x＋4ab·3x＝11abx＋12abx＝23abx(元)，即王老师需要花23abx元.

21.解：小新的说法正确.

∵(2x-y)(2x＋y)＋(2x-y)(y-4x)＋2y(y-3x)

=4x2-y2-8x2＋6xy-y2＋2y2-6xy=-4x2，

∴小新的说法正确.

22.解：(1)①(x+2)(x+3)=x2+3x+2x+6=x2+5x+6，

②(x+2)(x﹣3)=x2﹣3x+2x﹣6=x2﹣x﹣6，

③(x﹣3)(x﹣1)=x2﹣x﹣3x+3=x2﹣4x+3，

故答案为：x2+5x+6、x2﹣x﹣6、x2﹣4x+3；

(2)∵(x+a)(x+b)=x2+bx+ax+ab=x2+(a+b)x+ab，

∴x2+(a+b)x+ab=x2+px+q，

∴p=a+b、q=ab，

故答案为：a+b、ab.