数学八年级上册13.2.1 作轴对称图形公开课教案及反思

八年级上册13.2.1画轴对称图形  教案

【学习目标】

1．能作轴对称图形，能应用轴对称进行简单的图案设计；

2．能用轴对称的知识解决相应的数学问题．初步掌握一个点关于x轴或y轴对称的点的坐标变化规律；

3．通过独立思考、交流讨论、展示质疑，发展观察、归纳、想象及推理能力．

【学习重难点】

重点：作轴对称图形．

难点：用轴对称知识解决相应的数学问题．

【教学内容】

一、新知探究

探究点一

问题：作出点A关于 l 的对称点A′

作法：

1．过点A作l的____线，垂足为B；

2．在_____线上截取_____＝_______；

3．点______就是点A关于直线l的对称点．

探究点二

作出线段AB关于直线 l成轴对称的图形

问题1：第一种情况（图形在对称轴同一侧）

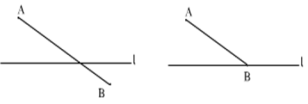
如图，已知线段AB和直线l，画出线段AB关于直线l对称的图形．

作法：

1. 过点A作l的____线，垂足为_____；在_____线上

截取____＝____；点___就是点A关于直线l的对称点．

2．同理，分别作出点B关于直线l的对称点__________．

3．连接__________．

4．则线段A′B′即为所求．

问题2：第二种情况（图形与对称轴相交）

探究点三

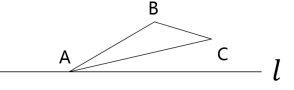
问题1：如图，已知△ABC和直线l，画出△ABC关于直线l对称的图形．

问题2：如图，已知△ABC和直线l，画出△ABC关于直线l对称的图形

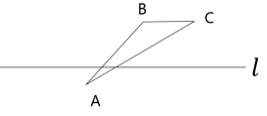
问题3：如图，已知△ABC和直线，画出△ABC关于直线对称的图形．

思考：通过以上探究，你能总结出作轴对称图形的方法吗?

归纳结论：

几何图形都可以看作由点组成．对于某些图形，只要作出图形中一些特殊点（如线段端点）的________，连接这些对称点，就可以得到原图形的____________．

二、随堂检测

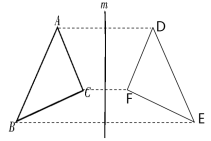
1．已知：△ABC，直线m．求作：△DEF，使△DEF与△ABC关于直线m对称．

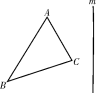
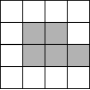
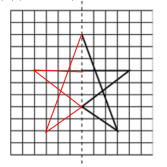
2．如图，在方格纸中给出了一个图案的一半，其中的虚线是这个图案的对称轴．在方格纸中画出该图案的另一半．

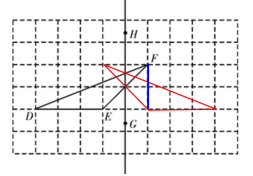
3．如图，在正方形网格中有一个△DEF和直线HG．

(1)作△DEF关于直线HG的轴对称图形；

(2)作△DEF的边DE上的高；

(3)若网格上的最小正方形边长为1，求△DEF的面积．

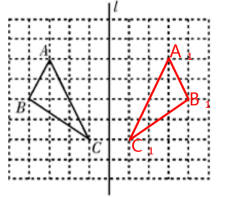
4．如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点分别在格点上，请在网格中按要求作出下列图形，并标注相应的字母．

①作△A1B1C1，使得△A1B1C1与△ABC关于直线l对称；

②△A1B1C1的面积为________．

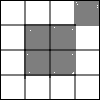
5．在4×4的方格中有五个同样大小的正方形如图摆放，移动其中一个正方形到空白方格中，与其余四个正方形组成的新图形是一个轴对称图形，这样的移法共有多少种？画出其中一个图形．

课堂小结

1．画出点A关于 l 的对称点A'（作法）．

2．作出与线段AB关于直线 l成轴对称的图形．

3．作一图形关于某直线对称的图形的关键是什么？

参考答案

探究点一

1．垂

2．线段AB延长     BA′

3．A′

探究点二

1．垂     线段AC延长     CA′   CA    A′

2．B′

3．A′B′

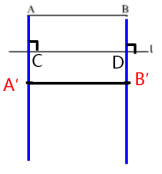
问题2：第二种情况

探究点三

问题1：

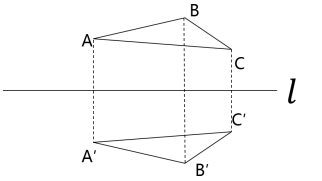
问题2：

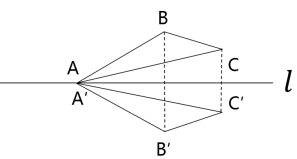
问题3：

归纳结论：

对称点       对称图形

随堂检测

1．

2．

3．(1) (2)如图

(3)△DEF的面积＝3

4．①如图

②4　

5．