






初中数学人教版(2024)八年级上册13.2.1 作轴对称图形一等奖ppt课件
展开你们会利用轴对称进行简单的图案设计吗?今天我们就一起来学习怎样作轴对称图形.
(1)知道轴对称变换前后的两个图形是全等的,并且任意一对对应点所连线段被对称轴垂直平分.
(2)已知一个图形和一条直线,会作出与这个图形关于这条直线对称的图形.
探究并归纳轴对称图形的性质
(1)这些图案有什么共同特点? (2)能否根据其中的一部分画出整个图案?
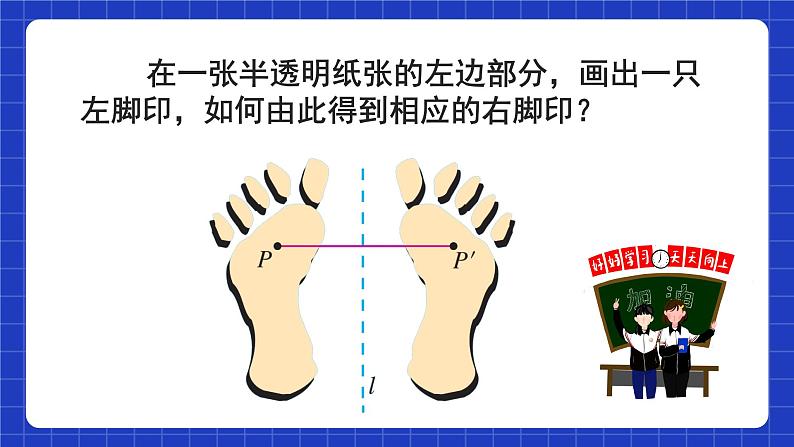
在一张半透明纸张的左边部分,画出一只左脚印,如何由此得到相应的右脚印?
请动手在一张纸上画一个你喜欢的图形,将这张纸折叠,描图,再打开纸,看看你得到了什么?
由一个平面图形可以得到与它关于一条直线l 对称的图形,这个图形与原图形的形状、大小完全相同;
新图形上的每一点都是原图形上的某一点关于直线 l 的对称点;
连接任意一对对应点的线段被对称轴垂直平分.
(1)由一个平面图形可以得到它关于一条直线l对称的图形,这个图形与原图形的_____、_____完全相同;
(2)新图形上的每一点,都是原图形上的某一点关于直线l的________;
(3)连接任意一对对应点的线段都被对称轴_________.
(4)两个图形关于某条直线对称,如果它们的对应线段或延长线相交,那么交点一定在________上.
如果有一个图形和一条直线,如何画出这个图形关于这条直线对称的图形呢?
例1 如图,已知△ABC 和直线l,画出与△ABC关于直线l 对称的图形.
作一个图形关于一条直线的对称图形
画法:(1)如图,过点A 画直线l 的垂线,垂足为点O,在垂线上截取OA′=OA,点A′就是点A 关于直线l 的对称点;(2)同理,分别画点B,C 关于直线l 的对称点B′,C′;
(3)连接A′B′,B′C′,C′A′,则△A′B′C′即为所求.
如何验证画出的图形与△ABC 关于直线l 对称?
画好后,可以通过折叠的方法验证一下.
几何图形都可以看作由点组成. 对于某些图形,只要画出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
已知一个几何图形和一条直线,说一说画一个与该图形关于这条直线对称的图形的一般方法.
练习2 如图,把下列图形补成关于直线 l 对称的图形.
【课本P68 练习 第1题】
练习3 用纸片剪一个三角形,分别沿它一边的中线、高、角平分线对折,看看哪些部分能够重合,哪些部分不能重合.
【课本P68 练习 第2题】
1.已知:直线AB与直线A′B′交于点P,并且这两条直线关于直线l成轴对称,下列说法正确的是( )
A.直线AB与直线A′B′的长度不相等B.直线AB、A′B′与直线l不一定能交于 同一点C.直线AB、A′B′与直线l一定交于P点D.点P关于直线l的对称点不存在
2.如图,把下列图形补成关于直线l对称的图形.
3.如图所示,∠AOB内一点P,P1、P2分别是P关于OA、OB的对称点,P1P2交OA于M,交OB于N.若P1P2=8cm,则△PMN的周长是多少?
解:∵P1、P关于OA对称,P2、P关于OB对称,∴OA垂直平分P1P,OB垂直平分P2P.∴MP1=MP,NP2=NP.∴C△PMN=PM+MN+NP.=P1M+MN+NP2=P1P2=8cm.
1.从课后习题中选取;2.完成练习册本课时的习题。
数学八年级上册13.1.1 轴对称优秀习题ppt课件: 这是一份数学八年级上册<a href="/sx/tb_c102678_t3/?tag_id=26" target="_blank">13.1.1 轴对称优秀习题ppt课件</a>,共8页。PPT课件主要包含了复习巩固,综合运用等内容,欢迎下载使用。
人教版(2024)八年级上册第十三章 轴对称13.2 画轴对称图形13.2.1 作轴对称图形试讲课课件ppt: 这是一份人教版(2024)八年级上册<a href="/sx/tb_c88604_t3/?tag_id=26" target="_blank">第十三章 轴对称13.2 画轴对称图形13.2.1 作轴对称图形试讲课课件ppt</a>,共20页。PPT课件主要包含了新课导入,导入课题,学习目标,推进新课,巩固练习,练习1填空,对称点,垂直平分,对称轴,随堂演练等内容,欢迎下载使用。
人教版八年级上册第十三章 轴对称13.1 轴对称13.1.1 轴对称精品习题ppt课件: 这是一份人教版八年级上册<a href="/sx/tb_c102678_t3/?tag_id=26" target="_blank">第十三章 轴对称13.1 轴对称13.1.1 轴对称精品习题ppt课件</a>,共8页。PPT课件主要包含了复习巩固,综合运用等内容,欢迎下载使用。













