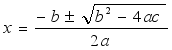初中数学人教版九年级上册21.2.2 公式法公开课教案

教

学

目

标

知识

目标

1.会用公式法解一元二次方程，理解用根的判别式判别根的情况及求相关的字母的取值范围.
 

能力

目标

1.经历推导求根公式的过程，加强推理技技能训练，进一步发展逻辑思维能力.体验类比、转化、降次的数学思想方法.

情感

目标

1.数学的新知都是建立在已有的知识基础之上，养成探究的能力，感受数学的奥秘.

教学

重点

推导求根公式的过程，理解根的判别式的作用．

教学

难点

熟练运用根的判别式解决根，字母系数的取值等相关问题.

教学环节

教学问题设计

师生活动

二次备课

创

设

情

景

【问题1】

　我们知道，任意一个一元二次方程都可以化为一般形式是：

  ax2+bx+c=0(a≠0)

你能用配方法求得它的解吗？

通过问题，激发学生对旧知的回忆.即配方法的一般步骤.

自

主

探

究

【问题2】.　用配方法解下列方程.

 ax2+bx+c=0(a≠0)

   解字母系数的方程是难点。

   教师可以引导这学生一起完成.让学生感受到特殊到一般的探究问题的方法.

移项 系数化1 .配方 降次    定解

同时一名学生板演展示.

教师问：方程右边的取值有哪些情况呢？从而方程的解的个数及解的情况又如何呢？说说你的想法.

给学生充分的思考，交流,展示之后。师生一起将三种情况展示在黑板上.从而给出公式法的定义，根的判别式,求根公式，一元二次方程的根的情况.

尝

试

应

用

1. 用公式法解下列方程

    (1)2x2-3x=0

   (2)5x+2=3x2

  (3)4x2+x+1=0

2.判断方程 x2-4x=-5的根的情况          

学生独立完成尝试部分，去熟悉用公式法解方程的步骤，应该注意的地方（必须先化为一般形式）.判断根的情况时不用解方程. 

注意：公式法解方程时，公式中的a,b,c分别是什么？

补

偿

提

高

1.若:x2+2x=m-1 没有实数根，

求证：x2+mx=1-2m

必有两个不相等的实数根.

[来源:Z*xx*k.Com][来源:Zxxk.Com]

本题是一道综合题目，首先根据根的判别式求得m的取值范围，然后再计算第二题的判别式，利用m的取值范围，得出判别式的范围大于0，从而得证。

注意字母系数.本题既考察了本节的知识，有运用了原来的不等式及上节的配方法。

小

结

1.通过本节课的学习你有什么收获？

2. 你还有哪些疑惑？

学生独立思考，师生梳理本课的知识点及方法

1.求根公式的推导过程.

2．用公式法解一元二次方程的一般步骤：先确定a、b、c的值、再算出判别式的值、最后代入求根公式求解．

3．用判别式判定一元二次方程根的情况.及求相关字母的取值范围.

    注意：字母系数。

作

业

必做：课本12页练习。

自主学习中的能力提升部分。

选做：自主学习中的拓展问题.

教师布置作业，并提出要求.

学生课下独立完成，延续课堂.

21.2.3解一元二次方程（公式法）教案

求根公式：