






高中人教A版 (2019)1.5 全称量词与存在量词背景图课件ppt
展开【问题1】我们如何对一个命题进行否定呢?一个命题和它的否定之间是什么关系呢?
一般地,对一个命题进行否定,就可以得到一个新的命题,这一新命题称为原命题的否定.
空集是集合A={1,2,3}的真子集
空集不是集合A={1,2,3}的真子集
结论:一个命题和它的否定不能同时为真命题,也不能同时为假命题,只能是一真一假,即原命题和它的否定之间真假相对.
【探究1】 写出下列命题的否定:(1)所有的矩形都是平行四边形;(2)每一个素数都是奇数;(3) .
【问题2】(1)这三个命题是什么类型的命题? 它们的否定是什么类型的命题?
存在一个矩形不是平行四边形
(2)如何对全称量词命题进行否定?
①将自然语言中的“所有的”“任意一个”等全称量词变为“并非所有的”“并非任意一个”等短语即可;
【结论1】全称量词命题的否定
解:(1)该命题的否定:存在一个能被3整除的整数不是奇数;
(2)该命题的否定:存在一个四边形,它的四个顶点不在同一个圆上;
【探究2】 写出下列命题的否定:(1)存在一个实数的绝对值是正数;(2)有些平行四边形是菱形;(3) .
每一个平行四边形都不是菱形
【问题3】(1)这三个命题是什么类型的命题? 它们的否定是什么类型的命题?
所有实数的绝对值都不是正数
(2)如何对存在量词命题进行否定?
①将自然语言中的“存在一个”“至少有一个”“有些”等存在量词,变为“不存在一个”“没有一个”等短语即可;
不存在一个实数,它的绝对值是正数
没有一个平行四边形是菱形
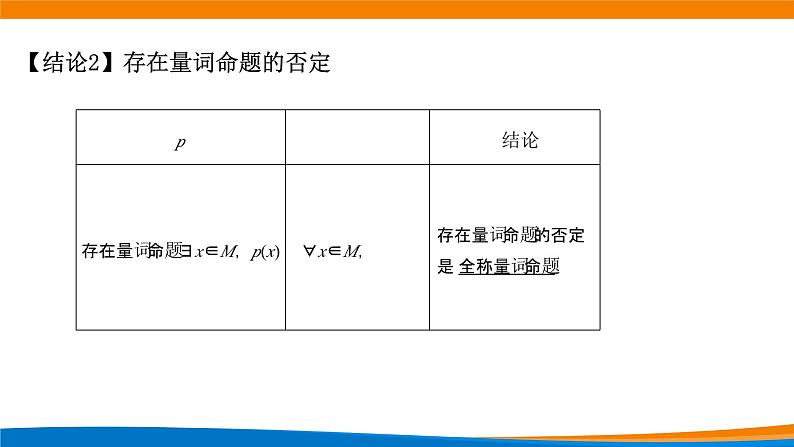
【结论2】存在量词命题的否定
【例2】写出下列存在量词命题的否定: (1) ; (2)有的三角形是等边三角形; (3)有一个偶数是素数.
(2)该命题的否定:所有的三角形都不是等边三角形;
(3)该命题的否定:任意一个偶数都不是素数.
【问题4】 (1)用自然语言描述的全称量词命题或存在量词命题的否定形式唯一吗?
答案: 不唯一,如“所有的菱形都是平行四边形”,它的否定是“并不是所有的菱形都是平行四边形”,也可以是“有些菱形不是平行四边形”;“有一个偶数是素数”,它的否定是“没有一个偶数是素数”,也可以是“所有的偶数都不是素数”
【问题4】 (2)对省略了量词的命题怎样否定?
答案: 对于含有一个量词的命题,容易知道它是全称量词命题或存在量词命题.一般地,省略了量词的命题是全称量词命题,可加上“所有的”或“对任意”,它的否定是存在量词命题.反之,亦然.
例如:“正方形是平行四边形”,
可写成:“所有的正方形都是平行四边形”
进行否定可写成:“存在一个正方形不是平行四边形”
再例如:“正方形不都是平行四边形”,
等价于:“有的(存在)正方形不是平行四边形”
进行否定可写成:“所有的正方形都是平行四边形”
【例3】写出下列命题的否定,并判断真假: (1)任意两个等边三角形都相似; (2) .
解:(1)该命题的否定: 存在两个等边三角形,它们不相似;假命题;
1.写出下列命题的否定: (1) ; (2)任意奇数的平方还是奇数; (3) 每个平行四边形都是中心对称图形.
(2)该命题的否定:存在一个奇数,它的平方不是奇数;
(3)该命题的否定:存在一个平行四边形不是中心对称图形.
2.写出下列命题的否定: (1)有些三角形是直角三角形; (2)有些梯形是等腰梯形; (3)存在一个实数,它的绝对值不是正数.
解:(1)该命题的否定:所有三角形都不是直角三角形;
(2)该命题的否定:所有梯形都不是等腰梯形;
(3)该命题的否定:所有实数的绝对值都是正数.
总结:1.全称量词命题和存在量词命题的否定
2.对省略了量词的命题可补上量词后进行否定.
布置作业:教科书习题1.5 3,4,5,6.
高中数学1.5 全称量词与存在量词说课课件ppt: 这是一份高中数学1.5 全称量词与存在量词说课课件ppt,共33页。
高中数学人教A版 (2019)必修 第一册1.5 全称量词与存在量词课文课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册1.5 全称量词与存在量词课文课件ppt,共16页。PPT课件主要包含了符号简记为,以上命题有何关系,全称量词命题的否定,换量词否结论,存在量词命题的否定,假命题,真命题等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册第一章 集合与常用逻辑用语1.5 全称量词与存在量词教案配套课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册第一章 集合与常用逻辑用语1.5 全称量词与存在量词教案配套课件ppt,共31页。PPT课件主要包含了目标认知,px,a≤0等内容,欢迎下载使用。













