新教材2023年高中数学第七章随机变量及其分布列章末知识梳理课件新人教A版选择性必修第三册

这是一份新教材2023年高中数学第七章随机变量及其分布列章末知识梳理课件新人教A版选择性必修第三册，共35页。

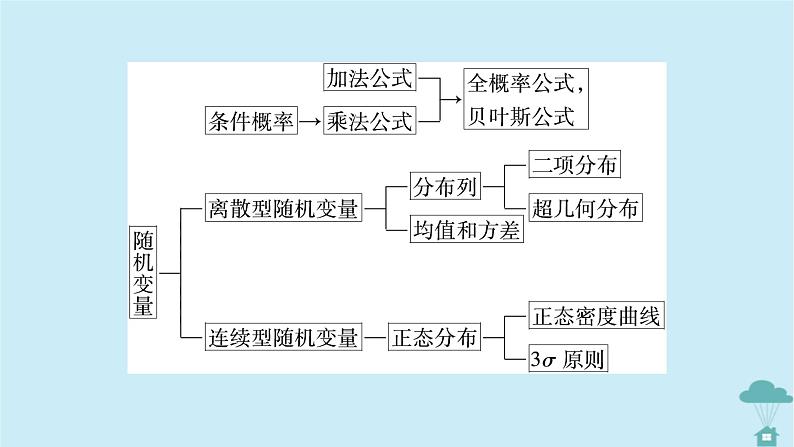
第七章　随机变量及其分布列章末知识梳理知识结构•理脉络 要点梳理•晰精华知识点1提示：不是．这是对全概率公式的形式主义的认识，完全把它作为一个“公式”来理解是不对的．其实，我们没有必要去背这个公式，根据B＝BΩ＝BA1＋BA2＋…＋BAn，应着眼于A1，A2，…，An的结构．随机变量知识点2提示：①两点分布是一种特殊的二项分布，即n＝1时的二项分布．②超几何分布与二项分布之间的关系：n次试验中，X为事件A出现的次数，当这n次试验是独立重复试验时，X服从二项分布；当这n次试验是不放回摸球，事件A为摸到某种特性(如某种颜色)的球时，X服从超几何分布．但是当袋子中的球的数目N很大时，超几何分布近似于二项分布，并且随着N的增加，这种近似的精确度也增加．③二项分布与超几何分布的区别：有放回抽样，每次抽取时的总体没有改变，因而每次抽到某物的概率都是相同的，可以看成是独立重复试验，此种抽样是二项分布模型．而不放回抽样，取出一个则总体中就少一个，因此每次取到某物的概率是不同的，此种抽样为超几何分布模型．因此，二项分布模型和超几何分布模型最主要的区别在于是有放回抽样还是不放回抽样．素养突破•提技能1．条件概率在高考命题中出现的概率较低，且多以选择题或填空题的形式出现，难度适中．2．计算在事件B发生的条件下事件A发生的概率，有两种方法：(1)利用条件概率的计算公式，分别计算概率P(AB)，P(B)，将它们相除即可；(2)利用缩小基本事件空间的方法计算，即将原来的基本事件空间Ω缩小为已知的条件事件B，原来事件A缩小为AB，每个基本事件发生的概率相等，从而利用古典概型的概率公式计算．在100件产品中，有95件合格品，5件不合格品，现从中不放回地取两次，每次任取1件产品．试求：(1)第一次取到不合格品的概率；(2)在第一次取到不合格品后，第二次再次取到不合格品的概率．[解析]　设第一次取到不合格品为事件A，第二次取到不合格品为事件B，则有：典例1(1)根据题设，事件B是由多个原因引起的，这多个原因分别为A1，A2，…，An；(2)利用全概率公式求出P(B)；(3)利用贝叶斯公式求出P(Ai|B)(i＝1，2，…，n)．在某次考试中，要从20道题中随机抽出6道题，若考生至少能答对其中4道题则可通过；若至少能答对其中5道题则获得优秀．已知某考生能答对其中10道题，并且知道他在这次考试中已经通过，求他获得优秀的概率．[解析]　设事件A为“该考生6道题全答对”，事件B为“该考生答对了其中5道题，另1道题答错”，事件C为“该考生答对了其中4道题，另2道题答错”，事件D为“该考生在这次考试中通过”，事件E为“该考生在这次考试中获得优秀”，则事件A，B，C两两互斥，且D＝A∪B∪C，E＝A∪B．典例2求离散型随机变量ξ的分布列、均值、方差的方法(1)理解离散型随机变量ξ的意义，写出ξ的所有可能取值；(2)求ξ取每个值的概率；(3)写出ξ的分布列；(4)根据均值、方差的定义求E(ξ)，D(ξ)．注意：如果ξ～B(n，p)，则E(ξ)＝np，D(ξ)＝np(1－p)．为创建文明城市，某城市号召出租车司机在高考期间至少进行一次“爱心送考”，该城市某出租车公司共200名司机，他们进行“爱心送考”的次数统计如图所示．典例3(1)求该出租车公司的司机进行“爱心送考”的人均次数；(2)从这200名司机中任选两人，设这两人进行“爱心送考”的次数之差的绝对值为随机变量X，求X的分布列及数学期望．[规律方法]　离散型随机变量的期望与方差的关注点(1)求离散型随机变量的期望与方差，一般先列出分布列，再按期望与方差的计算公式计算．(2)要熟记特殊分布的期望与方差公式(如两点分布、二项分布、超几何分布)．(3)注意期望与方差的性质．(4)实际应用问题，要注意分析实际问题用哪种数学模型来表达．本章的很多内容是由图表给出的，这实际上就是对数形结合思想的应用，数形结合思想在高考中占有重要位置，是高考重点考查的数学思想，它可以使题目的解答更形象、直观、一目了然．在一次测试中，测量结果X服从正态分布N(2，σ2)(σ>0)，若X在(0，2)内取值的概率为0.2，求：(1)X在(0，4)内取值的概率；(2)P(X>4)．典例4[分析]　本题考查正态分布，由于X服从正态分布N(2，σ2)(σ>0)，所以μ＝2.画出正态曲线的图象，根据图象性质求相应区间的概率．[解析]　(1)由X～N(2，σ2)知，图象的对称轴为直线x＝2，画出示意图，如图所示．[规律方法]　解决求某区间的概率问题，可以利用正态曲线的对称性，画出相应正态曲线的图象，应用数形结合思想把“求某一区间内的概率”问题转化为求“阴影部分面积”问题．分类讨论思想的实质：整体问题转化为部分问题来解决，转化成部分问题后增加了题设条件，易于解题．在求概率问题时，会经常遇到事件A是由多个互斥事件构成的情况(如“至少”“至多”型的概率问题)，随机变量ξ的某个取值可能对应着若干个试验结果的情形，这就需要借助分类讨论的思想方法将此类问题分成若干个小问题去解决．某电视台“挑战主持人”节目的挑战者闯第一关需要回答三个问题，其中前两个问题回答正确各得10分，回答不正确各得0分，第三个问题，回答正确得20分，回答不正确得－10分．如果一个挑战者回答前两题正确的概率都是0.8，回答第三题正确的概率为0.6，且各题回答正确与否相互之间没有影响．(1)求这位挑战者回答这三个问题的总得分X的分布列和数学期望；(2)求这位挑战者总得分不为负分(即X≥0)的概率．[分析]　解答本题的关键是明确ξ的取值及ξ取不同值时所表示的试验结果，明确ξ的取值后，利用相互独立事件的概率公式计算即可．典例5[解析]　(1)如果三个题目均答错，得0＋0＋(－10)＝－10(分)．如果三个题目均答对，得10＋10＋20＝40分．如果三个题目一对两错，包括两种情况：①前两个中一对一错，第三个错，得10＋0＋(－10)＝0(分)；②前两个错，第三个对，得0＋0＋20＝20(分)．如果三个题目两对一错，也包括两种情形：①前两个对，第三个错，得10＋10＋(－10)＝10(分)；②第三个对，前两个一对一错，得20＋10＋0＝30(分)．故ξ的可能取值为－10，0，10，20，30，40.E(X)＝－10×0.016＋0×0.128＋10×0.256＋20×0.024＋30×0.192＋40×0.384≈24.(2)这位挑战者总得分不为负分的概率为P(X≥0)＝1－P(X<0)＝1－0.016＝0.984.[规律方法]　此题应用了分类讨论思想，把总得分ξ的取值分情况进行讨论，而对ξ＝－10，40之外的值又分两种情况进行讨论，讨论一定要按一定标准，做到不重不漏．