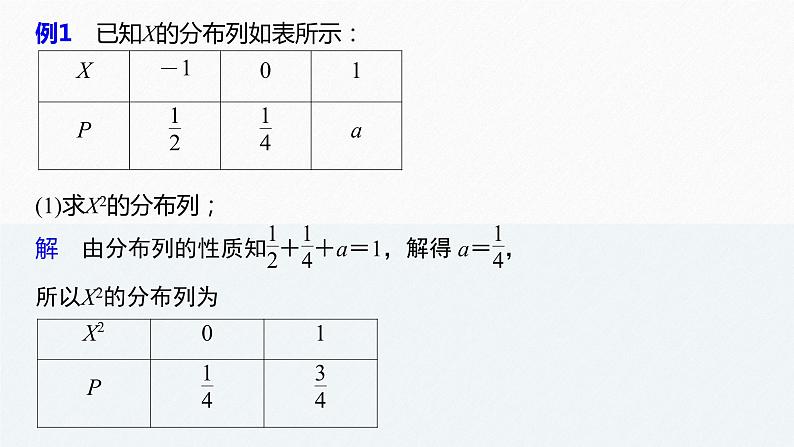
高中数学新教材选择性必修第三册课件+讲义 第7章 7.3.2 第2课时 离散型随机变量的方差的综合问题

这是一份高中数学新教材选择性必修第三册课件+讲义 第7章 7.3.2 第2课时 离散型随机变量的方差的综合问题，文件包含高中数学新教材选择性必修第三册第7章732第2课时离散型随机变量的方差的综合问题pptx、高中数学新教材选择性必修第三册第7章732第2课时离散型随机变量的方差的综合问题教师版docx、高中数学新教材选择性必修第三册第7章732第2课时离散型随机变量的方差的综合问题学生版docx等3份课件配套教学资源，其中PPT共60页， 欢迎下载使用。

高中数学新教材同步课件选择性必修第三册 高考政策|高中“新”课程，新在哪里?1、科目变化：外语语种增加，体育与健康必修。第一，必修课程，由国家根据学生全面发展需要设置，所有学生必须全部修习、全部考试。第二，选择性必修课程，由国家根据学生个性发展和升学考试需要设置。第三，选修课程，由学校根据实际情况统筹规划开设，学生自主选择修习。2、课程类别变化，必修课程、选择性必修课程将成为高考考查范围。在毕业总学分不变的情况下，对原必修课程学分进行重构，由必修课程学分、选择性必修课程学分组成，适当增加选修课程学分。3、学时和学分变化，高中生全年假期缩减到11周。4、授课方式变化，选课制度将全面推开。5、考试方式变化，高考统考科目由教育部命题，学业水平合格性、等级性考试由各省命题。第2课时　离散型随机变量的方差的综合问题第七章　7.3.2　离散型随机变量的方差1.掌握离散型随机变量的方差的性质.2.会用离散型随机变量的均值和方差解决一些实际应用问题.学习目标随堂演练课时对点练内容索引一、方差的性质二、方差的实际应用三、决策问题一、方差的性质例1　已知X的分布列如表所示：(1)求X2的分布列；所以X2的分布列为(2)计算X的方差；(3)若Y＝4X＋3，求Y的均值和方差.解　因为Y＝4X＋3，所以E(Y)＝4E(X)＋3＝2，D(Y)＝42D(X)＝11.反思感悟　求随机变量Y＝aX＋b方差的方法求随机变量Y＝aX＋b的方差，一种方法是先求Y的分布列，再求其均值，最后求方差；另一种方法是应用公式D(aX＋b)＝a2D(X)求解.跟踪训练1　设随机变量X的分布列为√若Y＝2X＋2，则D(Y)等于解析　由题意知，二、方差的实际应用例2　A，B两个投资项目的利润率分别为随机变量X1和X2，根据市场分析，X1和X2的分布列分别为(1)在A，B两个投资项目上各投资100万元，Y1和Y2分别表示投资项目A和B所得的利润，求方差D(Y1)，D(Y2)；解　根据题意，知Y1和Y2的分布列分别为则E(Y1)＝5×0.8＋10×0.2＝6，D(Y1)＝(5－6)2×0.8＋(10－6)2×0.2＝4，E(Y2)＝2×0.2＋8×0.5＋12×0.3＝8，D(Y2)＝(2－8)2×0.2＋(8－8)2×0.5＋(12－8)2×0.3＝12.(2)将x(0≤x≤100)万元投资项目A，(100－x)万元投资项目B，f(x)表示投资项目A所得利润的方差与投资项目B所得利润的方差的和.求f(x)的最小值，并指出x为何值时，f(x)取得最小值.当x＝75时，f(x)取得最小值3.反思感悟　随机变量的均值反映了随机变量取值的平均水平，方差反映了随机变量稳定于均值的程度，它们从整体和全局上刻画了随机变量，是生产实际中用于方案取舍的重要理论依据.一般先比较均值，若均值相同，再用方差来决定.跟踪训练2　甲、乙两个野生动物保护区有相同的自然环境，且野生动物的种类和数量也大致相等，而两个保护区内每个季度发生违反保护条例的事件次数的分布列分别为甲保护区：乙保护区：试评定两个保护区的管理水平.解　甲保护区的违规次数ξ的均值和方差分别为E(ξ)＝0×0.3＋1×0.3＋2×0.2＋3×0.2＝1.3，D(ξ)＝(0－1.3)2×0.3＋(1－1.3)2×0.3＋(2－1.3)2×0.2＋(3－1.3)2×0.2＝1.21.乙保护区的违规次数η的均值和方差分别为E(η)＝0×0.1＋1×0.5＋2×0.4＝1.3，D(η)＝(0－1.3)2×0.1＋(1－1.3)2×0.5＋(2－1.3)2×0.4＝0.41.因为E(ξ)＝E(η)，D(ξ)＞D(η)，所以两个保护区内每个季度发生的违规事件的平均次数相同，但甲保护区的违规事件次数相对分散和波动，乙保护区内的违规事件次数更集中和稳定.三、决策问题例3　某保险公司对一个拥有20 000人的企业推出一款意外险产品，每年每位职工只要交少量保费，发生意外后可一次性获得若干赔偿金，保险公司把企业的所有岗位共分为A，B，C三类工种，从事这三类工种的人数分别为12 000,6 000,2 000，由历史数据统计出三类工种的赔付频率如表(并以此估计赔付概率)：已知A，B，C三类工种的职工每人每年保费分别为25元、25元、40元，出险后的赔偿金额分别为100万元、100万元、50万元，保险公司在开展此项业务过程中的固定支出为每年10万元.(1)求保险公司在该业务所获利润的均值；解　设工种A，B，C职工的每份保单保险公司的收益为随机变量X，Y，Z，则X，Y，Z的分布列分别为保险公司所获利润的均值为12 000×15＋6 000×5－2 000×10－100 000＝90 000，所以保险公司在该业务所获利润的均值为9万元.(2)现有如下两个方案供企业选择：方案1：企业不与保险公司合作，职工不交保险，出意外企业自行拿出与保险公司提供的等额赔偿金赔偿付给意外职工，企业开展这项工作的固定支出为每年12万元；方案2：企业与保险公司合作，企业负责职工保费的70%，职工个人负责保费的30%，出险后赔偿金由保险公司赔付，企业无额外专项开支.请根据企业成本差异给出选择合适方案的建议.解　方案1：企业不与保险公司合作，则企业每年安全支出与固定开支共为方案2：企业与保险公司合作，则企业支出保险金额为(12 000×25＋6 000×25＋2 000×40)×0.7＝37.1×104.因为46×104>37.1×104，所以建议企业选择方案2.反思感悟　均值、方差在决策中的作用(1)均值：均值反映了离散型随机变量取值的平均水平，均值越大，平均水平越高.(2)方差：方差反映了离散型随机变量取值的离散波动程度，方差越大越不稳定.(3)在决策中常结合实际情形依据均值、方差做出决断.跟踪训练3　某投资公司对以下两个项目进行前期市场调研.项目A：通信设备.根据调研，投资到该项目上，所有可能结果为获利40%、亏损20%、不赔不赚，且这三种情况发生的概率分别为 a.项目B：新能源汽车.根据调研，投资到该项目上，所有可能结果为获利30%、亏损10%，且这两种情况发生的概率分别为b，c.经测算，当投入A，B两个项目的资金相等时，它们所获得的平均收益(即均值)也相等.(1)求a，b，c的值；设投到项目A，B的资金都为x万元，变量X1和X2分别表示投资项目A和B所获得的利润，则X1和X2的分布列分别为E(X2)＝0.3bx－0.1cx，因为E(X1)＝E(X2)，所以0.3bx－0.1cx＝0.2x，即0.3b－0.1c＝0.2. ①又b＋c＝1， ②(2)若将100万元全部投到其中一个项目，请你从投资回报稳定性的角度考虑，为投资公司选择一个合理的项目，并说明理由.解　选择项目B.理由如下：当投入100万元资金时，由(1)知x＝100，所以E(X1)＝E(X2)＝20，因为E(X1)＝E(X2)，D(X1)>D(X2)，说明虽然项目A和项目B的平均收益相等，但项目B更稳妥，所以从风险回报稳定性的角度考虑，建议该投资公司选择项目B.1.知识清单：(1)方差的性质.(2)方差的实际应用.2.方法归纳：转化化归.3.常见误区：公式计算错误.课堂小结随堂演练1.已知随机变量X满足D(X)＝2，则D(3X＋2)等于A.6 B.8 C.18 D.201234√解析　∵D(X)＝2，∴D(3X＋2)＝9D(X)＝18.2.已知随机变量ξ满足P(ξ＝1)＝0.3，P(ξ＝2)＝0.7，则E(ξ)和D(ξ)的值分别为A.0.6和0.7 B.1.7和0.09C.0.3和0.7 D.1.7和0.211234√解析　E(ξ)＝1×0.3＋2×0.7＝1.7，D(ξ)＝(1－1.7)2×0.3＋(2－1.7)2×0.7＝0.21.则当p在(0,1)内增大时，A.D(ξ)减小 B.D(ξ)增大C.D(ξ)先减小后增大 D.D(ξ)先增大后减小12343.设0＜p＜1，随机变量ξ的分布列为√1234解析　由分布列可知所以D(ξ)是关于p的二次函数，其图象开口向下，12344.随机变量ξ的分布列为1234课时对点练1.(多选)对于离散型随机变量X，有关它的均值E(X)和方差D(X)，下列说法正确的是A.E(X)是反映随机变量的平均取值B.D(X)越小，说明X越集中于E(X)C.E(aX＋b)＝aE(X)＋bD.D(aX＋b)＝a2D(X)＋b基础巩固12345678910111213141516√√√解析　离散型随机变量的均值反映了随机变量取值的平均水平，方差反映了随机变量取值偏离于均值的平均程度，方差越小，说明随机变量的取值越集中于均值，即A，B正确；由均值和方差的性质可得，E(aX＋b)＝aE(X)＋b，D(aX＋b)＝a2D(X)，即C正确，D错.123456789101112131415162.若随机变量X服从两点分布，且成功的概率p＝0.5，则E(X)和D(X)分别为A.0.5和0.25 B.0.5和0.75C.1和0.25 D.1和0.7512345678910111213141516√解析　∵X服从两点分布，∴X的分布列为∴E(X)＝0×0.5＋1×0.5＝0.5，D(X)＝0.52×0.5＋(1－0.5)2×0.5＝0.25.已知随机变量Y＝aX＋b(a>0)且E(Y)＝10，D(Y)＝4，则a与b的值为A.a＝10，b＝3 B.a＝3，b＝10C.a＝5，b＝6 D.a＝6，b＝53.若随机变量X的分布列为12345678910111213141516√解析　因为0.2＋m＝1，所以m＝0.8，所以E(X)＝0×0.2＋1×0.8＝0.8，D(X)＝0.2×0.8＝0.16.因为E(Y)＝10，D(Y)＝4，所以E(Y)＝aE(X)＋b＝0.8a＋b＝10， ①D(Y)＝a2D(X)＝0.16a2＝4， ②由①②，解得a＝5，b＝6，故选C.123456789101112131415164.已知0D(2ξ2－1)C.E(2ξ1－1)>E(2ξ2－1)，D(2ξ1－1)E(2ξ2－1)，D(2ξ1－1)>D(2ξ2－1)√12345678910111213141516解析　由均值与方差的性质，可知E(aξ＋b)＝aE(ξ)＋b，D(aξ＋b)＝a2D(ξ)，则E(2ξi－1)＝2E(ξi)－1，D(2ξi－1)＝4D(ξi).12345678910111213141516所以E(ξ1)>E(ξ2)，D(ξ1)>D(ξ2)，所以E(2ξ1－1)>E(2ξ2－1)，D(2ξ1－1)>D(2ξ2－1)，故选D.1234567891011121314151616.为了解与掌握一些基本的地震安全防护知识，某小学在9月份开学初对全校学生进行了为期一周的知识讲座，事后并进行了测试(满分100分)，根据测试成绩评定为“合格”(60分以上包含60分)、“不合格”两个等级，同时对相应等级进行量化：“合格”定为10分，“不合格”定为5分.现随机抽取部分学生的答卷，统计结果及对应的频率分布直方图如图所示.12345678910111213141516(1)求a，b，c的值；12345678910111213141516解　由频率分布直方图可知，得分在[20,40)的频率为0.005×20＝0.1，又由频率分布直方图可知，得分在[80,100]的频率为0.2，所以b＝60×0.2＝12.又6＋a＋24＋b＝60，得a＋b＝30，所以a＝18.12345678910111213141516(2)用分层随机抽样的方法，从评定等级为“合格”和“不合格”的学生中抽取10人进行座谈，再从这10人中任选4人，记所选4人的量化总分为ξ，求ξ的分布列及均值E(ξ)；12345678910111213141516解　“合格”与“不合格”的人数比例为36∶24＝3∶2，因此抽取的10人中“合格”有6人，“不合格”有4人，所以ξ的可能取值为40,35,30,25,20.12345678910111213141516故ξ的分布列为12345678910111213141516(3)设函数f(ξ)＝ (其中D(ξ)表示ξ的方差)是评估安全教育方案成效的一种模拟函数.当f(ξ)≥2.5时，认定教育方案是有效的，否则认定教育方案应需调整，试以此函数为参考依据.在(2)的条件下，判断该校是否应调整安全教育方案？12345678910111213141516解　由(2)可得故可以认为该校的安全教育方案是无效的，需要调整安全教育方案.