浙教版九年级上册3.4 圆心角优秀ppt课件

导入新课

创设情景，引出课题

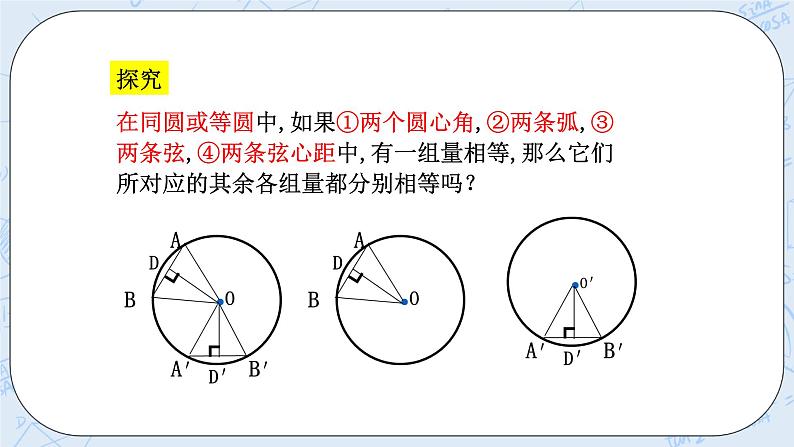
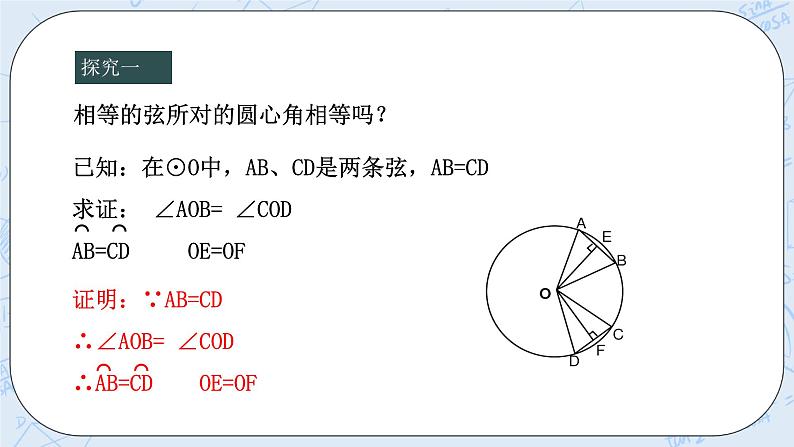
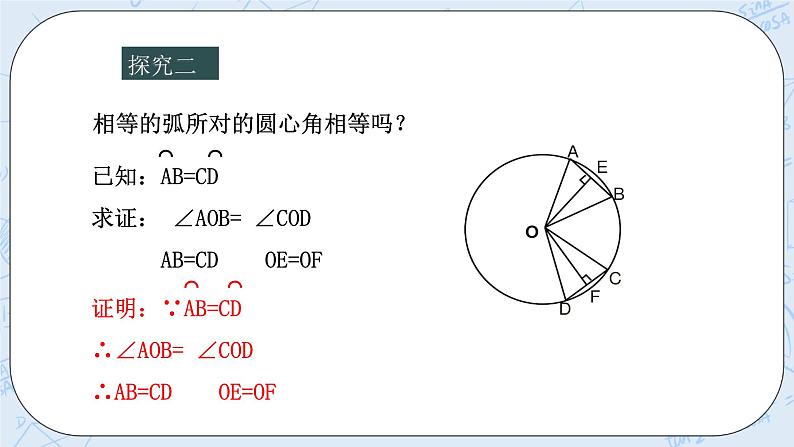
提出并找出条件与结论

圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.

提出问题：圆心角定理的逆定理能成立吗？

探究

在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等吗？

探究一：相等的弦所对的圆心角相等吗？

已知：在⊙O中，AB、CD是两条弦，AB=CD

求证： ∠AOB= ∠COD

AB=CD     OE=OF

证明：∵AB=CD

∴∠AOB= ∠COD

∴AB=CD    OE=OF

探究二

相等的弧所对的圆心角相等吗？

已知：弧AB=弧CD    

求证： ∠AOB= ∠COD   AB=CD   OE=OF

证明：

∵弧AB=弧CD

∴∠AOB= ∠COD

∴AB=CD    OE=OF

探究3

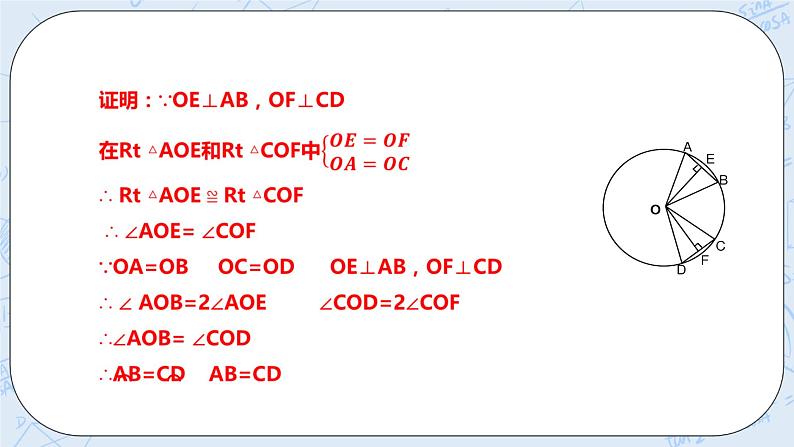
相等的弦心距所对的圆心角,弦,弧相等吗？    

已知：在⊙O中，AB、CD是两条弦，OE⊥AB，OF⊥CD垂足为E、F，OE=OF

求证： ∠AOB= ∠COD

弧AB=弧CD     AB=CD

证明：∵OE⊥AB，OF⊥CD

在Rt △AOE和Rt △COF中

∴ Rt △AOE ≌ Rt △COF     

 ∴ ∠AOE= ∠COF

∵OA=OB     OC=OD      OE⊥AB，OF⊥CD

∴ ∠ AOB=2∠AOE         ∠COD=2∠COF

∴∠AOB= ∠COD

∴弧AB=弧CD    AB=CD

二、提炼概念

结论

在同圆或等圆中，如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等，那么它们所对应的其余的各组量都相等.

思考

自议

通过理解圆的旋转不变性，理解圆心角定理的逆定理；

转化思想，把圆心角、弧、弦、弦心距利用圆心角定理的逆定理进行互相转化．

讲授新课

三、典例精讲

例3  如图，等边三角形ABC内接于⊙O,连结OA,OB,OC．延长AO,分别交BC于点P，交BC于点D，连结BD,CD.判断四边形BDCO是哪一种特殊四边形，并说明理由.

解：四边形BDCO是菱形，理由如下：

∵AB=BC=CA   ∴∠AOB=∠BOC=∠COA=120°

∴∠BOD=180°-∠AOB=60°

同理：∠COD=60°

又∵OB=OD

∴OB=OD=BD

同理：OC=CD

∴OB=OC=BD=CD

∴四边形BDCO是菱形

例4 已知：如图，△ABC为等边三角形，以AB为直径的⊙O分别交AC，BC于点D，E．求证：AD=DE=EB.

解: 连结OD,OE

在等边三角形ABC中，∠A=60°

∵OA=OD ∴△AOD为等边三角形

∴∠AOD=60°  同理∠BOE=60°

∴∠DOE= 180°-∠AOD-∠BOE=60°

∴∠DOE= ∠AOD=∠BOE

∴AD= DE=EB

在同圆或等圆中，证明角相等，可以证明角所对的弧相等．

在同圆或等圆中，要证明圆心角、弧、弦、弦心距这四组量中的某一组量相等，通常是转化成证明另外三组量中的某一组量相等．

课堂检测

四、巩固训练

1．下列说法中正确的是     (　   　)

   A．相等的弦所对的弧相等

   B．相等的圆心角所对的弧相等

   C．在同一个圆中相等的弧所对的弦相等

   D．相等的弦所对的圆心角相等

答案：C

2．观察下列选项中的图及相应推理，其中正确的是 (　  )

A                        B

C                        D

答案：  B

【解析】 A错误，是因为两弧不是在同圆或等圆中；B正确，∵＝，∴＋＝＋，∴＝，∴CD＝AB；C错误，∠AOB＝×360°＝40°；D错误，当MN是AE的垂直平分线时，才有＝.

   3.如图所示，已知⊙O中的弦AB＝CD.

求证：(1)＝；

(2)    ∠AOC＝∠BOD.

证明：(1)∵AB＝CD，

∴＝(在同一圆中，如果两条弦相等，那么这两条弦所对的弧相等)．

∴－＝－.

∴＝.

(2)∵＝，

∴∠AOC＝∠BOD(在同一圆中，如果两条弧相等，那么这两条弧所对的圆心角相等)．

4.如图所示，A，B，C为⊙O上的三点，且有＝＝，连结AB，BC，CA.

(1)试确定△ABC的形状；

(2)若AB＝a，求⊙O的半径．

解：(1)∵＝＝(已知)，

∴AB＝BC＝CA(在同圆中相等的弧所对的弦相等)，

∴△ABC为等边三角形．(2)连结OA，OB，OC，过O作OE⊥BC，垂足为E.

∵＝＝(已知)，

∴∠AOB＝∠BOC＝∠COA(在同圆中相等的弧所对的圆心角相等)．

又∵∠AOB＋∠BOC＋∠COA＝360°(周角的定义)，∴∠BOC＝120°，又∵OE⊥BC，

∴∠BOE＝∠COE＝60°，

BE＝EC＝BC＝AB＝a(等边三角形三线合一)．

∴∠OBE＝90°－∠BOE＝30°.

∴OE＝OB.

根据勾股定理则有BE2＋OE2＝OB2，

∴(a)2＋(OB)2＝OB2，

解得OB＝a(负值已舍)，即⊙O的半径为a.

课堂小结

圆心角定理的逆定理

在同圆或等圆中，如果______________、___________、__________、_____________中有一对量相等，那么它们所对应的其余各对量都相等．

说明：这个定理可以引导我们从多方面找出解决问题的方法，要解决弧相等的问题，可以从它们所对的弦、弦心距或所对的圆心角是否相等入手；要解决弦相等的问题，可以从它们所对的弧或所对的圆心角、弦心距是否相等入手．

两个圆心角，两条弧，两条弦，两个弦心距