






选择性必修 第一册1.2.3 直线与平面的夹角优质课件ppt
展开1.2.3 直线与平面的夹角(1)
本节课选自《2019人教B版高中数学选择性必修第一册》第一章《空间向量与立体几何》,本节主要学习直线与平面的夹角。学生在学习了异面直线所成角的概念,对空间角的问题有了一定的经验,线面角的问题,依然按照将空间问题化为平面问题、将立体几何问题化为空间向量运算问题的基本思路展开。为培养学生直观想象、数学抽象、逻辑推理、数学建模和数学运算的核心素养提供舞台。
课程目标 | 学科素养 |
A..掌握直线在平面内的射影及斜线与平面所成角的概念. B.理解最小角定理及公式cos θ=cos θ1cos θ2,并能利用这一公式解决相关问题. C.会利用空间向量求直线与平面所成的角问题. | 1.数学抽象:线面角的定义 2.逻辑推理:最小角定理 3.直观想象:线面角的几何模型 4.数学运算:用空间向量求直线与平面所成的角问题 |
1.教学重点:利用空间向量求直线与平面所成的角问题.
2.教学难点:线面角的概念
多媒体
教学过程 | 教学设计意图 核心素养目标 |
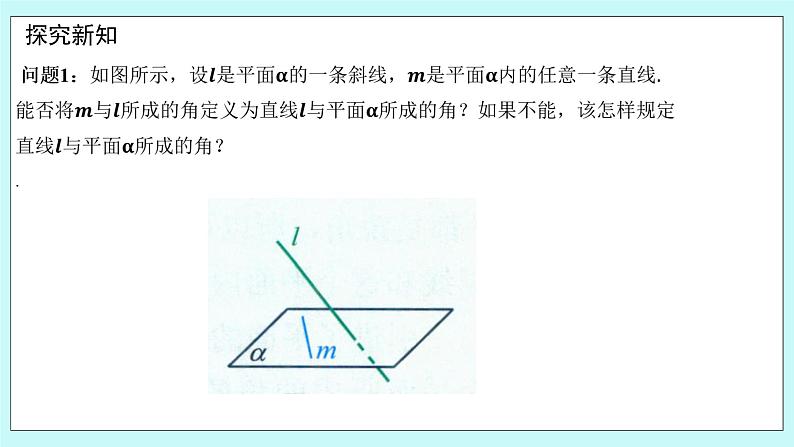
一、情境导学 日常生活中,很多场景中都有直线与平面成一定角度的形象,例如如图1所示,握笔写字时,如果把笔抽象成直线,把纸抽象成平面,则直线与平面呈一定角度;如图2所示,地球仪的地轴(即旋转轴)与赤道所在的平面垂直,并且与水平桌面呈一定角度,那么怎样来刻画直线与平面所成的角呢? 二、探究新知 问题1:如图所示,设是平面的一条斜线,是平面内的任意一条直线. 能否将与所成的角定义为直线与平面所成的角?如果不能,该怎样规定直线与平面所成的角?
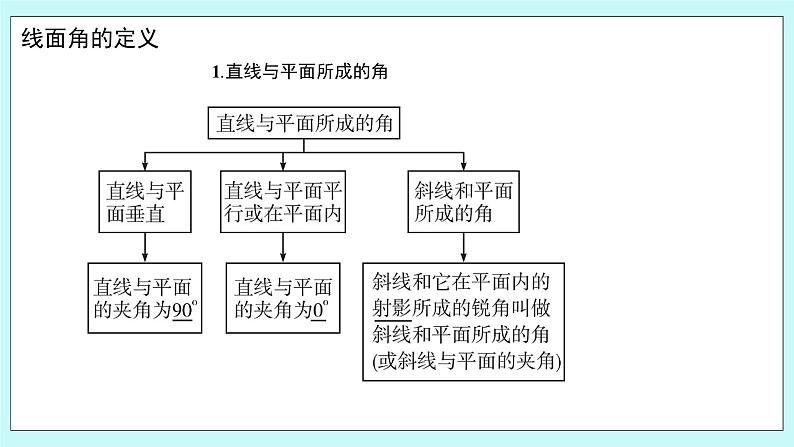
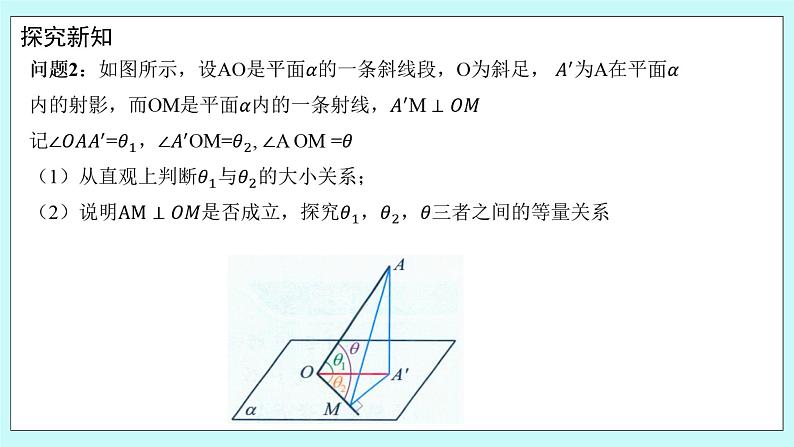
1.直线与平面所成的角 1.判断 (1)直线与平面所成的角就是该直线与平面内的直线所成的角. ( ) (2)若直线与平面相交,则该直线与平面所成角的范围为0,. ( ) 答案:(1)× (2)× 2.直线与平面的夹角的取值范围是什么?斜线与平面的夹角的取值范围是什么? 提示:直线与平面的夹角的取值范围是,斜线与平面的夹角的取值范围是. 问题2:如图所示,设AO是平面的一条斜线段,O为斜足, 为A在平面内的射影,而OM是平面内的一条射线,M 记=,OM=, A OM = (1)从直观上判断与的大小关系; (2)说明是否成立,探究,,三者之间的等量关系
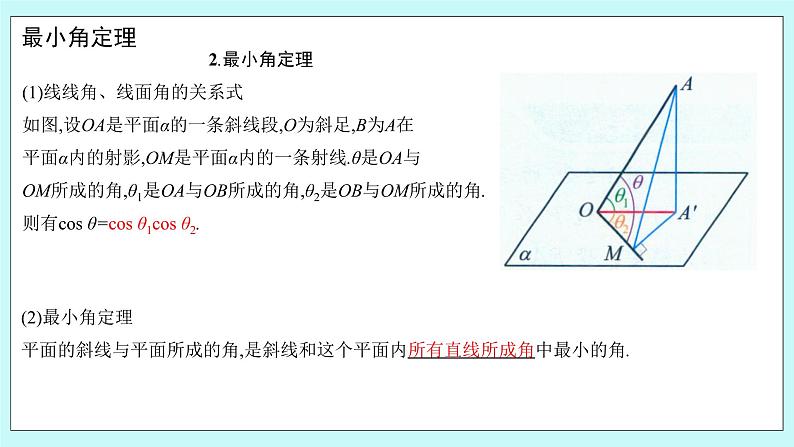
2.最小角定理 (1)线线角、线面角的关系式 如图,设OA是平面α的一条斜线段,O为斜足,B为A在 平面α内的射影,OM是平面α内的一条射线.θ是OA与 OM所成的角,θ1是OA与OB所成的角,θ2是OB与OM所成的角. 则有cos θ=cos θ1cos θ2. (2)最小角定理 平面的斜线与平面所成的角,是斜线和这个平面内所有直线所成角中最小的角.
3. 已知平面α内的角∠APB=60°,射线PC与PA,PB所成角均为135°,则PC与平面α所成角的余弦值是( ) A.- B. C. D.- 解析:设PC与平面α所成的角为θ,由最小角定理知cos 45°=cos θcos 30°,∴cos θ=. 答案:B 4.将公式cos θ=cos θ1cos θ2中角的余弦值换成正弦值是否成立? 提示:不成立.只有在特定的条件下能相等.也只能是数值上的相等,不具有等式的一般性结论. 问题3:如果 是直线的一个方向向量, 是平面的一个法向量,设直线与平面所成角的大小为,通过作图讨论与的关系 3.用空间向量求直线与平面的夹角 如果v是直线l的一个方向向量,n是平面α的一个法向量,设直线l与平面α所成角的大小为θ,则有 (1)θ=-<v,n>,θ=<v,n>-; (2)cos θ=sin<v,n>,sin θ=|cos<v,n>|. 5.判断:直线与平面所成的角等于直线的方向向量与该平面法向量夹角的余角.( ) 答案:× 例1 已知是正方体,求与平面所成角的大小。
解:(方法一)以D为原点, ,,的方向分别为轴正方向,正方体的棱长为单位长度,建立如图所示直角坐标系, 则: 所以=(0,1,-1), =(-1,0,0) , =(1,1,0) , 设平面的一个法向量为, 则取=1,可得, 又因为=== 所以=. 与平面所成角的大小为: - = (方法二)设B的中点为E,连接 如图所示, 因为是正方形, 所以. 又因为,且, 所以再根据 B=,可知 因此在面内的射影为, 所以E就是与平面所成的角, 因为正方体中有=,所以在Rt中, E= , 又因为E是一个锐角,所以E=, 与平面所成角的大小为 求线面角 1.利用定义法求直线与平面所成的角,首先要作出斜线和这条斜线在平面内的射影所成的锐角,然后通过解三角形求出直线与平面所成的角的大小.其基本步骤可归纳为“一作,二证,三计算”. 2.找射影的两种方法:(1)斜线上任一点在平面内的射影必在斜线在平面内的射影上;(2)利用已知垂直关系得出线面垂直,确定射影. 3.本例中找出点E在平面BCD中的射影是解决问题的核心,对于几何体中缺少棱长等数据信息,可根据几何体的特征进行假设,这样处理不影响角度问题. 跟踪训练1 如图所示,在直四棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAD=90°,AB= ,,BC=1,AD=AA1=3. (1)证明:AC⊥B1D; (2)求直线B1C1与平面ACD1所成角的正弦值.
(1)证明:以A为原点,以的方向分别 为x轴,y轴,z轴的正方向建立空间直角坐标系, 则A(0,0,0),C(,1,0),B1(,0,3), D(0,3,0),C1(,1,3),D1(0,3,3). 易知=(,1,0),=(-,3,-3), ∴=0,∴AC⊥B1D. (2)解:设平面ACD1的法向量为m=(x,y,z), =(,1,0),=(0,3,3), 则令x=1, 则y=-,z=, ∴平面ACD1的一个法向量为m=(1,-). 设直线B1C1与平面ACD1所成的角为θ, ∵=(0,1,0), ∴sin θ=, ∴直线B1C1与平面ACD1所成角的正弦值为. 例2 正四面体ABCD,CD在平面α内,点E是线段AC的中点,在该四面体绕CD旋转的过程中,直线BE与平面α所成的角θ不可能是 ( ) A.0 B. C. D. 解析:直线BE与CD所成角的余弦值为,线面角是直线与平面内的直线所成角的最小值,即线线角≥线面角,则cos θ≥,代入选项验证,得角θ不可能是.故选D. 答案:D
反思感悟 1.最小角定理是立体几何的重要定理之一,指与平面斜交的直线与它在该平面内的射影的夹角不大于直线与平面内其他直线的夹角.图形语言表示如下: 线线角≥线面角 2.本例中先明确直线BE与CD所成角的余弦值是突破口,再利用线线角≥线面角这一结论,即可做出判断. 跟踪训练2 PA、PB、PC是由P点出发的三条射线,两两夹角均为60°,则直线PC与平面PAB所成角的余弦值是( ) A. B. C. D. 解析:设所求角为θ,根据最小角定理及公式可得cos 60°=cos 30°·cos θ,得cos θ=. 答案:C |
创设问题情境,引导学生体会数学问题源于生活,经历发现问题,分析问题和解决问题的过程。 提升学生数学抽象,逻辑推理和数学建模的核心素养。
由问题引导,让学生感受和理解线面角的定义,感受实现立体几何问题向平面几何转化的思想方法。
通过对线面角的向量表示的学习,进而线面角问题,转化为向量坐标化运算,让学生感受,用代数方法解问题决立体几何问题。发展学生逻辑推理,数学抽象和数学运算的核心素养。
通过典型例题的分析和解决,让学生感受空间向量坐标运算在解决空间几何中的应用。发展学生数学抽象、逻辑推理的核心素养。
通过典例解析,进一步让学生体会空间向量坐标在解决立体几何中的应用,提升推理论证能力,提高学生的数学运算及逻辑推理的核心素养。
|
三、达标检测 1.已知向量m,n分别是直线l的方向向量和平面α的法向量,若cos<m,n>= - ,则l与α所成的角为( ) A.30° B.60° C.120° D.150° 解析:设l与α所成的角为θ且θ∈[0,90°],则sin θ=|cos<m,n>|= .∴θ=30°.答案:A 2.AB⊥平面α于点B,BC为AC在α内的射影,CD在α内,若∠ACD=60°,∠BCD=45°,则AC和平面α所成的角为( ) A.90° B.60° C.45° D.30° 解析:设AC和平面α所成的角为θ,则cos 60°=cos θcos 45°,故cos θ=,所以θ=45°.答案:C 3.在三棱锥P-ABC中,AB⊥BC,AB=BC=PA,点O,D分别是AC,PC的中点,OP⊥底面ABC,则直线OD与平面PBC所成角的正弦值为( ) A. B. C. D. 解析:以O为原点,射线OA,OB,OP为x,y,z轴建立空间直角坐标系,如图, 设AB=a,则OP=a=a,则D-a,0,a ,P0,0,a,B0,a,0,C-a,0,0. =-a,-a,0,=0,a,-a. 可求得平面PBC的法向量为n=, ∴cos<,n>=, 设与平面PBC所成的角为θ, 则sin θ=,故选D. 答案:D 4.等腰直角△ABC的斜边AB在平面α内,若AC与α成30°角,则斜边上的中线CM与平面α所成的角为 . 答案:45° 5.如图所示,ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=1,AD=,求CS与平面ABCD所成的角的正弦值. 解: 是平面ABCD的法向量, 设的夹角为φ,CS与平面ABCD的夹角为θ. ∵, ∴·()==1. ||=1,||==, ∴cos φ=. ∴sin θ=|cos φ|=. ∴CS与平面ABCD所成角的正弦值为. |
通过练习巩固本节所学知识,通过学生解决问题,发展学生的数学运算、逻辑推理、数学建模的核心素养。
|
四、小结 五、课时练 |
通过总结,让学生进一步巩固本节所学内容,提高概括能力。 |
教学中主要突出了几个方面:一是创设问题情景,通过现实情境提出问题,让学生初步体会数学问题源于生活,并以此来激发学生的探究心理。二是注重概念教学,让学生经历感知、分析、抽象、推理论证的过程,发展学生核心素养。三是典例解析,通过对典型问题的分析解决,帮助学生建立运用空间向量解决立体几何问题的基本思路。教学设计尽量做到注意学生的心理特点和认知规律,触发学生的思维,使教学过程真正成为学生的学习过程,以思维教学代替单纯的记忆教学。注意在探究问题时留给学生充分的时间, 使数学教学成为数学活动的教学。从而发展学生的直观想象、逻辑推理、数学建模的核心素养。
高中数学人教B版 (2019)选择性必修 第一册1.2.3 直线与平面的夹角完整版ppt课件: 这是一份高中数学人教B版 (2019)选择性必修 第一册1.2.3 直线与平面的夹角完整版ppt课件,文件包含人教B版高中数学选择性必修第一册123《直线与平面的夹角》课件ppt、人教B版高中数学选择性必修第一册123《直线与平面的夹角》学案doc、人教B版高中数学选择性必修第一册123《直线与平面的夹角》课后素养落实含答案doc等3份课件配套教学资源,其中PPT共60页, 欢迎下载使用。
高中数学人教B版 (2019)选择性必修 第一册第一章 空间向量与立体几何1.2 空间向量在立体几何中的应用1.2.3 直线与平面的夹角试讲课ppt课件: 这是一份高中数学人教B版 (2019)选择性必修 第一册第一章 空间向量与立体几何1.2 空间向量在立体几何中的应用1.2.3 直线与平面的夹角试讲课ppt课件,文件包含人教B版高中数学选择性必修第一册123《直线与平面的夹角2》课件pptx、人教B版高中数学选择性必修第一册123《直线与平面的夹角2》教学设计docx等2份课件配套教学资源,其中PPT共31页, 欢迎下载使用。
人教B版 (2019)选择性必修 第一册1.2.3 直线与平面的夹角示范课课件ppt: 这是一份人教B版 (2019)选择性必修 第一册1.2.3 直线与平面的夹角示范课课件ppt,共41页。













