初中数学沪科版八年级上册15.4 角的平分线评优课课件ppt

这是一份初中数学沪科版八年级上册15.4 角的平分线评优课课件ppt，共20页。PPT课件主要包含了CONTENTS，学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业，怎样作出角的平分线等内容，欢迎下载使用。

1.掌握角的平分线的画法. 2.掌握角的平分线的性质. （重点）
知识点1 角的平分线的画法
角的平分线的画法1：通过折纸可以作出一个角的角平分线.在半透明纸上任画一个角，请你用折叠的方法，找出角的平分线，如图.
角的平分线的画法2：也可以用量角器来画一个角的平分线.角的平分线的画法3：下面介绍用尺规作图的方法作出∠AOB的平分线（如图）.
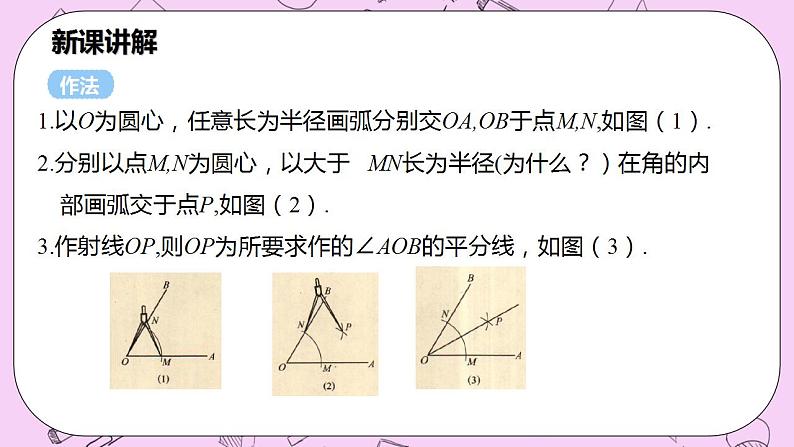
1.以O为圆心，任意长为半径画弧分别交OA,OB于点M,N,如图（1）.2.分别以点M,N为圆心，以大于 MN长为半径(为什么？）在角的内 部画弧交于点P,如图（2）.3.作射线OP,则OP为所要求作的∠AOB的平分线，如图（3）.
1.根据作图，你能证明所作射线OP,就是∠AOB的平分线吗？2.当∠AOB的两边成一直线时（即∠AOB= 180°），你会作 这个角的平分线吗？这时的角平分线与直线AB是什么关系？
过一点作已知直线的垂线：1.经过已知直线上的一点作这条直线的垂线： 如图所示，已知直线AB和AB上一点C，作AB的垂线，使它经过点C. 作法：如图所示． 第一步：作平角ACB的平分线CF； 第二步：反向延长射线CF.直线CF就是所要求作的垂线．
2．经过已知直线外一点作这条直线的垂线： 如图所示，已知直线AB和AB外一点C， 作AB的垂线，使它经过点C. 作法：如图所示． 第一步：以点C为圆心，作能与AB相交于D 、 E两点的弧； 第二步：作∠ DCE的平分线CF； 第三步：反向延长射线CF.则直线CF就是所要求作的垂线．
1.如图所示，已知∠AOB， 求作：∠AOM＝ ∠AOB. 导引：要作射线OM，使∠AOM＝ ∠AOB， 可作 ∠AOB的平分线．
解：作法：(1)以点O为圆心，适当长为半径画弧，交OA于点E，交OB于点F；(2)分别以点E，F为圆心，大于 EF的长为半径画弧，两弧在∠AOB的内部交于点C；(3)画射线OC；(4)同理，作∠AOC的平分线OM. ∠AOM即为所求(如图所示)．
知识点2 角的平分线的性质
PD长度间有什么关系吗？
如图，OP是∠AOB的平分线，P是OP上的任一点，过点P分别作PC⊥OA,PD ⊥ OB,点C,D是垂足.你能猜想PC，PD长度间有什么关系吗？证明你的猜想.
下面我们给出上面“思考”中猜想结论的证明.证明：∵OP平分∠AOB，（已知） ∴∠AOP=∠BOP.(角平分线定义） 又 ∵ PC⊥OA，PD ⊥ OB，（已知） ∴∠PCO=∠PDO= 90°.(垂直的定义） 在△PCO 和△ PDO中， ∵ ∴ △ PCO≌ △ PDO.(AAS)∴ PC=PD.
角的平分线的性质：角平分线上的点到角两边的距离相等． 要点精析：(1)点一定要在角平分线上；(2)点到角两边的距离 是指点到角两边垂线段的长度；(3)角平分线的性质可用来证 明两条线段相等．
1.如图，在△ABC中，∠C＝90°，BC＝AC，AD是∠BAC的平分线，DE⊥AB于点E.若AB＝10 cm，求△DBE的周长． 导引：要求△DBE的周长，实质是求BE＋DE＋BD的长，而题中已知 AB＝10 cm，因此需证DE＋BD＝AE，又AD是角平分线及垂直条件知DE＝CD，所以需证BC＝AE，由BC＝AC，因此只需证 AC＝AE，它可由Rt△ACD≌Rt△AED得出．
解：∵AD平分∠CAB，且∠C＝90°，DE⊥AB， ∴DC＝DE. 又∵∠C＝∠DEA＝90°，AD＝AD， ∴Rt△ACD≌Rt△AED，∴AC＝AE. 又∵AC＝BC， ∴AC＝AE＝BC. ∴DE＋EB＋BD＝DC＋EB＋BD＝BC＋EB＝AE＋EB＝AB. 又∵AB＝10 cm， ∴△DBE的周长为DB＋BE＋DE＝10 cm.
2.如图，OC是∠AOB的平分线，P是OC上一点，PD⊥OA于点D，PD＝6，则点P到边OB的距离为(　　)A．6 B．5 C．4 D．3