数学6.2 排列与组合教学演示课件ppt

这是一份数学6.2 排列与组合教学演示课件ppt，共21页。PPT课件主要包含了排列的概念，相应的排法，N3×26，故有6种不同的选法，不同排法如下图所示，读作n的阶乘法，排列数的计算，排列的应用，课堂练习，排队问题等内容，欢迎下载使用。

问题1、要从甲、乙、丙3名同学中选出2名参加某天的一项活动，其中1名同学参加上午的活动，1名同学参加下午的活动，有多少种不同的方法？
上 午 下 午
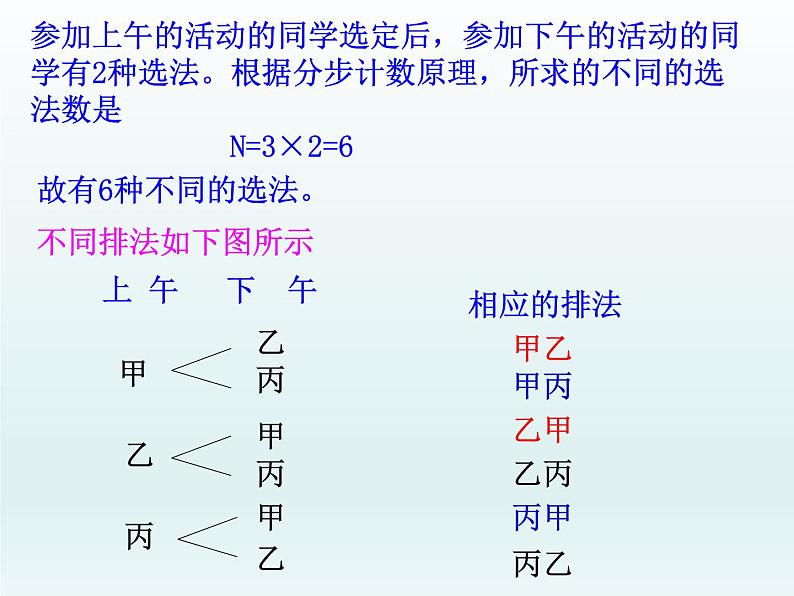
参加上午的活动的同学选定后，参加下午的活动的同学有2种选法。根据分步计数原理，所求的不同的选法数是
问题2 从a,b,c,d 这4个字母中,每次取出3个按顺序排成一列，共有多少种不同的排法？
根据分步计数原理，所求的不同的排法数是
4 ×3 ×2=24 (种）
一般地，从n个不同中取出m 个元素 ，按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列。
1、元素不能重复。n个中不能重复，m个中也不能重复。
2、“按一定顺序”就是与位置有关，这是判断一个问题是否是排列问题的关键。
3、两个排列相同，当且仅当这两个排列中的元素完全相同，而且元素的排列顺序也完全相同。
4、m＜n时的排列叫选排列，m＝n时的排列叫全排列。
例1、下列问题中哪些是排列问题？
（1）10名学生中抽2名学生开会
（2）10名学生中选2名做正、副组长
（3）从2,3,5,7,11中任取两个数相乘
（4）从2,3,5,7,11中任取两个数相除
（5）20位同学互通一次电话
（6）20位同学互通一封信
问题1可看作甲、乙、丙3取2的排列问题：共3×2=6种方法
问题2可看作a,b,c,d中4取3的排列问题：共4×3×2=24种方法
例1、 1、某年全国足球甲A联赛共有14个队参加，每队要与其余各队在主、客场分别比赛一次，共进行多少场比赛？
2、（1）从5本不同的书中选3本送给3名同学，每人各一本，共有多少种不同的送法？
（2）从5种不同的书中买3本送给3名同学， 每人各一本，共有多少种不同的送法？
1、从4种蔬菜品种中选出3种，分别种植在不同土质的3块土地上进行试验，有　　种不同的种植方法？
2、从参加乒乓球团体比赛的5名运动员中选出3名进行某场比赛，并排定他们的出场顺序，有　　种不同的方法？
例2、（数字问题）用0-9这10个数字（1）可以组成多少个三位数？
（3）可以组成多少个无重复数字的三位奇数？
（2）可以组成多少个无重复数字的三位数？
点评方法：对于特殊元素或特殊位置， 通常优先安排.
练习、用0，1，2，3，4，5这6个数字（1）能组成多少个无重复数字的六位数？（2）能组成多少个无重复数字的四位偶数？（3）能组成多少个比1325大的四位数.
例3、3名男生，4名女生，按照不同的要求排队， 求不同的排法种数
（1）选5名同学站成一排
（2）前排2人，后排3人
例3、3名男生，4名女生，按照不同的要求排队
（5）全体站成一排，若甲、乙必须在两端
（3）若甲男生不站排头，也不站排尾
（4）甲只能站在排头或排尾，有多少种方法？
（6）甲不站在排头，乙不站在排尾， 有多少种排法？
（7）全体站成一排，男生不相邻
（8）全体站成一排，男，女生各不相邻
插空法：对于不相邻问题，先将允许相邻的元素排列，然后再进行插入.
（9）全体站成一排，男生站在一起
（10）全体站成一排，男、女生各站在一起
（11）全体站成一排，甲、乙之间必须有2人.
捆绑法：对于相邻问题，可以把相邻元素看成一个整体，当成一个元素和其他元素进行排列