












高中数学人教A版 (2019)选择性必修 第三册6.2 排列与组合获奖课件ppt
展开1.通过实例理解排列的概念.2.能应用排列知识解决简单的实际问题.3.通过学习排列的概念,进一步提升数学抽象及逻辑推理素养
“排列三”是中国福利彩票的一种,它是使用摇奖机、摇奖球进行摇奖的,“排列三”,“排列五”共同摇奖,一次摇出5个号码,“排列三”的中奖号码为当期摇出的全部中奖号码的前3位,“排列五”的中奖号码为当期摇出的全部中奖号码,每日进行开奖.
福彩3D即“排列三”摇出的号码的总的结果数是多少?提示 以第1位数为例,第1位的奖号是从0到9这10个数字中摇出一个,每个数字都有相同概率摇出,所以第1位上就有10种可能,同理第2位、第3位都各有10种可能,前3位总共就有1 000种组合方法.
问题1 从甲、乙、丙3名同学中选出2名参加一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有几种不同的选法?
上午 下午 相应的选法
我们把上面问题中被取出的对象叫做元素.
上述问题就是从3个不同的元素中任取2个,按照一定的顺序排成一列,求一共有多少种不同的排法.
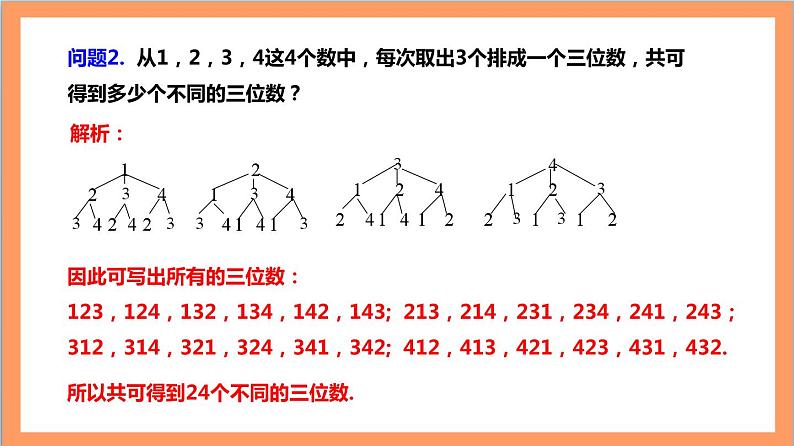
问题2. 从1,2,3,4这4个数中,每次取出3个排成一个三位数,共可得到多少个不同的三位数?
因此可写出所有的三位数:123,124,132,134,142,143; 213,214,231,234,241,243;312,314,321,324,341,342; 412,413,421,423,431,432.
所以共可得到24个不同的三位数.
上面问题1、2有什么共同特征?
答:上面三个问题都是研究从一些不同元素中取出部分元素,并按照一定的顺序排成一列的方法数.
一般地,从n个不同元素中取出m (m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
定义中包含两个基本内容:
判断一个问题是否是排列的标志
1.元素不能重复,n个元素中不能重复,m个元素中也不能重复.
2.“按一定顺序”,就是与位置有关,这是判断一个问题是否是排列问题的关键.
3.两个排列相同,当且仅当这两个排列中的元素完全相同,而且元素的排列顺序也完全相同.
例1 某省中学生足球预选赛每组有6支队,每支队都要与同组的其他各队在主、客场分别比赛1场,那么每组共进行多少场比赛?
分析:每组任意2支队之间进行的1场比赛,可以看作是从该组6支队中选取2支,按“主队、客队”的顺序排成的一个排列.解:先从这6支队中选1支为主队,然后从剩下的5支队中选1支为客队,按照分步乘法计数原理,每组进行的比赛场数为:6x5=30
例2 (1)一张餐桌上有5盘不同的菜,甲、乙、丙3名同学每人从中各取1盘菜,共有多少种不同的取法?
可以先从这5盘菜中取1盘给同学甲,然后从剩下的4盘菜中取1盘给同学乙,最后从剩下的3盘菜中取1盘给同学丙.按分步乘法计数原理,共有5 x 4 x 3 = 60 种不同的取法.
(2)学校食堂的一个窗口共卖5种菜,甲、乙、丙3名同学每人从中选一种,共有多少种不同的选法?
可以先让同学甲从5种菜中选1种,有5种选法;再让同学乙从5种菜中选1种,也有5种选法;最后让同学丙从5种菜中选1种,同样有5种选法.根据分步乘法计数原理,不同的选法种数为 5 x 5 x 5 = 125
1.(1)用0到4这5个自然数组成的没有重复数字的全部两位数。解:4×4=16(2)从a,b,c,d中取出2个字母的所有排列。解:4×3=12
2.一位老师要给4个班轮流做讲座,每个班讲1场,有多少种轮流次序?解:4×3×2×1=243.学校乒乓团体比赛采用5场3胜制(5场单打),每支球队派3名运动员参赛,前3场比赛每名运动员各出场1次,其中第1,2位出场的运动员在后2场比赛中还将各出场1次。(1)从5名运动员中选3名参加比赛,前3场比赛有几种出场情况? 解:5×4×3=60
(2)甲、乙、丙3名运动员参加比赛,写出所有可能的出场情况。解:①比3场结束,有甲乙丙,甲丙乙,乙甲丙,乙丙甲,丙甲乙,丙乙甲6种情况;②比4场结束,有甲乙丙甲,甲乙丙乙,甲丙乙甲,甲丙乙丙,乙丙甲乙,乙丙甲丙,乙甲丙甲,乙甲丙乙,丙甲乙丙,丙甲乙甲,丙乙甲丙,丙乙甲乙12种情况;③比5场结束,有甲乙丙甲乙,甲乙丙乙甲,甲丙乙甲丙,甲丙乙丙甲,乙甲丙乙甲,乙甲丙甲乙,乙丙甲乙丙,乙丙甲丙乙,丙甲乙丙甲,丙甲乙甲丙,丙乙甲丙乙,丙乙甲乙丙共12种。
1.(多选)下面问题中,不是排列问题的是A.由1,2,3三个数字组成无重复数字的三位数B.从40人中选5人组成篮球队C.从100人中选2人抽样调查D.从1,2,3,4,5中选2个数组成集合
解析 选项A中组成的三位数与数字的排列顺序有关,选项B,C,D只需取出元素即可,与元素的排列顺序无关.
2.从甲、乙、丙三人中选两人站成一排的所有站法为A.甲乙、乙甲、甲丙、丙甲B.甲乙丙、乙丙甲C.甲乙、甲丙、乙甲、乙丙、丙甲、丙乙D.甲乙、甲丙、乙丙
解析 从三人中选出两人,而且要考虑这两人的顺序,所以有如下6种站法:甲乙、甲丙、乙甲、乙丙、丙甲、丙乙.
3.从5本不同的书中选两本送给2名同学,每人一本,则不同的送书方法的种数为A.5 B.10 C.20 D.60
解析 不同的送书种数为5×4=20.
7.从1,2,3,4这4个数字中选出3个数字构成无重复数字的三位数有____个.
4.有8种不同的菜种,任选4种种在不同土质的4块地里,有_______种不同的种法.
解析 将4块不同土质的地看作4个不同的位置,从8种不同的菜种中任选4种种在4块不同土质的地里,则本题即为从8个不同元素中任选4个元素的排列问题,所以不同的种法共有8×7×6×5=1 680(种).
5.某信号兵用红、黄、蓝3面旗从上到下挂在竖直的旗杆上表示信号,每次可以任挂1面、2面或3面,并且不同的顺序表示不同的信号,则一共可以表示______种不同的信号.解析 第1类,挂1面旗表示信号,有3种不同方法;第2类,挂2面旗表示信号,有3×2=6(种)不同方法;第3类,挂3面旗表示信号,有3×2×1=6(种)不同方法.根据分类加法计数原理,可以表示的信号共有3+6+6=15(种).答案 15
1.排列的基本概念:一般地,从n个不同的元素中取出m(m≤n)个元素,并按照一定的顺序排成一列,叫做从n个不同的元素中取出m个元素的一个排列2.排列问题种要完成“一件事情”包含两个基本步骤:一是取出元素;二是按一定顺序排列
高中数学人教A版 (2019)选择性必修 第三册7.5 正态分布优质课课件ppt: 这是一份高中数学人教A版 (2019)选择性必修 第三册<a href="/sx/tb_c4000360_t3/?tag_id=26" target="_blank">7.5 正态分布优质课课件ppt</a>,文件包含75《正态分布》课件-人教版高中数学选修三pptx、75《正态分布》分层作业原卷版-人教版高中数学选修三docx、75《正态分布》分层作业解析版-人教版高中数学选修三docx等3份课件配套教学资源,其中PPT共27页, 欢迎下载使用。
数学选择性必修 第三册第六章 计数原理6.2 排列与组合完整版课件ppt: 这是一份数学选择性必修 第三册<a href="/sx/tb_c4000352_t3/?tag_id=26" target="_blank">第六章 计数原理6.2 排列与组合完整版课件ppt</a>,文件包含624《组合数》课件-人教版高中数学选修三pptx、624《组合数》分层作业原卷版-人教版高中数学选修三docx、624《组合数》分层作业解析版-人教版高中数学选修三docx等3份课件配套教学资源,其中PPT共25页, 欢迎下载使用。
高中数学人教A版 (2019)选择性必修 第三册6.2 排列与组合试讲课课件ppt: 这是一份高中数学人教A版 (2019)选择性必修 第三册<a href="/sx/tb_c4000352_t3/?tag_id=26" target="_blank">6.2 排列与组合试讲课课件ppt</a>,文件包含623《组合》课件-人教版高中数学选修三pptx、623《组合》分层作业原卷版-人教版高中数学选修三docx、623《组合》分层作业解析版-人教版高中数学选修三docx等3份课件配套教学资源,其中PPT共18页, 欢迎下载使用。













