初中数学人教版九年级上册23.2.2 中心对称图形优秀当堂检测题

人教版数学九年级上册压轴题专题精选汇编

专题12 中心对称图形

考试时间：120分钟 试卷满分：100分

一．选择题（共10小题，满分20分，每小题2分）

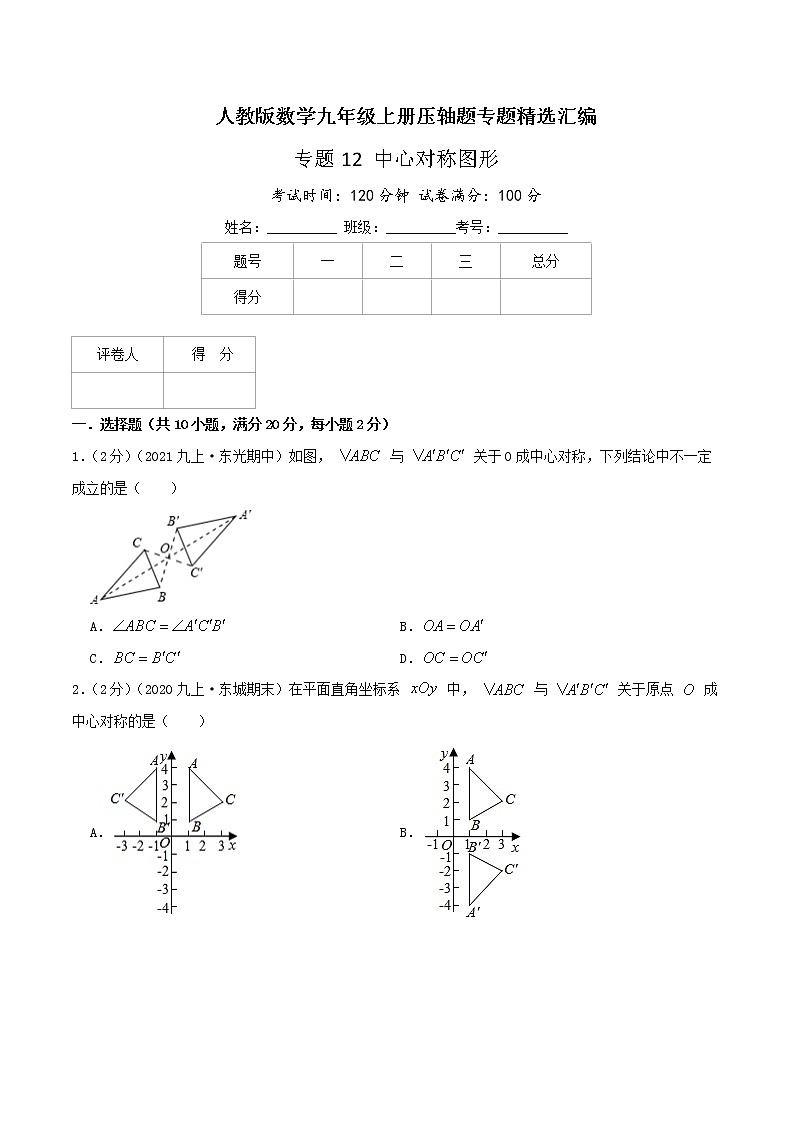
1．（2分）（2021九上·东光期中）如图， 与 关于O成中心对称，下列结论中不一定成立的是（　　） 

A． B．

C． D．

【答案】A

【完整解答】解：∵对应点的连线被对称中心平分，

∴ ， ，

即B、D符合题意，

∵成中心对称图形的两个图形是全等形，

∴对应线段相等，

即 ，

∴C符合题意，

故答案为：A．

【思路引导】先求出 ， ，再求出 ，最后判断即可。

2．（2分）（2020九上·东城期末）在平面直角坐标系 中， 与 关于原点 成中心对称的是（　　） 

A． B．

C． D．

【答案】D

【完整解答】解：A、△ABC与△A'B'C'关于y轴对称，所以A选项不符合题意；

B、△ABC与△A'B'C'关于x轴对称，所以B选项不符合题意；

C、△ABC与△A'B'C'关于（- ，0）对称，所以C选项不符合题意；

D、△ABC与△A'B'C'关于原点对称，所以D选项符合题意；

【思路引导】根据中心对称图形的定义逐项判断即可。

3．（2分）（2021九上·西安期末）矩形具有而菱形不一定具有的性质是（　　）  

A．中心对称图形 B．对边分别相等

C．对角线互相平分 D．对角线相等

【答案】D

【完整解答】解：矩形具有而菱形不一定具有的性质是对角线相等，

故答案为：D.

【思路引导】根据矩形和菱形的性质进行判断即可得出答案.

4．（2分）（2020九上·福州月考）如图， 是一个中心对称图形的一部分，O点是对称中心，点A和点B是一对对应点， ，那么将这个图形补成一个完整的图形是（　　） 

A．矩形 B．菱形 C．正方形 D．梯形

【答案】A

【完整解答】解：如图，

∵O点是对称中心，△A′B′C′是△ABC关于点O的对称图形，

∴AC′=BC，BC′=AC，

∴四边形ACBC′是平行四边形，

∵∠C=90°，

∴平行四边形ACBC′是矩形．

故答案为：A．

【思路引导】根据中心对称的性质得出AC′=BC，BC′=AC，利用两组对边分别相等可证四边形ACBC′是平行四边形，由∠C=90°，可证平行四边形ACBC′是矩形．

5．（2分）（2017九上·平桥期中）如图，将△ABC绕点C（0，﹣1）旋转180°得到△A'B'C，设点A的坐标为（a，b），则点A'的坐标为（　　） 

A．（﹣a，﹣b） B．（﹣a，﹣b﹣1）

C．（﹣a，﹣b+1） D．（﹣a，﹣b﹣2）

【答案】D

【完整解答】如图，

把AA′向上平移1个单位得A的对应点A1坐标为（a，b+1）．

因A1、A2关于原点对称，所以A′对应点A2（﹣a，﹣b﹣1），∴A′（﹣a，﹣b﹣2）．

故答案为：D．

【思路引导】把AA′向上平移1个单位，根据平移的性质及点的坐标的平移规律得A的对应点A1坐标，根据关于坐标原点对称的点，横坐标互为相反数，纵坐标也互为相反数，由A1的坐标即可得出A2的坐标，再根据点的坐标的平移规律得A2的对应点A'坐标.

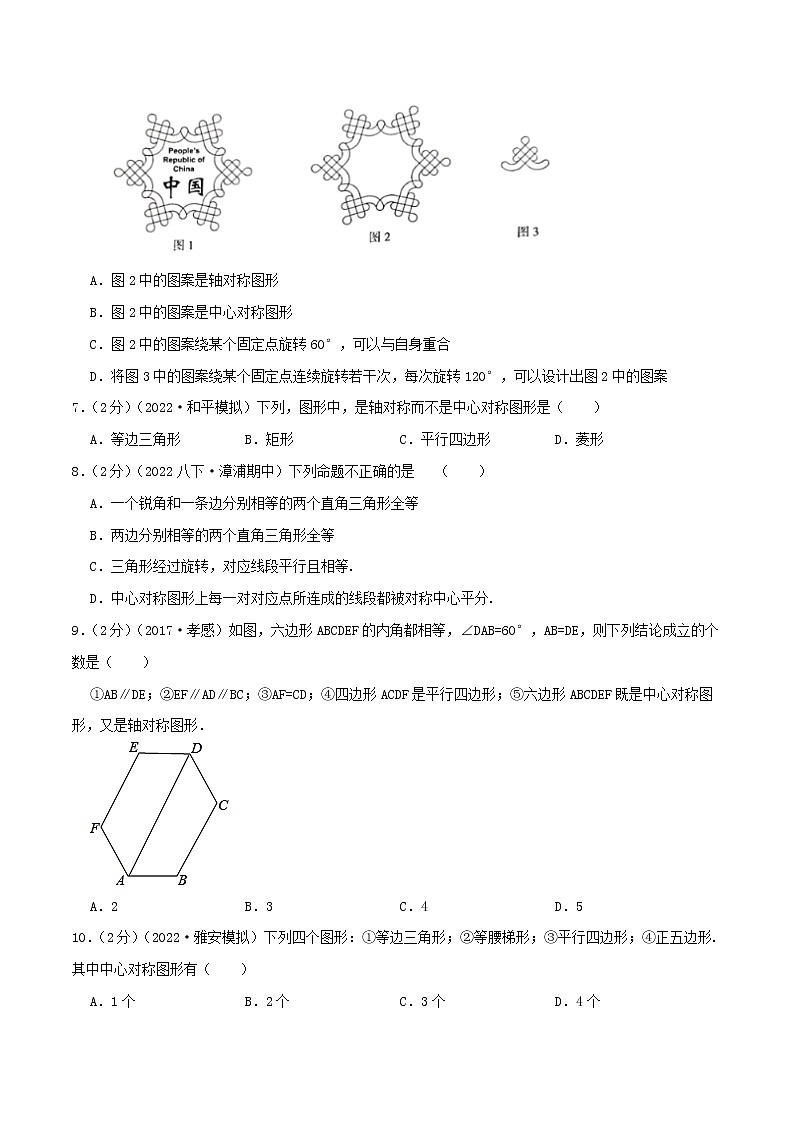
6．（2分）（2022八下·漳州期末）北京2022年冬奥会的开幕式上，各个国家和地区代表团入场所持的引导牌是中国结和雪花融合的造型，如图1是中国体育代表团的引导牌，观察发现，图2中的图案可以由图3中的图案经过对称、旋转等变换得到.下列关于图2和图3的说法中，不正确的是（　　）

A．图2中的图案是轴对称图形

B．图2中的图案是中心对称图形

C．图2中的图案绕某个固定点旋转60°，可以与自身重合

D．将图3中的图案绕某个固定点连续旋转若干次，每次旋转120°，可以设计出图2中的图案

【答案】D

【完整解答】解：

如图，图2中的图案是轴对称图形，也是中心对称图形，故A、B正确；

这3条对称轴将图2平均分成了六份，其中每份所占的圆心角的度数为

图2中的图案绕对称轴的交点旋转60°，可以与自身重合，故C正确；

将图3中的图案绕某个固定点连续旋转若干次，每次旋转120°，不能设计出图2中的图案，故D错误.

故答案为：D.

【思路引导】把一个平面图形沿着某一条直线折叠，直线两旁的部分能完全重合的几何图形就是轴对称图形；把一个图形绕着某一点旋转180°后能与其自身重合的图形就是中心对称图形，据此可判断A、B；根据图2可知图形被平分成6份，利用360°除以6可得旋转的度数，据此判断C；若每次旋转120°，则旋转三次可绕城一周，据此判断D.

7．（2分）（2022·和平模拟）下列，图形中，是轴对称而不是中心对称图形是（　　）

A．等边三角形 B．矩形 C．平行四边形 D．菱形

【答案】A

【完整解答】解：A．是轴对称图形，不是中心对称图形，符合题意；

B．是轴对称图形，也是中心对称图形，不符合题意；

C．不是轴对称图形，是中心对称图形，不符合题意；

D．是轴对称图形，也是中心对称图形，不符合题意．

故答案为：A．

【思路引导】弄清轴对称图形和中心对称图形区别与联系是关键。

8．（2分）（2022八下·漳浦期中）下列命题不正确的是   （　　）

A．一个锐角和一条边分别相等的两个直角三角形全等

B．两边分别相等的两个直角三角形全等

C．三角形经过旋转，对应线段平行且相等.

D．中心对称图形上每一对对应点所连成的线段都被对称中心平分.

【答案】C

【完整解答】解：A、一个锐角和一条边分别相等再加上两个直角是相等角，用ASA或AAS可证明两三角形全等，故此选项正确，不符合题意；

B、若是一条直角边一条斜边分别相等，则用HL证明全等；若是两条直角边分别相等，则用SAS证明全等，因此两边分别相等的两个直角三角形全等，故此选项正确，不符合题意；

C、三角形经过旋转，对应线段相等但不一定平行，故此选项错误，符合题意；

D、中心对称图形上每一对对应点所连成的线段都被对称中心平分，是中心对称图形的性质，故此选项正确，不符合题意.

故答案为：C.

【思路引导】由直角三角形中两直角相等，加上一个锐角和一条边对应相等，符合ASA或AAS判定三角形全等，即可判断A选项；一直角边和一斜边对应相等，符合HL判定定理，两条直角边分别对应相等加直角对应相等，符合SAS判定全等，即可判断B选项；根据旋转前后图形形状和大小不变可知，对应线段相等但不一定平行，可判断C选项；根据中心对称图形的性质，对应点连成的线段都被对称中心平分，即可判断D选项.

9．（2分）（2017·孝感）如图，六边形ABCDEF的内角都相等，∠DAB=60°，AB=DE，则下列结论成立的个数是（　　）

①AB∥DE；②EF∥AD∥BC；③AF=CD；④四边形ACDF是平行四边形；⑤六边形ABCDEF既是中心对称图形，又是轴对称图形．

A．2 B．3 C．4 D．5

【答案】D

【完整解答】解：∵六边形ABCDEF的内角都相等，

∴∠EFA=∠FED=∠FAB=∠ABC=120°，

∵∠DAB=60°，

∴∠DAF=60°，

∴∠EFA+∠DAF=180°，∠DAB+∠ABC=180°，

∴AD∥EF∥CB，故②正确，

∴∠FED+∠EDA=180°，

∴∠EDA=∠ADC=60°，

∴∠EDA=∠DAB，

∴AB∥DE，故①正确，

∵∠FAD=∠EDA，∠CDA=∠BAD，EF∥AD∥BC，

∴四边形EFAD，四边形BCDA是等腰梯形，

∴AF=DE，AB=CD，

∵AB=DE，

∴AF=CD，故③正确，

连接CF与AD交于点O，连接DF、AC、AE、DB、BE．

∵∠CDA=∠DAF，

∴AF∥CD，AF=CD，

∴四边形AFDC是平行四边形，故④正确，

同法可证四边形AEDB是平行四边形，

∴AD与CF，AD与BE互相平分，

∴OF=OC，OE=OB，OA=OD，

∴六边形ABCDEF既是中心对称图形，故⑤正确，

故选D．

【思路引导】根据六边形ABCDEF的内角都相等，∠DAB=60°，平行线的判定，平行四边形的判定，中心对称图形的定义一一判断即可．

10．（2分）（2022·雅安模拟）下列四个图形：①等边三角形；②等腰梯形；③平行四边形；④正五边形.其中中心对称图形有（　　） 

A．1个 B．2个 C．3个 D．4个

【答案】A

【完整解答】解：根据中心对称图形的定义可以判断③平行四边形是中心对称图形；①等边三角形、②等腰梯形、④正五边形均不是中心对称图形，

故答案为：A.

【思路引导】中心对称图形：在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形.

二．填空题（共10小题，满分20分，每小题2分）

11．（2分）（2022八下·拱墅期中）如图是一个中心对称图形，A为对称中心，若 ， ， ，则 的长为　     　.

【答案】12

【完整解答】解： 在 中， ， ，

，

∵B与B'关于A中心对称，

.

故答案为：12.

【思路引导】在直角三角形ABC中，根据30度角所对的直角边等于斜边的一半得AB=2AC，然后根据中心对称的性质得BB'=2AB可求解.

12．（2分）（）已知点A（-1，2）与点B（3，4）是成中心对称的图形上的两个对称点，则对称中心的坐标为　         　。

【答案】（1，3）

【完整解答】解：设对称中心为（x，y），
∴x==1，y==3，
∴对称中心的坐标为 （1，3）.
故答案为： （1，3） .

【思路引导】根据中点坐标公式分别求出对称中心的横纵坐标，即可解答.

13．（2分）（）在方格纸中，选择标有序号①、②、③、④中的一个小正方形涂黑，能与图中阴影部分构成中心对称图形的小正方形的序号是　     　。

【答案】②

【完整解答】解：根据中心对称图形的特点可知， ② 符合条件.
故答案为： ② .

【思路引导】中心对称图形绕其中心点旋转180°后图形仍和原来图形重合，依此特点分别判断即可.

14．（2分）（2021九上·互助期中）如图，△DEC与△ABC关于点C成中心对称，AB＝3，AC＝1，∠D＝90°，则AE的长是　     　．

【答案】

【完整解答】 与 关于点C成中心对称

故答案为： .

【思路引导】利用全等三角形的性质以及勾股定理即可得到答案。

15．（2分）（2021九上·鼓楼月考）如图，△ABC和△DEC关于点C成中心对称，若AC＝1，AB＝2，∠BAC＝90°，则AE的长是　     　.

【答案】2

【完整解答】解：∵△DEC与△ABC关于点C成中心对称，

∴△ABC≌△DEC，

∴AB＝DE＝2，AC＝DC＝1，∠D＝∠BAC＝90°，

∴AD＝2，

∵∠D＝90°，

∴AE＝ .

故答案为： .

【思路引导】由题意可得△ABC≌△DEC，则AB＝DE＝2，AC＝DC＝1，∠D＝∠BAC＝90°，求出AD的值，然后利用勾股定理就可得到AE.

16．（2分）（2019九上·望城期中）如图，△ABC中，∠C＝90°，AC＝6，BC＝4，点O是AC的中点，以O为旋转中心，将△ABC绕点O旋转一周，A、B、C的对应点分别为A'、B'、C'，则BC'的最大值为　     　．

【答案】8

【完整解答】解：根据题意可知，点C’的运动路径为以O为圆心OC’长为半径的圆，

∴当B、O、C'共线且B、C'在O点异侧时BC'最大，

∴BC'的最大值为OB+OC'，

∵AC＝6，BC＝4，

∴OC=OC'=3，OB=5，

∴BC'的最大值为OB+OC'=5+3=8，

故答案为8.

【思路引导】根据题意可知，点C’的运动路径为以O为圆心OC’长为半径的圆，当B、O、C'共线且B、C'在O点异侧时BC'最大，然后根据勾股定理求出OB即可得.

17．（2分）（2021·南京一模）若点A与点B（1，1）关于点C（－1，－1）对称，则点A的坐标是　           　.

【答案】（-3，-3）

【完整解答】设点 的坐标为 ，

由题意得： ，解得 ，

则点 的坐标为（-3，-3），

故答案为：（-3，-3）.

【思路引导】根据中点坐标公式点（x1,y1）与（x2,y2）的中点坐标可得结果.

18．（2分）（2020九上·舒兰期末）如图，在平面直角坐标系中，抛物线y=x2+mx交x轴的负半轴于点A．点B是y轴正半轴上一点，点A关于点B的对称点A′恰好落在抛物线上．过点A′作x轴的平行线交抛物线于另一点C．若点A′的横坐标为1，则A′C的长为　     　．

【答案】3

【完整解答】当y=0时，x2+mx=0，解得x1=0，x2=﹣m，则A（﹣m，0），

∵点A关于点B的对称点为A′，点A′的横坐标为1，

∴点A的坐标为（﹣1，0），

∴抛物线解析式为y=x2+x，

当x=1时，y=x2+x=2，则A′（1，2），

当y=2时，x2+x=2，解得x1=﹣2，x2=1，则C（﹣2，1），

∴A′C的长为1﹣（﹣2）=3，

故答案为3．

【思路引导】点A关于点B的对称点为A′，点A′的横坐标为1，得出点A的坐标，得出抛物线解析式为y=x2+x，当x=1时、y=2时得出A'、C的坐标，即可得出A′C的长。

19．（2分）（2021九上·巧家期末）如图，正方形ABCD旋转后能与正方形CDEF重合，那么点A，B，C，D中，可以作为旋转中心的有　     　个.

【答案】2

【完整解答】把正方形ABCD绕点D逆时针旋转90°能与正方形CDEF重合，则旋转中心为点D；

把正方形ABCD绕点C顺时针旋转90°能与正方形CDEF重合，则旋转中心为点C；

综上，可以作为旋转中心的有2个.

故答案为：2.

【思路引导】利用旋转图形的性质，可得答案.

20．（2分）（2020九上·绥棱期末）如图，将n个边长都为1cm的正方形按如图所示摆放，点A1， A2，…，An分别是正方形的中心，则n个正方形重叠形成的重叠部分的面积和为 　     　

【答案】

【完整解答】解：由题意可得阴影部分面积等于正方形面积的 ，即是 ，

5个这样的正方形重叠部分（阴影部分）的面积和为 ×4，

n个这样的正方形重叠部分（阴影部分）的面积和为 ×（n-1）= cm2．

 【思路引导】根据题意可得出，阴影部分面积等于正方形面积的 ，已知两个正方形可得出一个阴影部分，则n个这样的正方形重叠部分为n-1阴影部分的和。

三．解答题（共7小题，满分60分）

21．（8分）（2022·平房模拟）如图，方格纸中每个小正方形的边长均为1个单位长度，的顶点、点D和线段EF的端点均在小正方形的顶点上．

（1）（4分）在方格纸中画出关于点D成中心对称的（点A的对称点是点M，点B的对称点是点N，点C的对称点是点P），点M、N、P在小正方形的顶点上；

（2）（4分）在方格纸中画出以EF为斜边的，且，点G在小正方形的顶点上．连接NG，请直接写出线段NG的长．

【答案】（1）解：如图，为所求作图形；

（2）解：如图，为所求作图形；

【完整解答】解：(1)，

在图上找到对应的点连线

【思路引导】（1）根据中心对称图形定义作出即可；
（2）先求出，再利用勾股定理求出NG的长即可。

22．（6分）（2021·包河模拟）如图，在平面直角坐标系中，已知 的三个顶点坐标分别是 ． 

⑴请画出 关于x轴对称的 ，并写出点 的坐标；

⑵以O为对称中心，画出 关于O成中心对称的图形 ；

⑶请用无刻度的直尺画出 的平分线 （点Q在线段 上）（保留作图辅助线）．

【答案】解：（1）如图所示， 即为所求，点 的坐标为 ； 

（2）如图所示；

（3）如图所示，在格点上分别取一点M、N，连接AN、CM，交于点J，作射线BJ，交AC于点Q，则BQ即为所求

【思路引导】（1）根据题意画出对称点连线即可；

（2）求出A、B、C关于原点的对称点的坐标连接即可；

（3）根据网格确定长度即可．

23．（4分）（2022八下·洋县期末）如图，在平面直角坐标系中，的三个顶点坐标分别为，，，的坐标为．（每个方格的边长均为1个单位长度）

⑴将平移，使点移动到点，请画出平移后的，点、的对应点分别是、；

⑵作出关于原点点成中心对称的，点、、的对应点分别是、、．

【答案】解：⑴如图，为所作．

⑵如图，为所作．
 

【思路引导】（1）把△ABC先向下平移2个单位，再向左平移4个单位，即可画出△A1B1C1；
（2）作出△ABC各顶点关于点O的对称点A2，B2，C2，再顺次连接，即可画出△A2B2C2.

24．（8分）（2022八下·晋中期末）下列三幅图中的网格均由边长为1的小正方形组成，图1是三国时期吴国的数学家赵爽所绘制的“弦图”，它由四个形状、大小完全相同的直角三角形组成，赵爽利用这“弦图”对勾股定理作出了证明，是中国古代数学的一项重要成就，请根据下列要求解答问题．

（1）（2分）图1中“弦图”的四个直角三角形组成的图形（阴影部分）是　     　（填“轴”或“中心”）对称图形；

（2）（6分）将“弦图”中的一个直角三角形作为基本图形，通过你所学过的图形变换知识，按下列要求画图：

①在图2中画出Rt△ABC向右平移4格后得到的△DEF；

②在图3中画出Rt△ABC绕点C顺时针旋转90°后得到的．

【答案】（1）中心

（2）解：如图所示

【完整解答】解：（1）解：“弦图”的四个直角三角形组成的图形（阴影部分）是中心对称图形；

故答案为：中心；

【思路引导】（1）利用中心对称图象的定义即可得解；
（2）①根据平移的性质将点A、B、C分别向右平移4格，可得对应点D、E、F，再顺次连接即可；
② 根据旋转的性质将点A、B、C分别确定绕点C顺时针旋转90°后的对应点A'、B'、C'，然后顺次连接即可；

25．（11分）（2022·蜀山模拟）如图，直角坐标系中的△ABC的三个顶点坐标分别为A（-5，0），B（-1，-4），C（-1，0），点M为线段AB的中点．

（1）（2分）点M关于y轴的对称点M的坐标为　          　；

（2）（4分）画出△ABC关于点O的中心对称图形△A1B1C1；（点A、B、C的对应点分别为点A1、B1、C1）；

（3）（5分）再将点M1沿y轴正方向平移，在平移过程中，直接写出当平移的距离d在什么范围时，点M1在A1B1C1的内部（不包括边界）．

【答案】（1）（3，-2）

（2）解：如图，

（3）解：直线A1B1的解析式为y=kx+b过（1，4）和（5，0）

∴

解得

∴y=-x+5

∴当x=3时，y=2

∴2＜d＜4

【完整解答】（1）解：（1）∵A（-5，0），B（-1，-4），

∴AB中点M的坐标为（-3，-2），

∴M关于y轴的对称点M′的坐标（3，-2），

故答案为：（3，-2）；

【思路引导】（1）根据关于y轴对称的点坐标的特征求解即可；
（2）根据中心对称的性质找出点A、B、C的对应点，再连接即可；
（3）先求出直线A1B1的解析式，再将x=3代入解析式求出y的值，即可得到d的取值范围。

26．（12分）（2022·东洲模拟）如图，抛物线经过A（），B（）两点，直线AB与轴交于点C．

（1）（4分）求抛物线的解析式；

（2）（4分）点M在抛物线上，点N在直线AB上，当M，N关于原点O成中心对称时，求点N的坐标；

（3）（4分）设P是抛物线对称轴上的一点，点Q在抛物线上，以A，B，P，Q为顶点的四边形能否成为平行四边形？若能，请直接写出点P的坐标；若不能，请说明理由．

【答案】（1）解：∵抛物线经过A（-1，0），B（）两点，

∴

解得

∴抛物线的解析式

（2）解：设直线AB的解析式为，

∵A（-1，0），B（）两点在直线AB上，

∴， 解得

∴.

设N（），则M（）

将M（）代入，得

，

解得，∴，

∴N的坐标为（，）或（，）

（3）解：能，

【完整解答】(3)解：设点Q（m，n），n=-m2+m+2，点P(1，s)，点A、B的坐标分别为(-1，0)、(4，-)，

①当AB是平行四边形的边时，

i)点B向右平移3个单位，点B在直线x=1上，

同样点A向右平移3个单位，此时横坐标为-4，

当x=-4时，y=-×(-4)2-4+=-10，

所以点A向上平移10个单位得到点Q，同样点B向上平移10个单位得到P，

∴s=-(10+)=-13，

∴点p坐标为(1，-13)；

ii) 点A向右平移2个单位，点A在直线x=1上，同样点B向右平移2个单位，此时横坐标为6，当x=6时，y=-×62+6+=-10，

所以点B向上平移-10-=8个单位得到点Q，同样点A向上平移8个单位得到P，则s=8，此时点P坐标为(1，-8)；

②当AB是平行四边形的对角线时，AB中点坐标为(，-)，

∴，∴m=2，

∴n=-×22+2+=，

∴，

解得：s=-4，

故点P（1，-4）

综上，故点P的坐标为：(1，-4)或(1，-8)或(1，-13)．

【思路引导】（1）将点A、B的坐标代入求出a、b的值即可；
（2）先求出直线AB的解析式为，设N（），则M（），将点M代入可得求出m的值，即可得到点N的坐标；
（3）分情况讨论，再利用平行四边形的性质列出方程求解即可。

27．（11分）（2021·东阳模拟）已知：如图， 的边 在x轴上， ，点B为 ，抛物线 经过点 ，点P为 的对称中心. 

（1）（5分）求此抛物线的函数表达式.

（2）（6分）平移抛物线，能否使平移后的抛物线同时经过点P，点C？若能，请写出平移方式，并说明理由.

【答案】（1）解：过点A作AD⊥x轴，如图所示：

∵四边形ABCO是平行四边形，

∴ ，

∵ ，

∴ ，

∴∠OAD=90°-∠AOC=30°，

∵点 ，

∴ ，

∴ ，

∴点 ，

把点A、B坐标代入抛物线 可得： ，

解得： ，

∴抛物线的解析式为 ；

（2）解：能使平移后的抛物线同时经过点P、C，平移方式为向左平移2个单位长度，再向下平移 个单位长度，理由如下： 

连接OB，如图所示：

由（1）可得抛物线的解析式为 ，则化为顶点式为 ，点 ，

∵点 ，

∴ ，

∴点 ，

∵点P为 的对称中心，

∴点P为 的中点，

∴根据中点坐标公式可得点 ，

设平移后的抛物线解析式为 ，把点P、C的坐标代入得：

，解得： ，

∴平移后的抛物线解析式为 ，化为顶点式为 ，

∴根据二次函数图象的平移可得：由抛物线 可先向左平移2个单位长度，再向下平移 个单位长度所得到.

【思路引导】（1） 过点A作AD⊥x轴，先求出∠OAD=30°，然后根据含30°角的直角三角形的性质求出点A的坐标，然后根据待定系数法求抛物线解析式即可；
（2）由于平行四边形是中心对称图形，根据中点坐标公式求出点P的坐标，设平移后的抛物线解析式为 ， 结合P、C点坐标，利用待定系数法求出平移后的解析式，将其化成顶点式，对比原解析式，即可得出平移的过程.