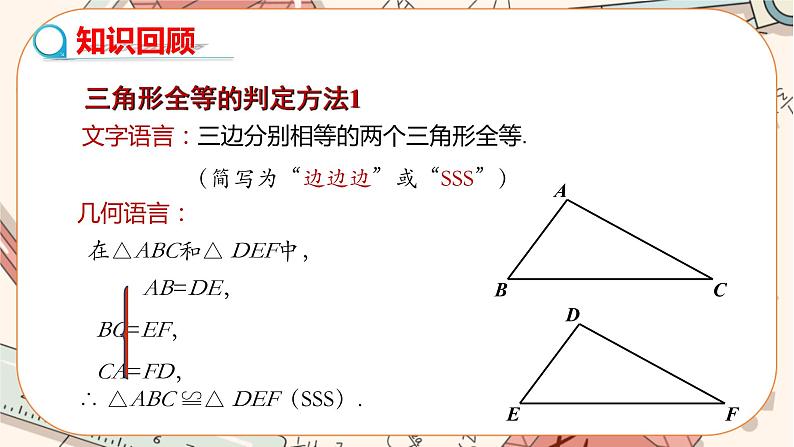
数学八年级上册12.1 全等三角形精品ppt课件

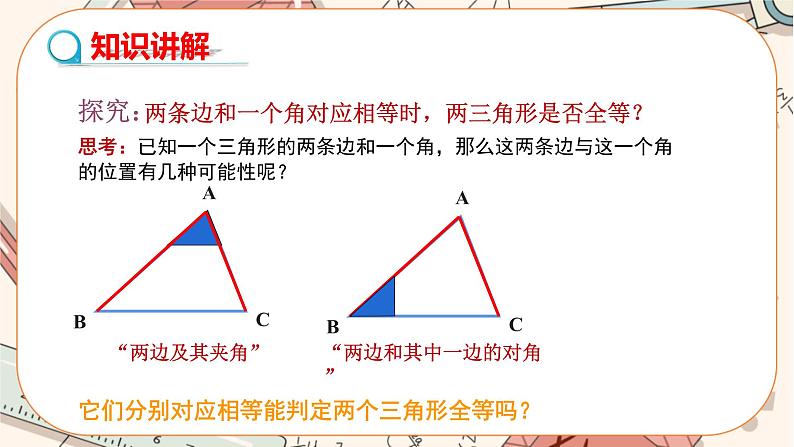
教学目标

1.掌握“边角边”定理的内容，能应用“边角边”判定两个三角形全等.

2.经历探索三角形全等的条件的过程，体会利用操作、归纳获得数学结论的方法.

3.培养学生观察分析图形的能力及运算能力，培养学生乐于探索的良好品质以及发现问题的能力.

教学重点难点

重点：应用“边角边”证明两个三角形全等，进而得出线段或角相等.

难点：指导学生分析问题，寻找判定三角形全等的条件.

教学过程

导入新课

导入一：

提出问题

（1）怎样的两个三角形是全等三角形？全等三角形的性质是什么？三角形全等的判定方法“SSS”的内容是什么？

（2）如果两个三角形有两条边和一个角分别对应相等，那么这两个三角形一定全等吗？此时应该有两种情况，一种是角夹在两条边的中间，形成两边一夹角，一种是角不夹在两边的中间，形成两边一对角，如图1所示.

图1

导入二：如图2所示，在湖泊的岸边有A，B两点，难以直接量出A，B两点间的距离.你能设计一种量出A，B两点之间距离的方案吗？说明你的设计理由.

图2

探究新知

活动一：

组织学生做游戏（找朋友），游戏规则：发放图3中的卡片若干张，利用全等三角形的概念找出与自己手中的三角形卡片全等的卡片所有者，即为朋友.

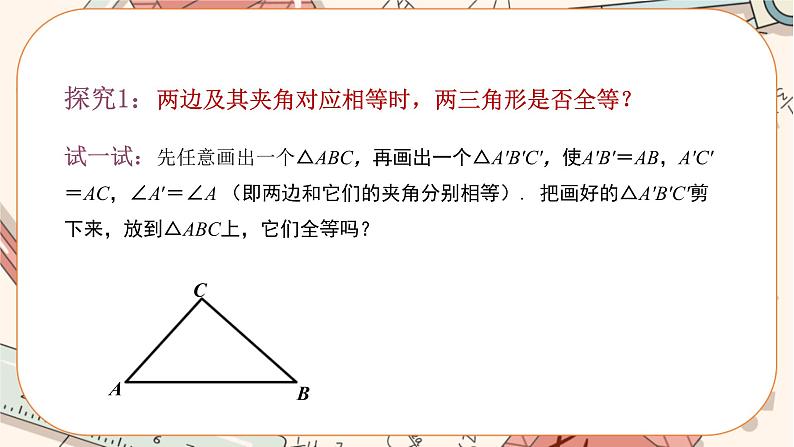
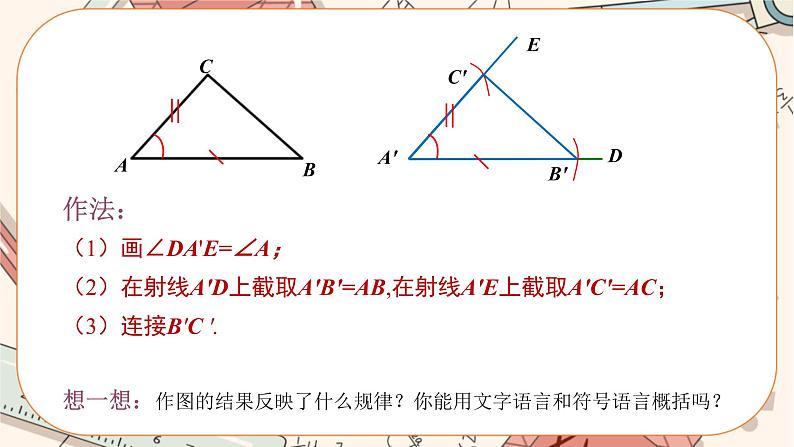
图3

教师：朋友的共同点是什么？

学生：两条边和它们的夹角对应相等.

活动二：

如图4①，已知△ABC，画△A′B′C′，使A′B′＝AB，A′C′＝AC，∠A′＝∠A.

画法：如图4②所示，（1）画∠DA′E＝∠A；

（2）在射线A′D上截取A′B′＝AB，在射线A′E上截取A′C′＝AC；

（3）连接B′C′.则△A′B′C′即为所求作的三角形.

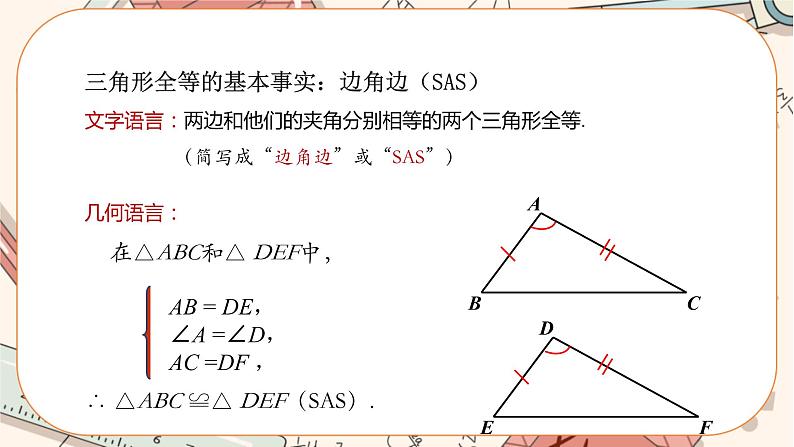
①　　　　　　　　　　　②　

图4

教师：把画好的△A′B′C′剪下来放在△ABC上，观察这两个三角形是否全等.为什么？

学生：全等，放在一起完全重合.

教师：这两个三角形全等是因为满足哪三个条件？

学生：两边一夹角分别相等.

根据前面的操作，鼓励学生用自己的语言来总结规律.

学生总结：两边和它们的夹角分别相等的两个三角形全等（可以简写成“边角边”或“SAS”）.

教师强调：角必须是已知两条边的夹角，边必须是已知角的两边.

几何语言：

在△ABC和△A′B′C′中，

∴ △ABC≌△A′B′C′（SAS）.

新知应用

例1　如图5，有一池塘，要测池塘两端A，B之间的距离，可先在平地上取一个可以直接到达A和B两点的点C，连接AC并延长到点D，使CD＝CA，连接BC并延长到点E，使CE＝CB，连接DE，那么量出DE的长就是A，B之间的距离，为什么？

图5

分析：如果能证明△ABC≌△DEC，就可以得出AB＝DE，由题意可知，△ABC和△DEC具备“边角边”的条件.

解：在△ABC和△DEC中，

∴ △ABC≌△DEC（SAS），

∴ AB＝DE.

归纳：因为全等三角形对应边相等，对应角相等，所以证明线段相等或角相等时，常常通过证明它们所在的两个三角形是全等三角形来解决.

活动三：教材第39页思考.

我们知道，两边和它们的夹角对应相等的两个三角形全等.由“两边及其中一边的对角对应相等”的条件能判定两个三角形全等吗？为什么？

如图6，把一长一短的两根细木棍的一端固定在一起，使长木棍的另一端与射线BC的端点B重合，固定住长木棍，把短木棍摆动，其另一端落在射线BC上的C点或D点，形成△OBC或△OBD，这个实验说明了什么？

图6

师生分析：图6中的△OBD和△OBC满足两边和其中一边的对角分别相等，即有OB＝OB，OC＝OD，∠B＝∠B，但

△OBD与△OBC不全等.

这说明：有两边和其中一边的对角分别相等的两个三角形不一定全等.

活动四：例题变式，深层思考

例2　已知：如图7，AB＝AC，AD＝AE，∠BAC＝∠DAE，求证：△ABD≌△ACE.

图7

证明：∵ ∠BAC＝∠DAE，

∴ ∠BAC+∠CAD＝∠DAE+∠CAD，

∴ ∠BAD＝∠CAE.

在△ABD和△ACE中，

∴ △ABD≌△ACE（SSS）.

课堂小结

1.三角形全等的判定：两边和它们的夹角分别相等的两个三角形全等（可以简写成“边角边”或“SAS”）.

2.求证两个三角形中的边或角相等时，一般要先证明这两个三角形全等.

注意：SAS中的角必须是两边的夹角，“A”必须在中间.

分层作业

必做：教材第39页练习第1，2题.

选做：1.在例2的条件中，请思考下列三个结论是否成立：

图8

（1）BD＝CE；（2）∠B＝∠C；

（3）∠ADB＝∠AEC.

2.如图8，AB⊥AC，AD⊥AE，AB＝AC，AD＝AE.

（1）求证：△DAC≌△EAB.

（2）请思考下列结论是否成立：

①BE＝DC，②∠B＝∠C，∠D＝∠E；

③BE⊥CD.

板书设计