



初中人教版12.1 全等三角形精品课件ppt
展开1. 三角形全等的性质是什么?
2. 如果两个三角形满足三条边对应相等,三个角对应相等,那么,这两个三角形全等吗?
3. 如果两个三角形满足上述六个条件中的一部分,是否也能保证两个三角形全等呢?
先任意画出一个△ABC,再画一个△A/B/C/,使△ABC与△A/B/C/满足上述六个条件中的一个或两个. 你画出的△A/B/C/与△ABC一定全等吗?
先任意画出一个△ABC,再画一个△A/B/C/,使A/B/=AB, B/C/ =BC,A/C/ =AC. 把画好的△A/B/C/剪下,放到△ABC上,它们全等吗?
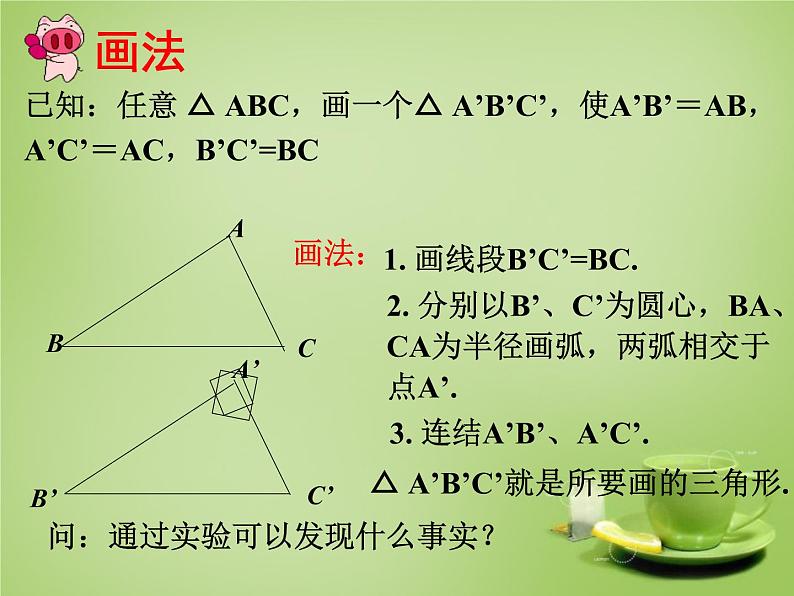
已知:任意 △ ABC,画一个△ A’B’C’,使A’B’=AB,A’C’=AC,B’C’=BC
1. 画线段B’C’=BC.
2. 分别以B’、C’为圆心,BA、CA为半径画弧,两弧相交于点A’.
3. 连结A’B’、A’C’.
△ A’B’C’就是所要画的三角形.
问:通过实验可以发现什么事实?
探究2反映的规律是: 三条边对应相等的两个三角形全等(简写成“边边边”或“SSS”)
三角形的三边长度固定,这个三角形的形状大小就完全确定,这个性质叫三角形的稳定性.
小结:用上面的结论可以判断两个三角形全等.判断两个三角形全等的推理过程,叫做证明三角形全等.
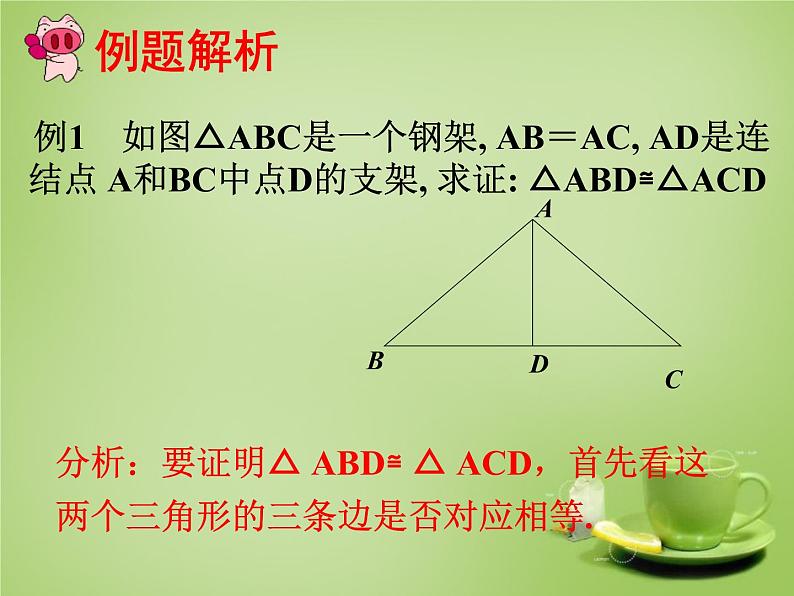
例1 如图△ABC是一个钢架, AB=AC, AD是连结点 A和BC中点D的支架, 求证: △ABD≌△ACD
分析:要证明△ ABD≌ △ ACD,首先看这两个三角形的三条边是否对应相等.
证明:∵D是BC的中点 ∴BD=CD 在△ABD和△ACD中,
AB=ACAD=ADDB=DC
∴ △ ABD≌ △ACD(SSS)
结论:从这题的证明中可以看出,证明是由题设(已知)出发,经过一步步的推理,最后推出结论正确的过程.
工人师傅常用角尺平分一个任意角.做法如下:已知∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合.过角尺顶点C的射线OC便是∠AOB的平分线.为什么?
已知:点A、E、F、C在同一条直线上, AD=CB,DF=BE,AE=CF.证明△ADF≌△CBE还应有什么条件?怎样才能得到这个条件?
如图,已知点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF. 求证:∠A=∠D.
证明:∵BE=CF(已知)
即 BC=EF
在△ABC和△DEF中
∴△ABC≌△DEF(SSS)
∴∠A=∠D(全等三角形对应角相等)
小结:欲证角相等,转化为证三角形全等.
∴ BE+EC=CF+EC
已知: 如图,AC=AD ,BC=BD. 求证: ∠C=∠D.
在△ACB 和 △ADB中
AC = A D BC = BD A B = A B (公共边)
(全等三角形对应角相等)
①∵E、F分别是AB,CD的中点( )
在△ADE与△CBF中
∴△ADE≌△CBF ( )
∴AE= AB CF= CD( )
3.如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,说出下列判断成立的理由.
∴ ∠A=∠C ( )
1. “SSS” ,三角形的稳定性及其应用.
2. 证角(或线段)相等转化为证角(或线段)所在的三角形全等;
初中第十二章 全等三角形12.1 全等三角形优质课课件ppt: 这是一份初中第十二章 全等三角形12.1 全等三角形优质课课件ppt
2020-2021学年12.1 全等三角形优秀ppt课件: 这是一份2020-2021学年12.1 全等三角形优秀ppt课件,文件包含121全等三角形课件pptx、121全等三角形教案doc、121全等三角形练习doc等3份课件配套教学资源,其中PPT共25页, 欢迎下载使用。
初中数学人教版八年级上册12.1 全等三角形教学ppt课件: 这是一份初中数学人教版八年级上册12.1 全等三角形教学ppt课件,共25页。













