资料中包含下列文件,点击文件名可预览资料内容





还剩6页未读,
继续阅读
所属成套资源:北师大版七年级数学下册同步练习
成套系列资料,整套一键下载
北师大版七年级数学下册——专题5.2探索轴对称的性质专项提升训练
展开
专题5.2探索轴对称的性质专项提升训练
班级:___________________ 姓名:_________________ 得分:_______________
注意事项:
本试卷满分120分,试题共24题,其中选择10道、填空6道、解答8道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2022秋•沭阳县校级月考)如图所示,图中的两个三角形沿AB折叠能完全重合,下列写法正确的是( )
A.△ABE≌△AFB B.△ABE≌△ABF C.△ABE≌△FBA D.△ABE≌△FAB
【分析】根据全等三角形的定义:能够完全重合的两个三角形叫做全等三角形求解即可.
【解答】解:∵图中的两个三角形沿AB折叠能完全重合,
∴△ABE≌△ABF,
故选:B.
2.(2022•哈尔滨模拟)如图,AD是△ABC的高,线段AE与线段AB关于AD对称,若∠B=35°,∠CAE=40°,则∠BAC的度数为( )
A.70° B.75° C.80° D.85°
【分析】先根据轴对称的性质得出∠B=∠E=35°,再根据三角形的内角和定理得出∠BAE=110°,最后根据∠BAC=∠BAE﹣∠CAE得出结论.
【解答】解:∵线段AE与线段AB关于AD对称,AD是△ABC的高,
∴∠B=∠E=35°,
∴∠BAE=180°﹣∠B﹣∠E=180°﹣35°﹣35°=110°,
∵∠CAE=40°,
∴∠BAC=∠BAE﹣∠CAE=110°﹣40°=70°,
故选:A.
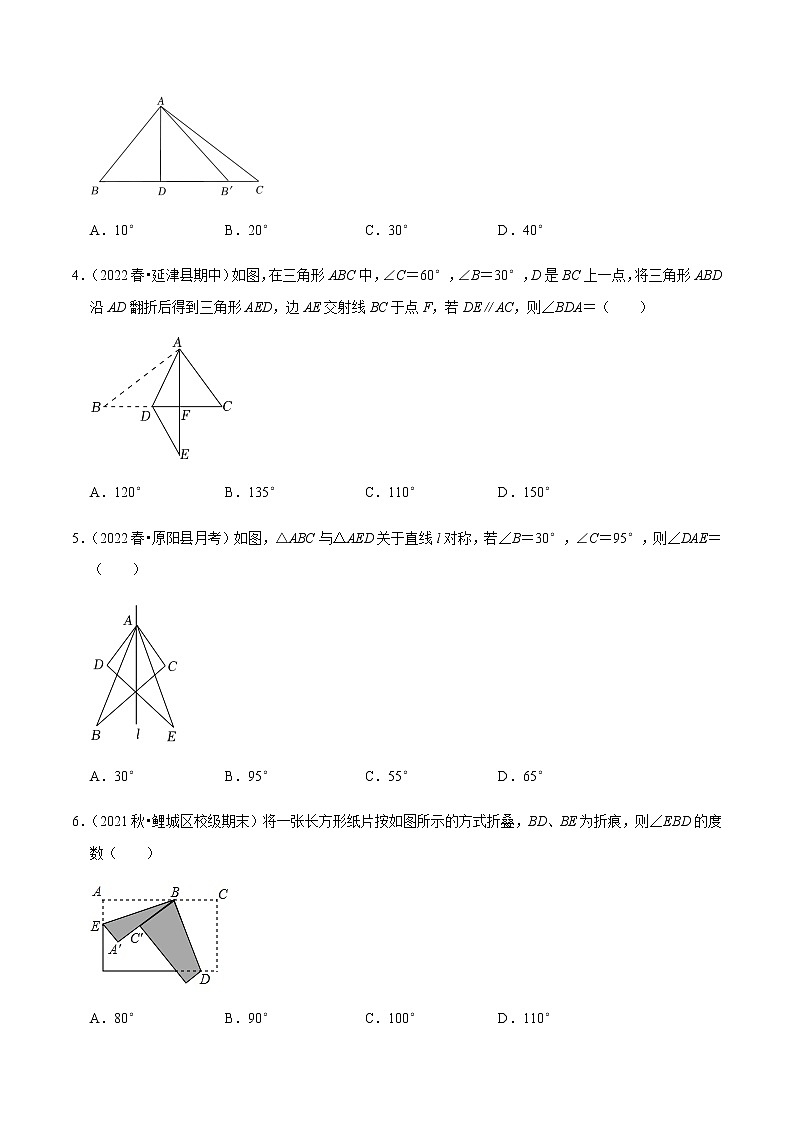
3.(2022春•隆回县期末)如图,在三角形ABC中,∠BAC=90°,AD⊥BC,垂足为D,∠BAD=40°,三角形ADB与三角形ADB′关于直线AD对称,点B的对称点是B′,则∠CAB′的度数为( )
A.10° B.20° C.30° D.40°
【分析】根据△ADB与△ADB'关于直线AD对称,点B的对称点是点B',得∠B'AD=∠BAD=40°,即得∠CAB'=∠BAC﹣∠B'AD﹣∠BAD=10°.
【解答】解:∵△ADB与△ADB'关于直线AD对称,点B的对称点是点B',
∴∠B'AD=∠BAD=40°,
∵∠BAC=90°,
∴∠CAB'=∠BAC﹣∠B'AD﹣∠BAD=90°﹣40°﹣40°=10°,
故选:A.
4.(2022春•延津县期中)如图,在三角形ABC中,∠C=60°,∠B=30°,D是BC上一点,将三角形ABD沿AD翻折后得到三角形AED,边AE交射线BC于点F,若DE∥AC,则∠BDA=( )
A.120° B.135° C.110° D.150°
【分析】由折叠性质可得∠E=∠B=30°,由平行线的性质可得∠E=∠CAE=30°,又三角形内角和定理可得∠BAC=90°,从而可得∠BAE=60°,即可得出∠BAD=30°,再利用三角形内角和定理可得∠BDA=120°.
【解答】解:∵∠C=60°,∠B=30°,
∵∠BAC=90°,
由折叠性质可得:
∠E=∠B=30°,∠BAD=∠EAD,
∵DE∥AC,
∴∠CAE=∠E=30°,
∴∠BAE=∠BAC﹣∠CAE=60°,
∴∠BAD=∠EAD=30°,
∴∠BDA=180°﹣∠B﹣∠BAD=120°,
故选:A.
5.(2022春•原阳县月考)如图,△ABC与△AED关于直线l对称,若∠B=30°,∠C=95°,则∠DAE=( )
A.30° B.95° C.55° D.65°
【分析】根据轴对称的性质以及三角形的内角和定理解决问题即可.
【解答】解:∵△ABC与△AED关于直线l对称,
∴△ABC≌△ED,
∴∠DAE=∠BAC,
∵∠BAC=180°﹣∠B﹣∠C=180°﹣30°﹣95°=55°,
∴∠DAE=55°.
故选:C.
6.(2021秋•鲤城区校级期末)将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕,则∠EBD的度数( )
A.80° B.90° C.100° D.110°
【分析】根据翻折的性质可知,∠ABE=∠A′BE,∠DBC=∠DBC′,又∵∠ABE+∠A′BE+∠DBC+∠DBC′=180°,且∠EBD=∠A′BE+∠DBC′,继而即可求出答案.
【解答】解:根据翻折的性质可知,∠ABE=∠A′BE,∠DBC=∠DBC′,
又∵∠ABE+∠A′BE+∠DBC+∠DBC′=180°,
∴∠EBD=∠A′BE+∠DBC′=180°×=90°.
故选:B.
7.(2021秋•宜兴市期末)将一张纸如图所示折叠后压平,点F在线段BC上,EF、GF为两条折痕,若∠EFG=α,则∠B'FC'的度数是( )
A.α﹣45° B.2α﹣90° C.90°﹣α D.180°﹣2α
【分析】由折叠的性质可知,∠EFB=∠EFB′,∠CFG=∠C′FG,推出∠EFB+∠CFG=180°﹣∠EFG=180°﹣α,∠EFB′+∠C′FG=180°﹣α,所以∠B'FC'=∠EFB+∠EFB′+∠CFG+∠C′FG﹣180°=(180°﹣α)+(180°﹣α)﹣180°=180°﹣2α.
【解答】解:由折叠的性质可知,∠EFB=∠EFB′,∠CFG=∠C′FG,
∵∠EFG=α,
∴∠EFB+∠CFG=180°﹣∠EFG=180°﹣α,
∴∠EFB′+∠C′FG=180°﹣α,
∴∠B'FC'=∠EFB+∠EFB′+∠CFG+∠C′FG﹣180°
=(180°﹣α)+(180°﹣α)﹣180°
=180°﹣2α,
故选:D.
8.(2021秋•卢龙县校级期末)如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处.若∠B=70°,则∠BDF等于( )
A.65° B.50° C.40° D.37.5°
【分析】先根据图形翻折不变性的性质可得AD=DF,根据等边对等角的性质可得∠B=∠BFD,再根据三角形的内角和定理列式计算即可求解.
【解答】解:∵△DEF是△DEA沿直线DE翻折变换而来,
∴AD=DF,
∵D是AB边的中点,
∴AD=BD,
∴BD=DF,
∴∠B=∠BFD,
∵∠B=70°,
∴∠BDF=180°﹣∠B﹣∠BFD=180°﹣70°﹣70°=40°.
故选:C.
9.(2022秋•临洮县期中)如图,在△ABC中,∠A=20°,∠B=60°,将点A与点B分别沿MN和EF折叠,使点A、B与点C重合,则∠NCF的度数为( )
A.22° B.21° C.20° D.19°
【分析】先根据三角形内角和定理求出∠ACB的度数,再由图形翻折变换的性质得出∠MCN与∠ECF的度数,进而可得出结论.
【解答】解:在△ABC中,
∵∠A=20°,∠B=60°,
∴∠ACB=180°﹣∠A﹣∠B=180°﹣20°﹣60°=100°.
∵点A与点B分别沿MN和EF折叠,使点A、B与点C重合,
∴∠MCN=∠A=20°,∠ECF=∠B=60°,
∴∠NCF=∠ACB﹣∠MCN﹣∠ECF=100°﹣20°﹣60°=20°.
故选:C.
10.(2022秋•新华区校级期中)如图,∠AOB=30°,点P是∠AOB内的一个定点,OP=12cm,点C、D分别是OA、OB上的动点,连接CP、DP、CD,则△CPD周长的最小值为( )
A.10cm B.12cm C.15cm D.24cm
【分析】作点P关于OA、OB的对称点P′、P″,连接P′P″分别与OA、OB相交,根据轴对称确定最短路线问题,交点即为所求点C、D,△CPD周长的最小值等于P′P″,根据轴对称的性质可得∠POA=∠P′OA,∠POB=∠P″OB,OP′=OP″=OP,然后求出∠P′OP″=60°,从而判断出△OP′P″是等边三角形,根据等边三角形的性质可得PP′=OP′.
【解答】解:如图,作点P关于OA、OB的对称点P′、P″,连接P′P″,
由轴对称确定最短路线问题,P′P″分别与OA、OB的交点即为C、D,
△CPD周长的最小值=P′P″,
由轴对称的性质,∠POA=∠P′OA,∠POB=∠P″OB,OP′=OP″=OP=12cm,
所以,∠P′OP″=2∠AOB=2×30°=60°,
所以,△OP′P″是等边三角形,
∴PP′=OP′=12cm.
故选:B.
二、填空题(本大题共6小题,每小题3分,共18分)请把答案直接填写在横线上
11.(2021秋•宝山区期末)如图,在△ABC中,AB=9,BC=7,CA=5,将△ABC沿直线l折叠,恰好使点B与点A重合,直线l交边BC于点D,那么△ACD的周长是 12 .
【分析】由翻折可得BD=AD,故△ACD的周长是AC+BC,即可求得答案.
【解答】解:∵将△ABC沿直线l折叠,恰好使点B与点A重合,
∴BD=AD,
∴BC=BD+CD=AD+CD,
∵△ACD的周长是AC+AD+CD,
∴△ACD的周长是AC+BC=5+7=12,
故答案为:12.
12.(2022秋•广饶县校级月考)如图,将一张长方形纸片ABCD沿EF折叠,点D、C分别落在D'、C'的位置处,若∠1=50°,则∠DEF的度数是 65 °.
【分析】根据平角的定义可得∠DED′=130°,再根据折叠的性质可得∠D′EF=∠DEF=65°.
【解答】解:∵∠1=50°,
∴∠DED′=130°,
∵四边形DEFC折叠得到四边形D′EFC′,
∴∠D′EF=∠DEF=65°.
故答案为:65.
13.(2022秋•鼓楼区校级月考)如图,△ABC中,∠B=60°,∠C=56°,点D为BC边上一动点.分别作点D关于AB,AC的对称点E,F,连接AE,AF.则∠EAF的度数等于 128 °.
【分析】由点E和点F分别是点D关于AB和AC的对称点,得∠EAB=∠BAD,∠FAC=∠CAD,再根据∠B=60°,∠C=56°,所以∠BAC=∠BAD+∠DAC=180°﹣60°﹣56°=64°,即可求出答案.
【解答】解:如图,连接AD,DE,DF,
∵点E和点F分别是点D关于AB和AC的对称点,
∴∠EAB=∠BAD,∠FAC=∠CAD,
∵∠B=60°,∠C=56°,
∴∠BAC=∠BAD+∠DAC=180°﹣60°﹣56°=64°,
∴∠EAF=2∠BAC=128°,
故答案为:128.
14.(2022秋•丰满区期末)如图,在△ABC中,DE∥AC,∠C=51°,∠B=29°,将△ABC沿DE折叠,点B的对应点是点B',则∠BEB'的度数是 160° .
【分析】根据三角形的内角和定理,平行线的性质以及周角的定义即可得到结论.
【解答】解:∵∠C=51°,∠B=29°,
∴∠A=180°﹣51°﹣29°=100°,
∵DE∥AC,
∴∠BED=∠A=100°,
由折叠的性质可知,∠DEB′=∠BED=100°,
∴∠BEB′=360°﹣100°﹣100°=160°,
故答案为:160°.
15.(2022秋•密山市校级期末)如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=20,则△PMN的周长为 20 .
【分析】根据轴对称的性质可得PM=P1M,PN=P2N,然后求出△PMN的周长=P1P2.
【解答】解:∵点P关于OA、OB的对称点P1、P2,
∴PM=P1M,PN=P2N,
∴△PMN的周长=PM+MN+PN=P1M+MN+P2N=P1P2,
∵P1P2=20,
∴△PMN的周长=20.
故答案为:20.
16.(2022秋•桂平市期中)如图,∠AOB=30°,点P为∠AOB内一点,OP=10.点M、N分别在OA、OB上.当△PMN周长最小时,下列结论:
①∠MPN等于120°;
②∠MPN等于110°;
③∠MPN等于100°;
④△PMN周长最小值是5:
⑤△PMN周长最小值是10;
⑥△PMN周长最小值是15.
其中正确结论的序号是 ①⑤ .
【分析】分别作点P关于OA、OB的对称点P1、P2,连P1、P2,交OA于M,交OB于N,△PMN的周长=P1P2,然后证明△OP1P2是等边三角形,即可求解.
【解答】解:分别作点P关于OA、OB的对称点P1、P2,连PP1、PP2,交OA于M,交OB于N,
则OP1=OP=OP2,∠P1OA=∠POA,∠POB=∠P2OB,MP=P1M,PN=P2N,
则△PMN的周长的最小值=P1P2
∴∠P1OP2=2∠AOB=60°,
∴△OP1P2是等边三角形,
∴∠MPN=∠OPM+∠OPN=∠OP1M+∠OP2N=120°,
∵△PMN的周长=P1P2,P1P2=OP1=OP2=OP=10,
∴△PMN的周长=10.
∴①⑤正确,
故答案为①⑤.
三、解答题(本大题共8小题,共72分.解答时应写出文字说明、证明过程或演算步骤)
17.(2021秋•涟水县校级月考)如图,△ABC与△DEF关于直线MN对称,其中∠C=90°,AC=8cm,DE=10cm,BC=6cm.
(1)线段AD与MN的关系是什么?
(2)求∠F的度数;
(3)求△ABC的周长和△DEF的面积.
【分析】(1)利用关于某条直线对称的两个图形的对称点的连线被对称轴垂直平分可以得到;
(2)利用关于某条直线对称的三角形全等可以得到对应角相等;
(3)利用关于某条直线对称的三角形全等可以得到周长和面积相等;
【解答】解:(1)∵△ABC与△DEF关于直线MN对称,
∴MN垂直平分AD;
(2)∵△ABC与△DEF关于直线MN对称,
∴△ABC≌△DEF,
∵∠C=∠F=90°;
(3)∵AC=8cm,DE=10cm,BC=6cm,
∴DE=AB=10cm,
∴△ABC的周长=6+8+10=24cm;
△DEF的面积=×6×8=24cm2.
18.(2021秋•剑川县校级期中)如图,在Rt△ABC中,∠ACB=90゜,∠A=50゜,将其折叠,使点A落在边CB上A′处,折痕为CD.求∠A′DB的度数.
【分析】根据折叠性质得出∠DCA=∠BCD=45°,∠CDA=∠CDA′,求出∠CDA、∠CDA′,根据三角形外角性质求出∠BDC,即可求出答案.
【解答】解:∵将△ACD折叠,使点A落在边CB上A′处,折痕为CD,∠ACB=90°,
∴∠DCA=∠BCD=45°,∠CDA=∠CDA′,
∴∠CDA=180°﹣∠DCA﹣∠A=180°﹣45°﹣50°=85°,
∴∠CDA′=85°,
∵∠BDC=∠A+∠DCA=50°+45°=95°,
∴∠A′DB=∠BDC﹣∠A′DC=95°﹣85°=10°.
19.(2020秋•东台市月考)直线MN和同侧两点AB,在MN上找一点P,使得PA+PB最小.(尺规作图)
【分析】作点B关于MN的对称点B′,则有PB=PB′,根据两点之间线段最短可得,当A、P、B′三点共线时,PA+PB=PA+PB′最短,故AB′与MN的交点即为所求点P.
【解答】解:以点B为圆心,某一长度为半径画弧,交MN于C、D两点,
以点C为圆心,BC为半径画圆,再以点D为圆心,DB为半径画圆,
设两圆的另一个交点为B′,连接AB′,交MN于P,连接PB,如图所示,
点P即为所求作.
20.(2020春•吉安期中)如图,小丽将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,试求△ACD的周长.
(2)如果∠CAD:∠BAD=4:7,求∠B的度数.
【分析】(1)根据轴对称的性质就可以得出BD=AD,就有△ACD的周长AD+AC+CD=BD+CD+AC而求出结论;
(2)设每份为x°,则∠CAD=4x,∠BAD=7x,由BD=AD可以求出∠B=∠BAD=7x,由直角三角形的性质就可以求出结论.
【解答】解:∵△BDE与△ADE成轴对称,
∴BD=AD,∠B=∠BAD.
∵△ACD的周长=AC+AD+CD,
∴△ACD的周长=AC+BD+CD=AC+BC.
∵AC=6cm,BC=8cm,
∴△ACD的周长=6+8=14cm;
(2)设每份为x°,则∠CAD=4x,∠BAD=7x,
∵∠B=∠BAD,
∴∠B=7x,
∵∠B+∠DAB+∠CAD=90°,
∴7x+7x+4x=90,
∴x=5,
∴∠B=35°.
答:∠B的度数是35°.
21.(2018秋•澧县期末)如图,点A、B在直线l的同侧,点B′是B点关于l的对称点,AB′交l于点P.
(1)AB′与AP+PB相等吗?为什么?
(2)在l上再取一点Q,并连接AQ和QB,比较AQ+QB与AP+PB的大小,并说明理由.
【分析】(1)由轴对称的性质,对称点的连线被对称轴垂直平分,可得PB=PB′,即可得证AB′=AP+PB;
(2)连接QB′,由轴对称的性质可得:QB=QB′,然后根据两点之间线段最短(三角形的三边关系)可得:AQ+QB′>AB′,即AQ+QB>AP+PB.
【解答】解:(1)AB′与AP+PB相等,连接BB′,
∵点B′是B点关于l的对称点,
∴l垂直平分线段BB′,
∴PB=PB′,
∴AP+PB′=AP+BP,
即:AB′=AP+BP;
(2)AQ+QB>AP+PB,
连接QB′,如图所示,
∵点B′是B点关于l的对称点,
∴l垂直平分线段BB′,
∴BQ=QB′,
∵AQ+QB′>AB′,
∴AQ+BQ>AB′,
∵AB′=AP+BP,
∴AQ+QB>AP+PB.
22.(2019秋•横县期中)如图所示,已知Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形,使C点落在AB边上的点D、要使点D恰为AB的中点,问在图中还要添加什么条件?(直接填写答案)
(1)写出两条边满足的条件: BC=AB ;
(2)写出两个角满足的条件: ∠ABC=2∠A ;
(3)写出一个除边、角以外的其他满足条件: △BEC≌△AED .
【分析】(1)根据题意可得要使D在中点,则一定有BC=AB,围绕此条件可推出两边满足的条件.
(2)由轴对称的性质可得出两角满足的条件.
(3)可以写全等的条件.
【解答】解:(1)①AB=BC
证明:由轴对称的性质可得:BC=BD,又因为BC=AB=BD
∴可得D在AB的中点位置.
(2)①∠ABC=2∠A.
∵∠C=90°,
∴∠ABC+∠A=90°.
∵∠ABC=2∠A,
∴∠A=30°.
由轴对称的性质得:BC=BD,CE=DE,∠CBE=∠DBE=∠A=30°.
∴△ADE≌△BCE,AD=BC=BD.
即点D在AB的中点;
(3)△BEC≌△AED
证明:∵△BEC≌△AED
∴可得:AD=DB
故证得点D在AB的中点.
23.(2021秋•大同区校级期末)如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q落在线段MN上,点P关于OB的对称点R落在MN的延长线上,若,MN=a,QR=b,其中a<b,试求PN﹣PM的值.(用a和b表示)
【分析】由轴对称的性质可得RN=PN,MQ=MP,于是推出PN﹣PM=QR﹣MN,即可得到答案.
【解答】解:∵点P关于OA的对称点Q落在线段MN上,点P关于OB的对称点R落在MN上,
∴RN=PN,MQ=MP,
∴PN﹣PM=RN﹣MQ,
∴PN﹣PM=(RN+NQ)﹣(MQ+NQ)=QR﹣MN=b﹣a.
24.(2022秋•威县校级月考)如图,在△ABC中,∠CAB=36°,∠B=48°,D,E分别是边AB和BC上的点,△ACE和△ADE关于直线AE对称,CD交AE于点F.
(1)求∠ADC的度数;
(2)求∠DEB的度数.
【分析】(1)直接利用轴对称的性质得出AC=AD,再利用等腰三角形的性质以及三角形内角和定理得出答案;
(2)直接利用轴对称的性质得出EC=ED,再利用等腰三角形的性质以及三角形外角的性质得出答案.
【解答】解:(1)∵△ACE和△ADE关于直线AE对称,
∴AC=AD,
∴∠ACD=∠ADC,
∵∠CAB=36°,
∴∠ADC=∠ACD==72°;
(2)∵△ACE和△ADE关于直线AE对称,
∴EC=DE,
∴∠ECD=∠EDC,
∵∠CAB=36°,∠B=48°,∠ACD=72°,
∴∠DCB=180°﹣36°﹣48°﹣72°=24°,
∴∠ECD=∠EDC=24°,
∴∠DEB=48°.
班级:___________________ 姓名:_________________ 得分:_______________
注意事项:
本试卷满分120分,试题共24题,其中选择10道、填空6道、解答8道.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置.
一、选择题(本大题共10小题,每小题3分,共30分)在每小题所给出的四个选项中,只有一项是符合题目要求的.
1.(2022秋•沭阳县校级月考)如图所示,图中的两个三角形沿AB折叠能完全重合,下列写法正确的是( )
A.△ABE≌△AFB B.△ABE≌△ABF C.△ABE≌△FBA D.△ABE≌△FAB
【分析】根据全等三角形的定义:能够完全重合的两个三角形叫做全等三角形求解即可.
【解答】解:∵图中的两个三角形沿AB折叠能完全重合,
∴△ABE≌△ABF,
故选:B.
2.(2022•哈尔滨模拟)如图,AD是△ABC的高,线段AE与线段AB关于AD对称,若∠B=35°,∠CAE=40°,则∠BAC的度数为( )
A.70° B.75° C.80° D.85°
【分析】先根据轴对称的性质得出∠B=∠E=35°,再根据三角形的内角和定理得出∠BAE=110°,最后根据∠BAC=∠BAE﹣∠CAE得出结论.
【解答】解:∵线段AE与线段AB关于AD对称,AD是△ABC的高,
∴∠B=∠E=35°,
∴∠BAE=180°﹣∠B﹣∠E=180°﹣35°﹣35°=110°,
∵∠CAE=40°,
∴∠BAC=∠BAE﹣∠CAE=110°﹣40°=70°,
故选:A.
3.(2022春•隆回县期末)如图,在三角形ABC中,∠BAC=90°,AD⊥BC,垂足为D,∠BAD=40°,三角形ADB与三角形ADB′关于直线AD对称,点B的对称点是B′,则∠CAB′的度数为( )
A.10° B.20° C.30° D.40°
【分析】根据△ADB与△ADB'关于直线AD对称,点B的对称点是点B',得∠B'AD=∠BAD=40°,即得∠CAB'=∠BAC﹣∠B'AD﹣∠BAD=10°.
【解答】解:∵△ADB与△ADB'关于直线AD对称,点B的对称点是点B',
∴∠B'AD=∠BAD=40°,
∵∠BAC=90°,
∴∠CAB'=∠BAC﹣∠B'AD﹣∠BAD=90°﹣40°﹣40°=10°,
故选:A.
4.(2022春•延津县期中)如图,在三角形ABC中,∠C=60°,∠B=30°,D是BC上一点,将三角形ABD沿AD翻折后得到三角形AED,边AE交射线BC于点F,若DE∥AC,则∠BDA=( )
A.120° B.135° C.110° D.150°
【分析】由折叠性质可得∠E=∠B=30°,由平行线的性质可得∠E=∠CAE=30°,又三角形内角和定理可得∠BAC=90°,从而可得∠BAE=60°,即可得出∠BAD=30°,再利用三角形内角和定理可得∠BDA=120°.
【解答】解:∵∠C=60°,∠B=30°,
∵∠BAC=90°,
由折叠性质可得:
∠E=∠B=30°,∠BAD=∠EAD,
∵DE∥AC,
∴∠CAE=∠E=30°,
∴∠BAE=∠BAC﹣∠CAE=60°,
∴∠BAD=∠EAD=30°,
∴∠BDA=180°﹣∠B﹣∠BAD=120°,
故选:A.
5.(2022春•原阳县月考)如图,△ABC与△AED关于直线l对称,若∠B=30°,∠C=95°,则∠DAE=( )
A.30° B.95° C.55° D.65°
【分析】根据轴对称的性质以及三角形的内角和定理解决问题即可.
【解答】解:∵△ABC与△AED关于直线l对称,
∴△ABC≌△ED,
∴∠DAE=∠BAC,
∵∠BAC=180°﹣∠B﹣∠C=180°﹣30°﹣95°=55°,
∴∠DAE=55°.
故选:C.
6.(2021秋•鲤城区校级期末)将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕,则∠EBD的度数( )
A.80° B.90° C.100° D.110°
【分析】根据翻折的性质可知,∠ABE=∠A′BE,∠DBC=∠DBC′,又∵∠ABE+∠A′BE+∠DBC+∠DBC′=180°,且∠EBD=∠A′BE+∠DBC′,继而即可求出答案.
【解答】解:根据翻折的性质可知,∠ABE=∠A′BE,∠DBC=∠DBC′,
又∵∠ABE+∠A′BE+∠DBC+∠DBC′=180°,
∴∠EBD=∠A′BE+∠DBC′=180°×=90°.
故选:B.
7.(2021秋•宜兴市期末)将一张纸如图所示折叠后压平,点F在线段BC上,EF、GF为两条折痕,若∠EFG=α,则∠B'FC'的度数是( )
A.α﹣45° B.2α﹣90° C.90°﹣α D.180°﹣2α
【分析】由折叠的性质可知,∠EFB=∠EFB′,∠CFG=∠C′FG,推出∠EFB+∠CFG=180°﹣∠EFG=180°﹣α,∠EFB′+∠C′FG=180°﹣α,所以∠B'FC'=∠EFB+∠EFB′+∠CFG+∠C′FG﹣180°=(180°﹣α)+(180°﹣α)﹣180°=180°﹣2α.
【解答】解:由折叠的性质可知,∠EFB=∠EFB′,∠CFG=∠C′FG,
∵∠EFG=α,
∴∠EFB+∠CFG=180°﹣∠EFG=180°﹣α,
∴∠EFB′+∠C′FG=180°﹣α,
∴∠B'FC'=∠EFB+∠EFB′+∠CFG+∠C′FG﹣180°
=(180°﹣α)+(180°﹣α)﹣180°
=180°﹣2α,
故选:D.
8.(2021秋•卢龙县校级期末)如图,已知D为△ABC边AB的中点,E在AC上,将△ABC沿着DE折叠,使A点落在BC上的F处.若∠B=70°,则∠BDF等于( )
A.65° B.50° C.40° D.37.5°
【分析】先根据图形翻折不变性的性质可得AD=DF,根据等边对等角的性质可得∠B=∠BFD,再根据三角形的内角和定理列式计算即可求解.
【解答】解:∵△DEF是△DEA沿直线DE翻折变换而来,
∴AD=DF,
∵D是AB边的中点,
∴AD=BD,
∴BD=DF,
∴∠B=∠BFD,
∵∠B=70°,
∴∠BDF=180°﹣∠B﹣∠BFD=180°﹣70°﹣70°=40°.
故选:C.
9.(2022秋•临洮县期中)如图,在△ABC中,∠A=20°,∠B=60°,将点A与点B分别沿MN和EF折叠,使点A、B与点C重合,则∠NCF的度数为( )
A.22° B.21° C.20° D.19°
【分析】先根据三角形内角和定理求出∠ACB的度数,再由图形翻折变换的性质得出∠MCN与∠ECF的度数,进而可得出结论.
【解答】解:在△ABC中,
∵∠A=20°,∠B=60°,
∴∠ACB=180°﹣∠A﹣∠B=180°﹣20°﹣60°=100°.
∵点A与点B分别沿MN和EF折叠,使点A、B与点C重合,
∴∠MCN=∠A=20°,∠ECF=∠B=60°,
∴∠NCF=∠ACB﹣∠MCN﹣∠ECF=100°﹣20°﹣60°=20°.
故选:C.
10.(2022秋•新华区校级期中)如图,∠AOB=30°,点P是∠AOB内的一个定点,OP=12cm,点C、D分别是OA、OB上的动点,连接CP、DP、CD,则△CPD周长的最小值为( )
A.10cm B.12cm C.15cm D.24cm
【分析】作点P关于OA、OB的对称点P′、P″,连接P′P″分别与OA、OB相交,根据轴对称确定最短路线问题,交点即为所求点C、D,△CPD周长的最小值等于P′P″,根据轴对称的性质可得∠POA=∠P′OA,∠POB=∠P″OB,OP′=OP″=OP,然后求出∠P′OP″=60°,从而判断出△OP′P″是等边三角形,根据等边三角形的性质可得PP′=OP′.
【解答】解:如图,作点P关于OA、OB的对称点P′、P″,连接P′P″,
由轴对称确定最短路线问题,P′P″分别与OA、OB的交点即为C、D,
△CPD周长的最小值=P′P″,
由轴对称的性质,∠POA=∠P′OA,∠POB=∠P″OB,OP′=OP″=OP=12cm,
所以,∠P′OP″=2∠AOB=2×30°=60°,
所以,△OP′P″是等边三角形,
∴PP′=OP′=12cm.
故选:B.
二、填空题(本大题共6小题,每小题3分,共18分)请把答案直接填写在横线上
11.(2021秋•宝山区期末)如图,在△ABC中,AB=9,BC=7,CA=5,将△ABC沿直线l折叠,恰好使点B与点A重合,直线l交边BC于点D,那么△ACD的周长是 12 .
【分析】由翻折可得BD=AD,故△ACD的周长是AC+BC,即可求得答案.
【解答】解:∵将△ABC沿直线l折叠,恰好使点B与点A重合,
∴BD=AD,
∴BC=BD+CD=AD+CD,
∵△ACD的周长是AC+AD+CD,
∴△ACD的周长是AC+BC=5+7=12,
故答案为:12.
12.(2022秋•广饶县校级月考)如图,将一张长方形纸片ABCD沿EF折叠,点D、C分别落在D'、C'的位置处,若∠1=50°,则∠DEF的度数是 65 °.
【分析】根据平角的定义可得∠DED′=130°,再根据折叠的性质可得∠D′EF=∠DEF=65°.
【解答】解:∵∠1=50°,
∴∠DED′=130°,
∵四边形DEFC折叠得到四边形D′EFC′,
∴∠D′EF=∠DEF=65°.
故答案为:65.
13.(2022秋•鼓楼区校级月考)如图,△ABC中,∠B=60°,∠C=56°,点D为BC边上一动点.分别作点D关于AB,AC的对称点E,F,连接AE,AF.则∠EAF的度数等于 128 °.
【分析】由点E和点F分别是点D关于AB和AC的对称点,得∠EAB=∠BAD,∠FAC=∠CAD,再根据∠B=60°,∠C=56°,所以∠BAC=∠BAD+∠DAC=180°﹣60°﹣56°=64°,即可求出答案.
【解答】解:如图,连接AD,DE,DF,
∵点E和点F分别是点D关于AB和AC的对称点,
∴∠EAB=∠BAD,∠FAC=∠CAD,
∵∠B=60°,∠C=56°,
∴∠BAC=∠BAD+∠DAC=180°﹣60°﹣56°=64°,
∴∠EAF=2∠BAC=128°,
故答案为:128.
14.(2022秋•丰满区期末)如图,在△ABC中,DE∥AC,∠C=51°,∠B=29°,将△ABC沿DE折叠,点B的对应点是点B',则∠BEB'的度数是 160° .
【分析】根据三角形的内角和定理,平行线的性质以及周角的定义即可得到结论.
【解答】解:∵∠C=51°,∠B=29°,
∴∠A=180°﹣51°﹣29°=100°,
∵DE∥AC,
∴∠BED=∠A=100°,
由折叠的性质可知,∠DEB′=∠BED=100°,
∴∠BEB′=360°﹣100°﹣100°=160°,
故答案为:160°.
15.(2022秋•密山市校级期末)如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=20,则△PMN的周长为 20 .
【分析】根据轴对称的性质可得PM=P1M,PN=P2N,然后求出△PMN的周长=P1P2.
【解答】解:∵点P关于OA、OB的对称点P1、P2,
∴PM=P1M,PN=P2N,
∴△PMN的周长=PM+MN+PN=P1M+MN+P2N=P1P2,
∵P1P2=20,
∴△PMN的周长=20.
故答案为:20.
16.(2022秋•桂平市期中)如图,∠AOB=30°,点P为∠AOB内一点,OP=10.点M、N分别在OA、OB上.当△PMN周长最小时,下列结论:
①∠MPN等于120°;
②∠MPN等于110°;
③∠MPN等于100°;
④△PMN周长最小值是5:
⑤△PMN周长最小值是10;
⑥△PMN周长最小值是15.
其中正确结论的序号是 ①⑤ .
【分析】分别作点P关于OA、OB的对称点P1、P2,连P1、P2,交OA于M,交OB于N,△PMN的周长=P1P2,然后证明△OP1P2是等边三角形,即可求解.
【解答】解:分别作点P关于OA、OB的对称点P1、P2,连PP1、PP2,交OA于M,交OB于N,
则OP1=OP=OP2,∠P1OA=∠POA,∠POB=∠P2OB,MP=P1M,PN=P2N,
则△PMN的周长的最小值=P1P2
∴∠P1OP2=2∠AOB=60°,
∴△OP1P2是等边三角形,
∴∠MPN=∠OPM+∠OPN=∠OP1M+∠OP2N=120°,
∵△PMN的周长=P1P2,P1P2=OP1=OP2=OP=10,
∴△PMN的周长=10.
∴①⑤正确,
故答案为①⑤.
三、解答题(本大题共8小题,共72分.解答时应写出文字说明、证明过程或演算步骤)
17.(2021秋•涟水县校级月考)如图,△ABC与△DEF关于直线MN对称,其中∠C=90°,AC=8cm,DE=10cm,BC=6cm.
(1)线段AD与MN的关系是什么?
(2)求∠F的度数;
(3)求△ABC的周长和△DEF的面积.
【分析】(1)利用关于某条直线对称的两个图形的对称点的连线被对称轴垂直平分可以得到;
(2)利用关于某条直线对称的三角形全等可以得到对应角相等;
(3)利用关于某条直线对称的三角形全等可以得到周长和面积相等;
【解答】解:(1)∵△ABC与△DEF关于直线MN对称,
∴MN垂直平分AD;
(2)∵△ABC与△DEF关于直线MN对称,
∴△ABC≌△DEF,
∵∠C=∠F=90°;
(3)∵AC=8cm,DE=10cm,BC=6cm,
∴DE=AB=10cm,
∴△ABC的周长=6+8+10=24cm;
△DEF的面积=×6×8=24cm2.
18.(2021秋•剑川县校级期中)如图,在Rt△ABC中,∠ACB=90゜,∠A=50゜,将其折叠,使点A落在边CB上A′处,折痕为CD.求∠A′DB的度数.
【分析】根据折叠性质得出∠DCA=∠BCD=45°,∠CDA=∠CDA′,求出∠CDA、∠CDA′,根据三角形外角性质求出∠BDC,即可求出答案.
【解答】解:∵将△ACD折叠,使点A落在边CB上A′处,折痕为CD,∠ACB=90°,
∴∠DCA=∠BCD=45°,∠CDA=∠CDA′,
∴∠CDA=180°﹣∠DCA﹣∠A=180°﹣45°﹣50°=85°,
∴∠CDA′=85°,
∵∠BDC=∠A+∠DCA=50°+45°=95°,
∴∠A′DB=∠BDC﹣∠A′DC=95°﹣85°=10°.
19.(2020秋•东台市月考)直线MN和同侧两点AB,在MN上找一点P,使得PA+PB最小.(尺规作图)
【分析】作点B关于MN的对称点B′,则有PB=PB′,根据两点之间线段最短可得,当A、P、B′三点共线时,PA+PB=PA+PB′最短,故AB′与MN的交点即为所求点P.
【解答】解:以点B为圆心,某一长度为半径画弧,交MN于C、D两点,
以点C为圆心,BC为半径画圆,再以点D为圆心,DB为半径画圆,
设两圆的另一个交点为B′,连接AB′,交MN于P,连接PB,如图所示,
点P即为所求作.
20.(2020春•吉安期中)如图,小丽将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,试求△ACD的周长.
(2)如果∠CAD:∠BAD=4:7,求∠B的度数.
【分析】(1)根据轴对称的性质就可以得出BD=AD,就有△ACD的周长AD+AC+CD=BD+CD+AC而求出结论;
(2)设每份为x°,则∠CAD=4x,∠BAD=7x,由BD=AD可以求出∠B=∠BAD=7x,由直角三角形的性质就可以求出结论.
【解答】解:∵△BDE与△ADE成轴对称,
∴BD=AD,∠B=∠BAD.
∵△ACD的周长=AC+AD+CD,
∴△ACD的周长=AC+BD+CD=AC+BC.
∵AC=6cm,BC=8cm,
∴△ACD的周长=6+8=14cm;
(2)设每份为x°,则∠CAD=4x,∠BAD=7x,
∵∠B=∠BAD,
∴∠B=7x,
∵∠B+∠DAB+∠CAD=90°,
∴7x+7x+4x=90,
∴x=5,
∴∠B=35°.
答:∠B的度数是35°.
21.(2018秋•澧县期末)如图,点A、B在直线l的同侧,点B′是B点关于l的对称点,AB′交l于点P.
(1)AB′与AP+PB相等吗?为什么?
(2)在l上再取一点Q,并连接AQ和QB,比较AQ+QB与AP+PB的大小,并说明理由.
【分析】(1)由轴对称的性质,对称点的连线被对称轴垂直平分,可得PB=PB′,即可得证AB′=AP+PB;
(2)连接QB′,由轴对称的性质可得:QB=QB′,然后根据两点之间线段最短(三角形的三边关系)可得:AQ+QB′>AB′,即AQ+QB>AP+PB.
【解答】解:(1)AB′与AP+PB相等,连接BB′,
∵点B′是B点关于l的对称点,
∴l垂直平分线段BB′,
∴PB=PB′,
∴AP+PB′=AP+BP,
即:AB′=AP+BP;
(2)AQ+QB>AP+PB,
连接QB′,如图所示,
∵点B′是B点关于l的对称点,
∴l垂直平分线段BB′,
∴BQ=QB′,
∵AQ+QB′>AB′,
∴AQ+BQ>AB′,
∵AB′=AP+BP,
∴AQ+QB>AP+PB.
22.(2019秋•横县期中)如图所示,已知Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形,使C点落在AB边上的点D、要使点D恰为AB的中点,问在图中还要添加什么条件?(直接填写答案)
(1)写出两条边满足的条件: BC=AB ;
(2)写出两个角满足的条件: ∠ABC=2∠A ;
(3)写出一个除边、角以外的其他满足条件: △BEC≌△AED .
【分析】(1)根据题意可得要使D在中点,则一定有BC=AB,围绕此条件可推出两边满足的条件.
(2)由轴对称的性质可得出两角满足的条件.
(3)可以写全等的条件.
【解答】解:(1)①AB=BC
证明:由轴对称的性质可得:BC=BD,又因为BC=AB=BD
∴可得D在AB的中点位置.
(2)①∠ABC=2∠A.
∵∠C=90°,
∴∠ABC+∠A=90°.
∵∠ABC=2∠A,
∴∠A=30°.
由轴对称的性质得:BC=BD,CE=DE,∠CBE=∠DBE=∠A=30°.
∴△ADE≌△BCE,AD=BC=BD.
即点D在AB的中点;
(3)△BEC≌△AED
证明:∵△BEC≌△AED
∴可得:AD=DB
故证得点D在AB的中点.
23.(2021秋•大同区校级期末)如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q落在线段MN上,点P关于OB的对称点R落在MN的延长线上,若,MN=a,QR=b,其中a<b,试求PN﹣PM的值.(用a和b表示)
【分析】由轴对称的性质可得RN=PN,MQ=MP,于是推出PN﹣PM=QR﹣MN,即可得到答案.
【解答】解:∵点P关于OA的对称点Q落在线段MN上,点P关于OB的对称点R落在MN上,
∴RN=PN,MQ=MP,
∴PN﹣PM=RN﹣MQ,
∴PN﹣PM=(RN+NQ)﹣(MQ+NQ)=QR﹣MN=b﹣a.
24.(2022秋•威县校级月考)如图,在△ABC中,∠CAB=36°,∠B=48°,D,E分别是边AB和BC上的点,△ACE和△ADE关于直线AE对称,CD交AE于点F.
(1)求∠ADC的度数;
(2)求∠DEB的度数.
【分析】(1)直接利用轴对称的性质得出AC=AD,再利用等腰三角形的性质以及三角形内角和定理得出答案;
(2)直接利用轴对称的性质得出EC=ED,再利用等腰三角形的性质以及三角形外角的性质得出答案.
【解答】解:(1)∵△ACE和△ADE关于直线AE对称,
∴AC=AD,
∴∠ACD=∠ADC,
∵∠CAB=36°,
∴∠ADC=∠ACD==72°;
(2)∵△ACE和△ADE关于直线AE对称,
∴EC=DE,
∴∠ECD=∠EDC,
∵∠CAB=36°,∠B=48°,∠ACD=72°,
∴∠DCB=180°﹣36°﹣48°﹣72°=24°,
∴∠ECD=∠EDC=24°,
∴∠DEB=48°.
相关资料
更多









