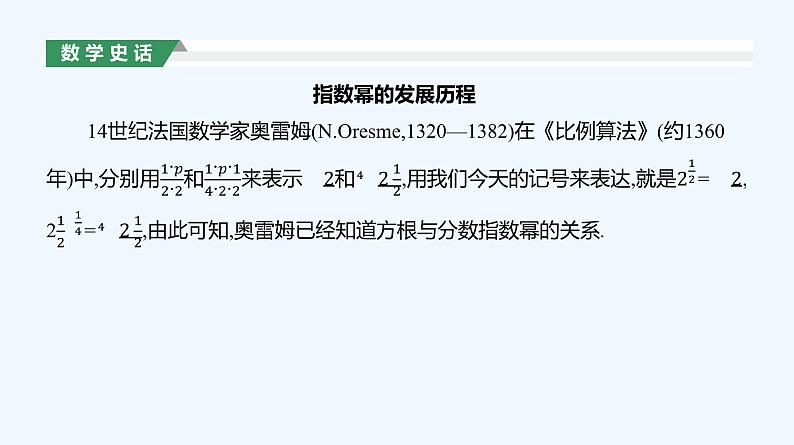
高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.1 指数备课ppt课件

这是一份高中数学人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.1 指数备课ppt课件，共48页。PPT课件主要包含了目标认知，n次方根，一个正数，一个负数，n为偶数，知识点二分数指数幂，没有意义，ar+s，ars，arbr等内容，欢迎下载使用。

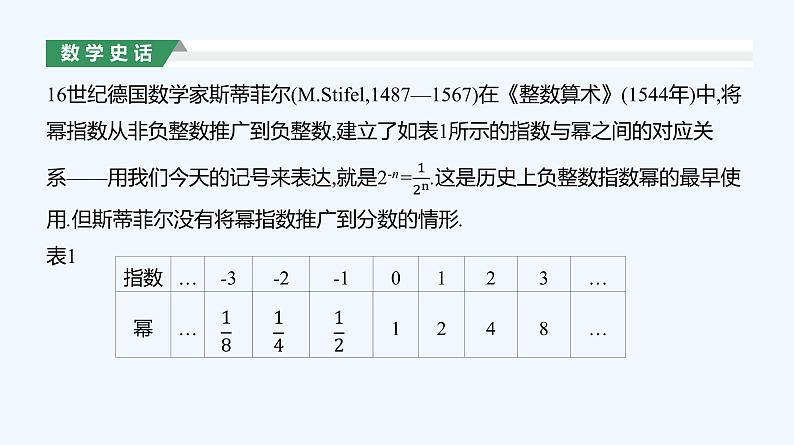
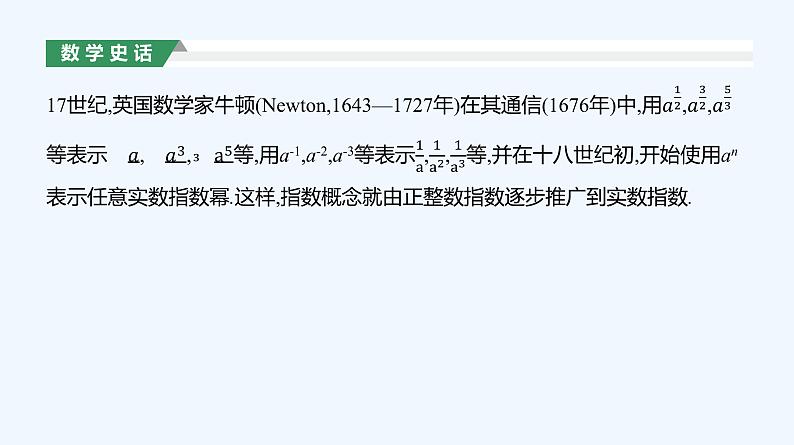
17世纪英国数学家沃利斯(J.Wallis,1616—1703)在《无穷算数》(1655)中给出负数指数幂和分数指数幂的运算,从而将正整数指数幂的运算律推广到了任意有理数指数幂.　　1637年,法国数学家笛卡儿(Descartes,1596—1650年)开始用符号an表示正整数幂,在他的《几何学》一书中,用a3代表aaa,用a4代表aaaa.
知识点一　根式的概念及其性质
1.n次方根一般地,如果xn=a,那么x叫作a的　　　　　　.其中n>1,且n∈N* .式子　 　　叫作根式,这里n叫作根指数,a叫作被开方数. (1)当n为奇数时,正数的n次方根是　　 　　,负数的n次方根是　　 　　.这时,a的n次方根用符号　　　　表示. 
[解析] (1)根据n次方根的定义知,任意实数的奇次方根只有1个.
[解析] (2)当n为大于1的偶数时,实数a的n次方根有0个或1个或2个.
3.有理数指数幂的运算性质(1)aras=　　　　(a>0,r,s∈Q); (2)(ar)s=　　　　(a>0,r,s∈Q); (3)(ab)r=　　　　(a>0,b>0,r∈Q). 
知识点三　无理数指数幂
1.无理数指数幂aα(a>0,α为无理数)是一个确定的实数.2.实数指数幂的运算性质(1)aras=　　　　(a>0,r,s∈R); (2)(ar)s=　　　　(a>0,r,s∈R); (3)(ab)r=　　　　(a>0,b>0,r∈R). 
1.分数指数幂(1)分数指数幂不表示相同因式的乘积,而是根式的另一种写法,分数指数幂与根式可以相互转化,在把偶数次根式化成分数指数幂时,要注意使底数大于0.同时,负数开奇数次方根是有意义的,所以当奇数次根式化成分数指数幂时,先要把负号移到根号外面去,然后再按规定化成分数指数幂.(2)负分数指数幂在有意义的情况下总表示正数,而不是负数,负号只是出现在指数上.
2.实数指数幂引入了分数指数幂后,指数概念就实现了由整数指数幂向有理数指数幂的扩充.当a>0,p是一个无理数时,规定ap表示一个确定的实数,而且有理数指数幂的运算性质对于无理数指数幂也适用,这样,指数概念就扩充到了整个实数范围.
探究点一　n次方根的概念
探究点二　根式的化简与求值
[素养小结]根式化简的思想是利用乘法公式将被开方数变形为幂的形式,用根式的性质将根式化简,解题时要注意公式的适用范围,特别是在化简含有字母的根式时要注意字母的取值范围.
探究点三　根式与分数指数幂互化
探究点四　实数指数幂的运算
[素养小结](1)基本原则:式子里既有指数幂又有根式时,一般把根式统一化为指数幂的形式,再利用指数幂的运算性质化简.(2)常规方法: ①化负指数幂为正指数幂;②化根式为分数指数幂;③化小数为分数.
2.解决此类问题的一般步骤:
1.指数式的化简与求值(1)一般地,进行指数幂运算时,化负指数为正指数、化根式为分数指数幂、化小数为分数进行运算,便于进行乘除、乘方、开方运算,可以达到化繁为简的目的.(2)对“条件求值”问题一定要弄清已知与未知的联系,然后采取“整体代换”或“求值后代换”两种方法求值.
2.“凑公式”法在本节的试题中,有些式子直接计算比较麻烦,此时我们要善于观察所求式子的结构特征,“凑”出乘法公式或因式分解公式的形式,充分利用这些公式进行幂的综合运算.