





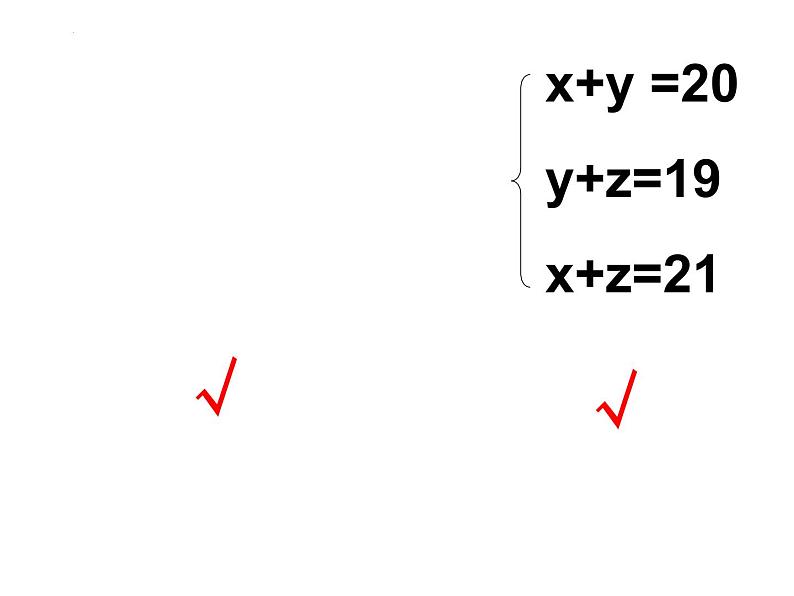
还剩10页未读,
继续阅读
初中数学人教版七年级下册8.4 三元一次方程组的解法集体备课ppt课件
展开
这是一份初中数学人教版七年级下册8.4 三元一次方程组的解法集体备课ppt课件,共18页。PPT课件主要包含了二元一次方程组,一元一次方程,消元的方法,代入法,加减法,合作研讨,你给它起个名字吧,基本思想,三元一次方程组,解法探究等内容,欢迎下载使用。
1、什么是二元一次方程组?
有两个未知数,含有未知数项的次数都是1,并且一共有两个方程的方程组,叫二元一次方程组。
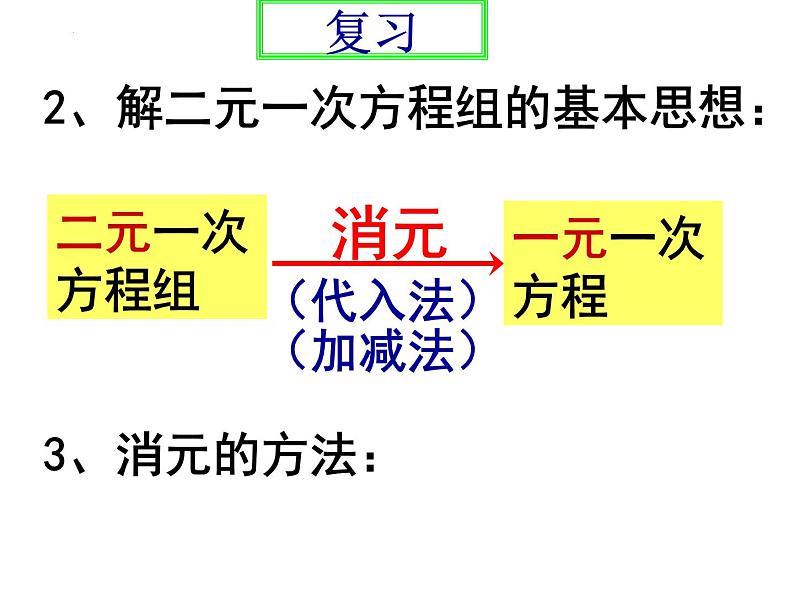
2、解二元一次方程组的基本思想:
1、你可以设几个未知数?
问题:小明手头有12张面额分别1元、2元、5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍.求1元、2元、5元纸币各多少张?
2、你可以找到几个等量关系?
3、请你列方程解决这个问题
解:设1元、2元、5元的纸币分别为x张、y张、z张。
这个方程组是二元一次方程组吗?为什么?
三元一次方程组的定义:
类比二元一次方程组,请给三元一次方程组下个定义吧
判断下列方程组是不是三元一次方程组?
怎样解三元一次方程组?
解三元一次方程组的基本思想:
例1:解三元一次方程组:
当方程组中有形如:x=4y这样,用一个字母表示另一个字母的方程时,可优先选择代入法消元
练习1:解三元一次方程组:
例2:解三元一次方程组:
当方程组中只有一个二元一次方程时,可由它决定消元字母(缺某元,消某元),并将另两个方程进行加减消元。
练习2:解三元一次方程组:
练习3:解三元一次方程组:
例3:在等式y=ax2 +bx+c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60。求a、b、c的值。
25a+5b+c=60
1、不解方程组,指出下列方程组中先消去哪个未知数,使得求解方程组较为简便?
2解方程组 若要使运算简便,消元的方法应选取( )(A)先消去x; (B)先消去y;(C)先消去z; (D)以上说法都不对
1、什么是二元一次方程组?
有两个未知数,含有未知数项的次数都是1,并且一共有两个方程的方程组,叫二元一次方程组。
2、解二元一次方程组的基本思想:
1、你可以设几个未知数?
问题:小明手头有12张面额分别1元、2元、5元的纸币,共计22元,其中1元纸币的数量是2元纸币数量的4倍.求1元、2元、5元纸币各多少张?
2、你可以找到几个等量关系?
3、请你列方程解决这个问题
解:设1元、2元、5元的纸币分别为x张、y张、z张。
这个方程组是二元一次方程组吗?为什么?
三元一次方程组的定义:
类比二元一次方程组,请给三元一次方程组下个定义吧
判断下列方程组是不是三元一次方程组?
怎样解三元一次方程组?
解三元一次方程组的基本思想:
例1:解三元一次方程组:
当方程组中有形如:x=4y这样,用一个字母表示另一个字母的方程时,可优先选择代入法消元
练习1:解三元一次方程组:
例2:解三元一次方程组:
当方程组中只有一个二元一次方程时,可由它决定消元字母(缺某元,消某元),并将另两个方程进行加减消元。
练习2:解三元一次方程组:
练习3:解三元一次方程组:
例3:在等式y=ax2 +bx+c中,当x=-1时,y=0;当x=2时,y=3;当x=5时,y=60。求a、b、c的值。
25a+5b+c=60
1、不解方程组,指出下列方程组中先消去哪个未知数,使得求解方程组较为简便?
2解方程组 若要使运算简便,消元的方法应选取( )(A)先消去x; (B)先消去y;(C)先消去z; (D)以上说法都不对













