













- 4.4 用待定系数法确定一次函数表达式 课件+教案+PPT练习+素材 课件 10 次下载
- 4.5 一次函数的应用(3课时)课件+教案+PPT练习 课件 9 次下载
- 5.1 频数与频率 课件+教案+PPT练习 课件 7 次下载
- 5.2 频数直方图 课件+教案+PPT练习 课件 7 次下载
- 5 章末复习 课件+教案 课件 9 次下载
4 章末复习(2课时) 课件+教案
展开章末复习
【知识与技能】
使学生理解一次函数的意义,掌握根据条件确定一次函数表达式的方法,会画一次函数图象.探究并掌握一次函数性质,并用之解决实际问题.
【过程与方法】
通过例题讲解,学会一次函数性质及应用.
【情感态度】
体会函数作为数学模型在分析解决实际问题中的重要作用.
【教学重点】
应用一次函数的概念、图象和性质解题.
【教学难点】
一次函数在实际问题中的应用.
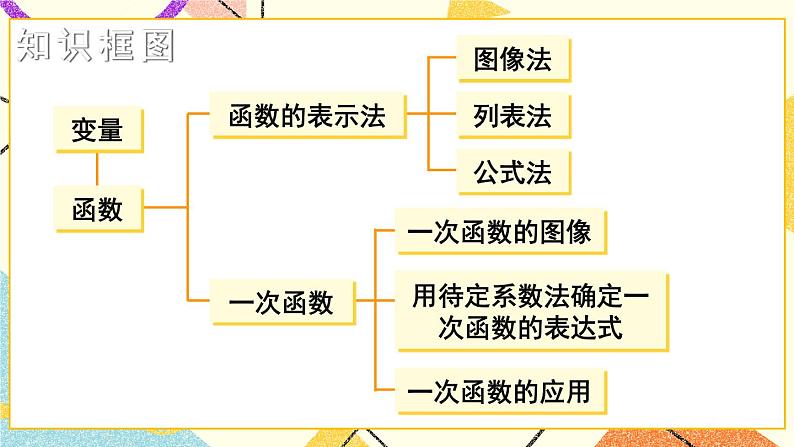
一、知识框图,整体把握
【教学说明】引导学生回顾本章知识点,展示结构框图,让学生对所学知识有个系统地了解,教学时,可以边回顾边构建结构图,逐步加深印象.
二、释疑解惑,加深理解
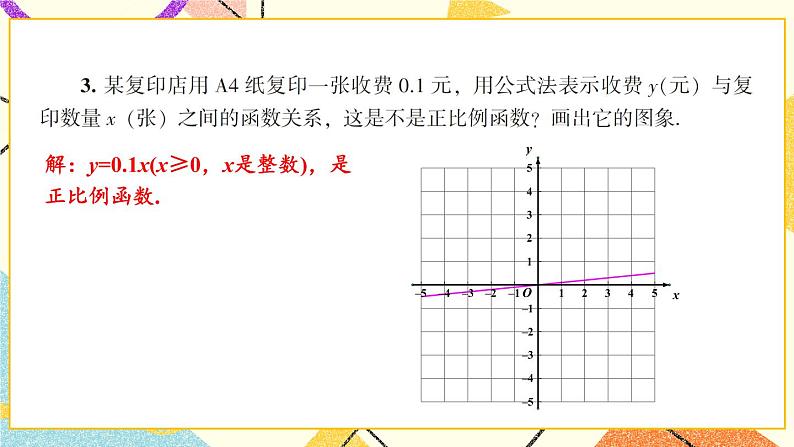
1.在研究函数问题时,要专注函数自变量的取值范围,函数表达式本身以及实际问题中自变量代表的意义对自变量有所限制,不可忽视.
2.在本章学习过程中,我们经历了从具体情境中抽象出数学问题,用函数表达式表示问题中的数量关系,进而得到函数模型这一过程,注意体会函数是刻画现实世界数量关系的有效模型.
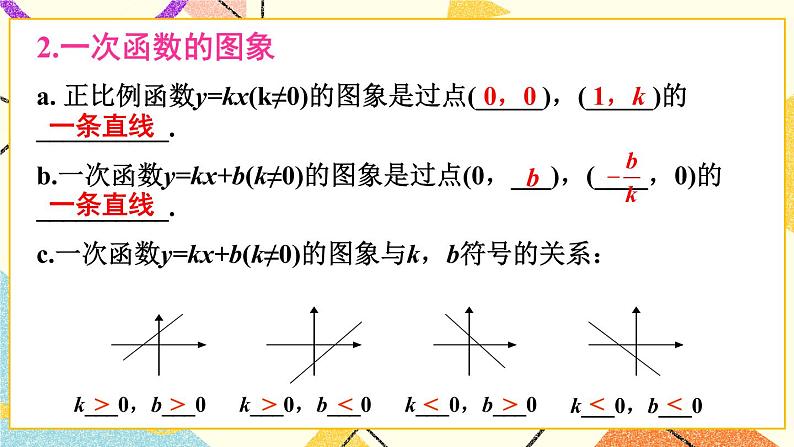
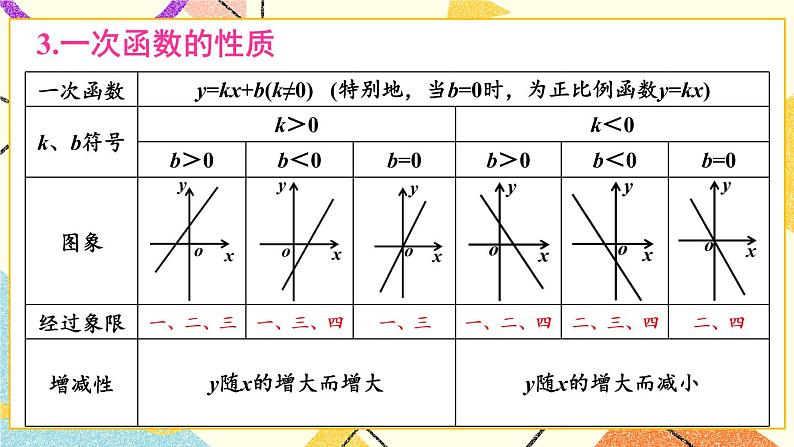
3.对于一次函数,通过图象可以数形结合地研究函数,有助于全面掌握函数的特征以及利用性质解决问题.
三、典例精析,复习新知
例1 函数中自变量x的取值范围是( )
A.x≥1且x≠3 B.x≥1 C.x≠3 D.x>1且x≠3
【分析】根据题意得,x-1≥0且x-3≠0,解得x≥1且x≠3,故选A.
例2 某人匀速跑步到公园,在公园里某处停留了一段时间,再沿原路匀速步行回家,此人离家的距离y与时间x的关系的大致图象是( )
【分析】根据每段中离家的距离随时间的变化情况即可进行判断,故选B.
例3 (1)正比例函数y=1/2x的图象经过第 象限,y随x的增大而 ;
(2)已知y=(2m-1)是正比例函数,且y随x的增大而减小,则m的值是 .
【分析】(1)因为k=1/2>0,所以由正比例函数的性质可知,它的图象经过第一、三象限,y随x的增大而增大;(2)y=(2m-1)是正比例函数的条件是m2-3=1且2m-1≠0,要使y随x的增大而减小还应满足条件2m-1<0,综合这些条件得:当m2-3=1,2m-1<0时,y=(2m-1) y=(2m-1)是正比例函数,且y随x的增大而减小,故(1)一、三;增大;(2)-2.
例4 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发驶向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系,请根据图象解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式.
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求轿车从甲地出发后多长时间再与货车相遇(结果精确到0.01).
【分析】(1)先求出货车的速度,再根据货车迟到0.5小时求解;(2)运用待定系数法求解;(3)设轿车从甲地出发x小时后再与货车相遇,根据轿车(x-4.5)小时行驶的路程+货车x小时行驶的路程=300千米列出方程,即可求解.
解:(1)根据图象信息:货车的速度V货=3005=60(千米/时),由图象可知货车比轿车迟到0.5小时,∴此时货车距乙地的路程为0.5×60=30(千米);(2)设CD段函数解析式为y=kx+b(k≠0)(2.5≤x≤4.5).∵C(2.5,80),D(4.5,300)在其图象上,∴2.5k+b=80,4.5k+b=300,解得k=110,b=-195.∴CD段函数解析式为:y=110x-195(2.5≤x≤4.5);(3)设轿车从甲地出发x小时后再与货车相遇,∵v货车=60千米/时,v轿车=300-804.5-2.5=110(千米/时)∴110(x-4.5)+60x=300,解得x≈4.68(小时).答:轿车从甲地出发约4.68小时后再与货车相遇.
【教学说明】典型例题的分析,对学生解题起着非常重要的指导作用,教师在讲评的过程中有必要让学生明白本章的重点有哪些,需要注意些什么问题,逐步熟能生巧.
四、复习训练,巩固提高
1.根据下图所示程序计算函数值,若输出的函数值为4/25,则输入的x的值为( )
A.29/25 B.±2/5 C.2/5 D.25/4
2.函数y1=|x|,y2=1/3x+4/3,当y1>y2时,x的范围是( )
A.x<-1 B.-1<x<2 C.x<-1或x>2 D.x>2
3.(0,1)向下平移2个单位后的坐标是 ,直线y=2x+1向下平移2个单位后的解析式是 .直线y=2x+1向右平移2个单位后的解析式是 .
4.星期天8:00~8:30,燃气公司给平安加气站的储气罐注入天然气.之后,一位工作人员以每车20立方米的加气量,依次给在加气站排队等候的若干辆车加气.储气罐中的储气量y(立方米)与时间x(小时)的函数关系如图所示.
(1)8:00~8:30,燃气公司向储气罐注入了多少立方米的天然气?
(2)当x≥0.5时,求储气罐中储气量y(立方米)与时间x(小时)的函数解析式;
(3)请你判断,正在排队等候的第18辆车能否在当天10:30之前加完气?请说明理由.
【教学说明】这部分安排了本章几个重点知识的运用,目的是为了检验学生的掌握程度,便于及时查漏补缺.
【答案】1.C 2.C 3.(0,-1),y=2x-1,y=2x-3
4.解:(1)由图可知,星期天8:00~8:30,注入了10000-2000=8000立方米的天然气.
(2)当x≥0.5时,储气罐中的储气量y(立方米)与时间x(小时)的函数解析式为y=-200x+10100.(3)可以,∵给18辆车加气需18×20=360(立方米),储气量为10000-360=9640(立方米),于是有:9640=-20x+10100,解得x=2.3,而从8:00到10:30相差2.5小时,显然有:2.3<2.5,故第18辆车在当天10:30之前可以加完气.
五、师生互动,课堂小结
本节课你能完整回顾本章所学过的一次函数的相关的知识吗?你认为哪些内容是大家要掌握的?还有哪些方面的疑难问题?请与大家共同讨论.
【教学说明】通过师生共同回顾本章知识,放手让学生自由讨论、交流形成共识,欠缺的地方教师做必要的补充强调.
1.布置作业:从复习题中选取.
2.完成练习册中“本章重点知识专项训练”.
本节课从归纳本章主要内容入手,以精选例题为范本,学生的实际运用为主线,通过学生的归纳整理使本章所学内容进一步深化,能力逐渐提高.









