5 章末复习 课件+教案

章末复习

【知识与技能】

1.通过回顾思考本章内容，进一步理解频数、频率的概念及数据值的频数分布和频数分布直方图.

2.能够准确地计算数据的频数和频率，会分析频数分布表和频数分布直方图，获得相关信息解决简单问题.

【过程与方法】

经历收集、处理数据的过程，进一步了解频数与频率在实际生活中的应用，通过绘图，进一步掌握数形结合的思想方法.

【情感态度】

培养学生的交流与合作能力，感受成功的体验，激发学生对数学的兴趣.对学生进行由实践到理论，由理论到实践的认识规律的教育.

【教学重点】

理解频数、频率等概念，能绘制相应的频数分布直方图.

【教学难点】

观察、整理和归纳能力的培养.

一、    知识框图，整体把握

【教学说明】引导学生回顾本章所学知识点，展示本章结构框图，让学生对本章知识有个系统地了解，教学时，可以边回顾边构建结构图，有助于加深印象.

二、释疑解惑，加深理解

1.平均数、中位数、众数、方差是描述一组数据在某些方面的特征性质，而频数直方图是反映一组数据中各数据在不同范围的分布情况，在实际问题中要具体情况具体对待.

2.绘制频数直方图时，要注意组距的选取，若组距选择太密，则从直方图中无法读取有用的信息，若组距选择太窄，则直方图中可获取的信息少.

3.频数直方图本质上是一种条形统计图，要体会它与条形统计图的区别与联系.

三、典例精析，复习新知

例1  某市对2400名年龄满15岁的男生的身高进行了测量，结果身高（单位：m）在1.68~1.70这一小组的频率为0.25，则该组的人数为（    ）

A.600         B.150          C.60           D.15

【分析】根据频数=频率×数据总和进行计算.

解：由题意得：该组的人数为：2400×0.25=600（人），故选A.

例2  有5条线段长度分别为1，2，3，5，7，从中选取任意三条为一组，它们一定能构成三角形的频率为       .

【分析】先求出5条线段中的任意3条一组，共有多少组，再求出能构成三角形的有几种，根据频率分式即可求解.

解：5条线段中的任意3条为一组，共有1，2，3；1，2，5；1，2，7；1，3，5；1，3，7；1，5，7；2，3，5；2，5，7；3，5，7共10种，其中能构成三角形的有3，5，7一种，所以一定能构成三角形的频率是1÷10=0.1，故填0.1.

例3  当前，“校园手机”现象已经受到社会广泛关注，某数学兴趣小组对“是否赞成中学生带手机进校园”的问题进行了社会调查，小文将调查数据作出如下不完整的整理：

（1）请求出共调查了多少人；并把小文整理的图表补充完整；

（2）小丽要将调查数据制成扇形统计图，则扇形统图中“赞成”的圆心角是多少度？

【分析】（1）首先用反对的频数除以反对的频率得到调查的总人数，然后求无所谓的人数和赞成的频率即可；（2）赞成的圆心角等于赞成的频率乘360°即可.

解：（1）观察统计表知道：反对的频数为40，频率为0.8，故调查的人数为：40÷0.8=50（人）；无所谓的频数为：50-5-40=5（人），赞成的频率为：1-0.1-0.8=0.1；

统计图为：

（2）∵赞成的频率为0.1，∴“赞成”的圆心角是360°×0.1=36°.

【教学说明】典型例题的分析，对学生解题起着非常重要的指导作用，教师在讲评的过程中有必要让学生明白本章的重点有哪些，需要注意什么问题，能力逐步提高.

四、复习训练，巩固提高

1.我校八年级学生在生物实验中抽出50粒种子进行研究，数据落在37~40之间的频率是0.2，则这50个数据在37~40之间的个数是（）A.1B.2C.10D.52.有40个数据，其中最大值为35，最小值为15，若取组距为4组，则应该分的组数是（    ）

A.4           B.5           C.6            D.7

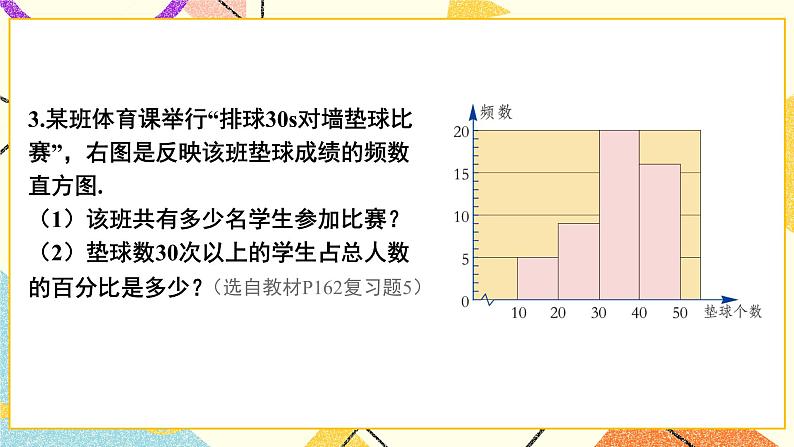
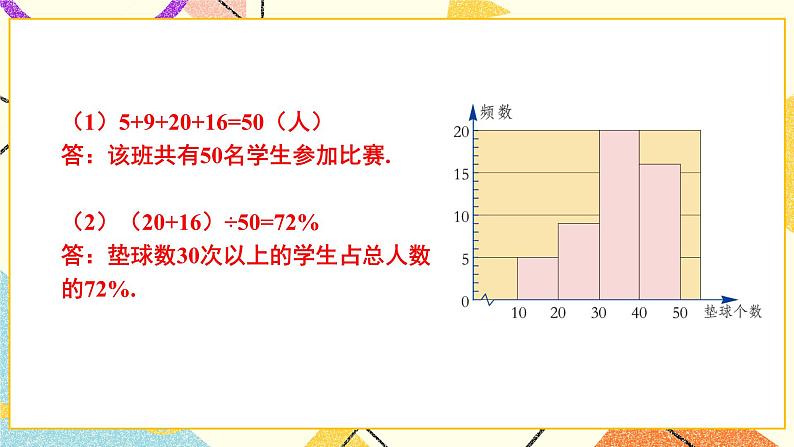
3.某校为了解九年级学生的体能情况，随机抽查了其中的30名学生，测试了1分钟仰卧起坐的次数，并绘制成如图的频数分布直方图，则仰卧起坐次数在20~25之间的频数是.

4.为增强学生的身体素质，教育行政部门规定学生每天户外活动的平均时间不少于1小时，为了解学生参加户外活动的情况，对部分学生参加户外活动的时间进行抽样调查，并将调查结果绘制成如图中两幅不完整的统计图，请你根据图中提供的信息解答下列问题：

（1）在这次调查中共调查了多少名学生？

（2）求户外活动时间为0.5小时的人数，并补充频数分布直方图；

（3）求表示户外活动时间为2小时的扇形圆心角的度数；

（4）本次调查中学生参加户外活动的平均时间是否符合要求？户外活动时间的众数和中位数各是多少？

【教学说明】这部分安排了本章几个重点知识的运用，目的是为了检验学生的掌握程度，便于及时查漏补缺.

【答案】1.C    2.B     3.10

4.解：（1）调查学生人数：32÷40%=80（人）；

（2）0.5小时的人数是：80×20%=16（人）；频数分布直方图如图所示：

（3）表示户外活动时间2小时的扇形圆心角的度数12÷80×360°=54°；

（4）户外活动的平均时间（16×0.5+32×1+20×1.5+12×2）÷80=1.175（小时），∵1.175>1，∴平均活动时间符合要求；户外活动时间的众数和中位数均为1.

五、师生互动，课堂小结

本节课你能完整地回顾本章所学的与频数频率有关的知识吗？你认为哪些内容是大家要掌握的？需要注意哪方面的问题？还有什么疑难问题？请与大家共同讨论.

【教学说明】通过师生共同回顾本章所学知识，大胆让学生合作交流，讨论达成共识，欠缺的地方教师作必要的补充说明.

1.布置作业：从复习题中选取.

2.完成练习册.

本节课从归纳总结本章主要内容入手，以精选的例题为范本，学生的加强练习为主线，通过学生的整理让本章所学内容全面得到深化，能力逐渐提高.