初中18.2.2 菱形教课内容课件ppt

这是一份初中18.2.2 菱形教课内容课件ppt，共22页。

知识点一　 菱形的性质1.菱形不具备的性质是( )A.四条边都相等　　 B.对角线一定相等C.是轴对称图形 D.是中心对称图形
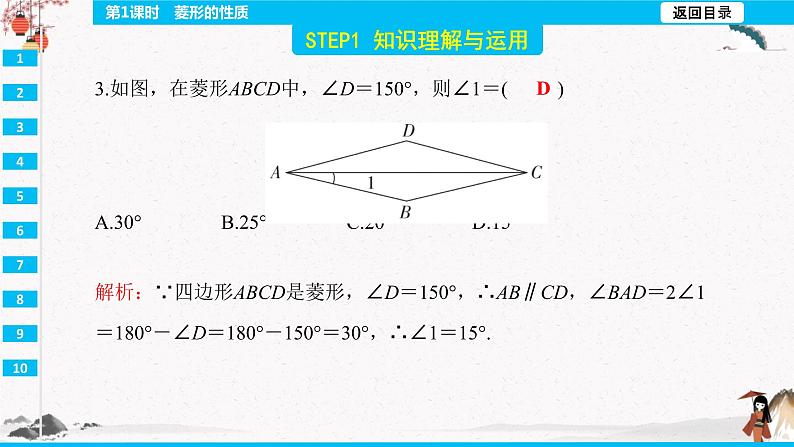
D 解析：∵四边形ABCD是菱形，∠D＝150°，∴AB∥CD，∠BAD＝2∠1＝180°－∠D＝180°－150°＝30°，∴∠1＝15°.
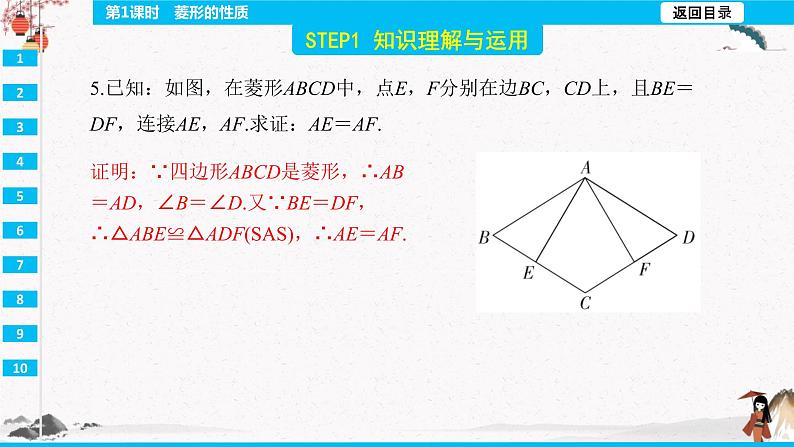
证明：∵四边形ABCD是菱形，∴AB＝AD，∠B＝∠D.又∵BE＝DF，∴△ABE≌△ADF(SAS)，∴AE＝AF.
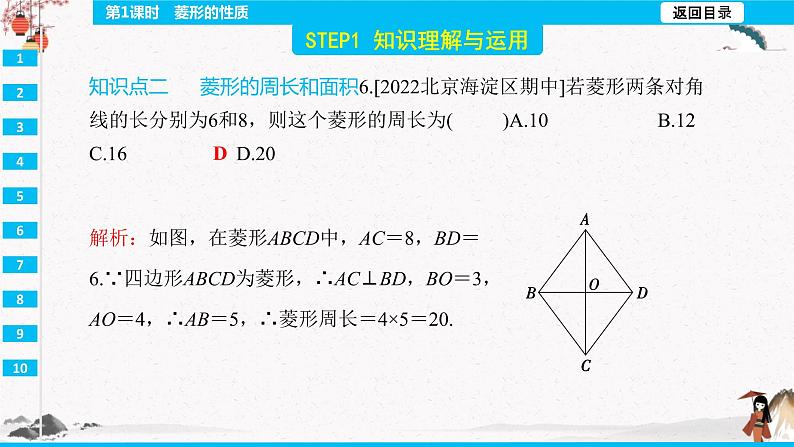
知识点二　 菱形的周长和面积6.[2022北京海淀区期中]若菱形两条对角线的长分别为6和8，则这个菱形的周长为( )A.10 B.12 C.16 D.20
16 解析：∵四边形ABCD为菱形，∴AC⊥BD，AB＝BC＝CD＝DA，∴∠COD＝90°.∵OE＝2，且E为CD边的中点，∴CD＝2OE＝4，∴菱形ABCD的周长＝4CD＝4×4＝16.
9.[2022广东广州海珠区一模]菱形的两个内角的度数比是1∶3，一边上的高长是4，则菱形的面积是　　　　.
(－2，4) 解析：∵点C的坐标是(3，4)，∴OC＝5.∵四边形OABC为菱形，∴BC＝OC＝5，则点B的坐标为(－2，4).
解：(1)∵四边形ABCD是菱形，∴AB＝BC.∵∠ABC＝60°，∴△ABC是等边三角形，∴∠BCA＝60°.∵E是线段AC的中点，∴∠CBE＝∠ABE＝30°，AE＝CE.