第十八章 单元学考对接 同步典型例题精讲课件

这是一份第十八章 单元学考对接 同步典型例题精讲课件，共53页。

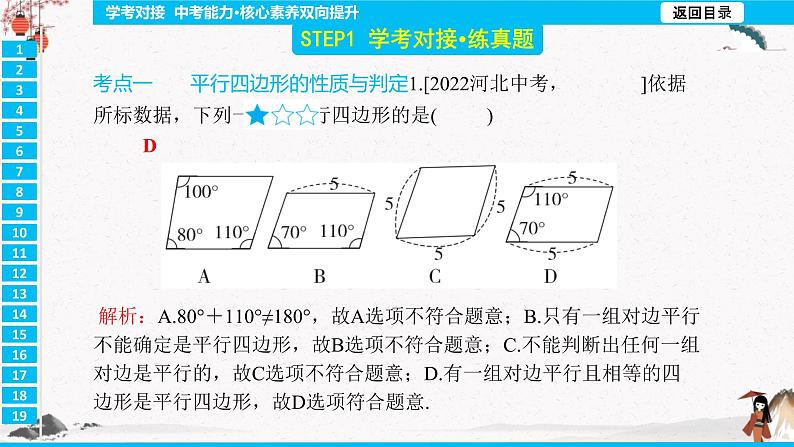
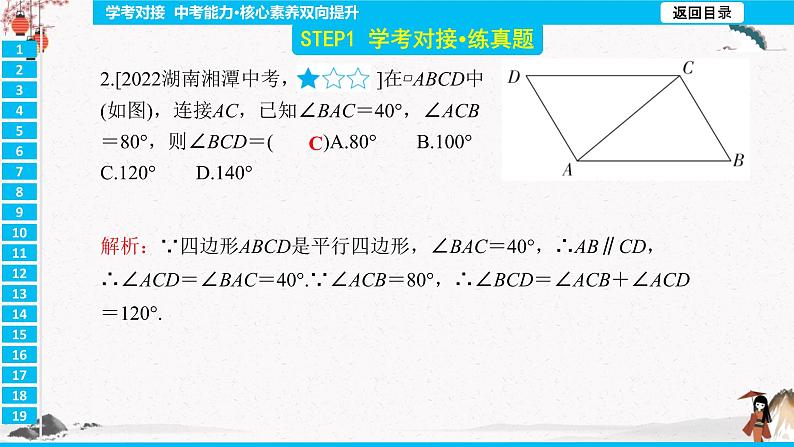
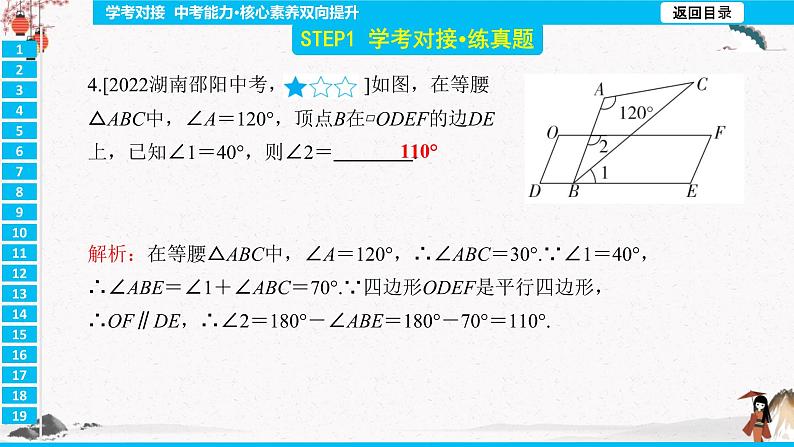
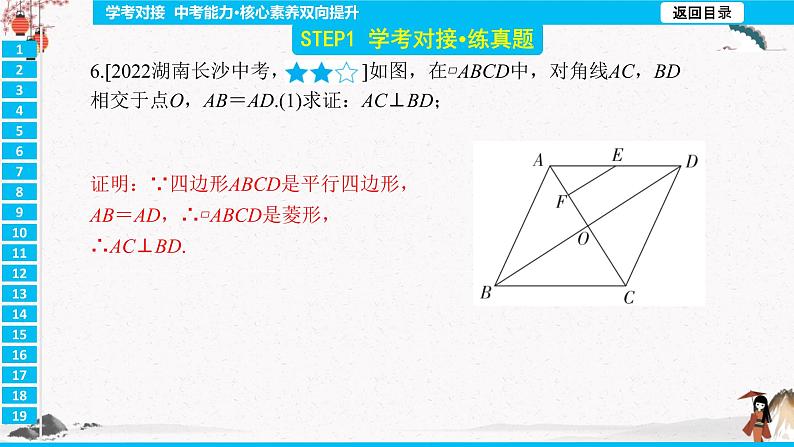
第十八章 平行四边形 D 解析：A.80°＋110°≠180°，故A选项不符合题意；B.只有一组对边平行不能确定是平行四边形，故B选项不符合题意；C.不能判断出任何一组对边是平行的，故C选项不符合题意；D.有一组对边平行且相等的四边形是平行四边形，故D选项符合题意. C 解析：∵四边形ABCD是平行四边形，∠BAC＝40°，∴AB∥CD，∴∠ACD＝∠BAC＝40°.∵∠ACB＝80°，∴∠BCD＝∠ACB＋∠ACD＝120°. B 解析：∵EF∥AC，GF∥AB，∴四边形AEFG是平行四边形，∠B＝∠GFC，∠C＝∠EFB.∵AB＝AC，∴∠B＝∠C，∴∠B＝∠EFB，∠GFC＝∠C，∴EB＝EF，FG＝GC，∴四边形AEFG的周长＝AE＋EF＋FG＋AG＝AE＋EB＋GC＋AG＝AB＋AC＝8＋8＝16. 110° 解析：在等腰△ABC中，∠A＝120°，∴∠ABC＝30°.∵∠1＝40°，∴∠ABE＝∠1＋∠ABC＝70°.∵四边形ODEF是平行四边形，∴OF∥DE，∴∠2＝180°－∠ABE＝180°－70°＝110°. (－2，－1) 解析：∵四边形ABCD为平行四边形，且A(－1，2)，D(3，2)，∴点A是点D向左平移4个单位长度所得.∵C(2，－1)，∴B(－2，－1).证明：∵四边形ABCD是平行四边形，AB＝AD，∴▱ABCD是菱形，∴AC⊥BD.定四边形ADFC为平行四边形，故本选项不符合题意；D.∵AD＝CF，AD＝BD，∴BD＝CF.由BD＝CF，∠BED＝∠CEF，BE＝CE，不能判定△BED≌△CEF，不能判定CF∥AB，即不能判定四边形ADFC为平行四边形，故本选项不符合题意. 20 解析：∵D，E分别是AC，BC的中点，∴DE是△ABC的中位线，∴AB＝2DE＝2×10＝20 (m). C 解析：在Rt△ABC中，∠ABC＝90°，点D为边AC的中点，BD＝2，∴BD＝CD＝AD.∵∠C＝60°，∴△BCD是等边三角形，∴BC＝BD＝2. D 解析：A.在▱ABCD中，AB＝AC，不能判定▱ABCD是矩形，故选项A不符合题意；B.∵在▱ABCD中，AC⊥BD，∴▱ABCD是菱形，故选项B不符合题意；C.∵在▱ABCD中，AB＝AD，∴▱ABCD是菱形，故选项C不符合题意；D.∵在▱ABCD中，AC＝BD，∴▱ABCD是矩形，故选项D符合题意.D只要MN⊥EF，OM＝ON，则四边形MENF就是菱形.∵点E，F是BD上的动点，∴存在无数个菱形MENF，故③正确；只要MN＝EF，MN⊥EF，OM＝ON，则四边形MENF就是正方形，而符合要求的正方形只有一个，故④错误.C2.在平行四边形ABCD中，∠A＋∠C＝110°，则∠B＝( )A.70° B.110° C.125° D.130° C 解析：在▱ABCD中，∠A＝∠C，∠A＋∠C＝110°，∴∠A＝∠C＝55°，∴∠B＝180°－∠A＝125°.A7.四边形ABCD的对角线AC＝BD，AC⊥BD，分别过点A，B，C，D作对角线的平行线，所成的四边形EFMN是( )A.正方形 B.菱形 C.矩形 D.任意四边形 C 解析：∵DE∥BC，EF∥AB，∴∠DEB＝∠EBF，四边形DBFE是平行四边形.∵BE平分∠ABC，∴∠DBE＝∠EBF，∴∠DBE＝∠DEB，∴DB＝DE，∴四边形DBFE是菱形，故方案甲正确；∵DE＝BF，BD＝EF，∴四边形DBFE是平行四边形，故方案乙错误；∵BD＝DE＝EF＝FB，∴四边形DBFE是菱形，故方案丙正确.DA90°解：∵四边形ABCD是平行四边形，∴AB∥CD，∴∠B＋∠C＝180°.∵∠B＝60°，∴∠C＝120°.∵AE⊥BC，AF⊥CD，∴∠AEC＝∠AFC＝90°.在四边形AECF中，∠EAF＋∠AEC＋∠C＋∠AFC＝360°，∴∠EAF＝60°.解：(1)证明：∵四边形ABCD是正方形，∴∠BAD＝90°，AC平分∠BAD.∵PM⊥AD，PN⊥AB，∴PM＝PN，∠PMA＝∠PNA＝90°，∴四边形PMAN是矩形.又∵PM＝PN，∴四边形PMAN是正方形.(2)∵四边形PMAN是正方形，∴∠APM＝45°，∠AMP＝90°.∵∠APE＝15°，∴∠EPM＝30°，∴∠MEP＝60°.解：(1)二.(2)证明：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠FAC＝∠ECA.∵EF是AC的垂直平分线，∴EF⊥AC，OA＝OC，∠AOF＝∠COE＝90°，∴△AOF≌△COE(ASA)，∴FO＝EO，∴四边形AECF是平行四边形.∵EF⊥AC，∴四边形AECF是菱形.解：(1)证明：在等边△BCE和等边△ABF中，BE＝BC，BF＝BA.又∵∠FBE＝60°－∠ABE，∠ABC＝60°－∠ABE,∴∠FBE＝∠ABC，在△BFE和△BAC中，