第八章　章末整合课件PPT

这是一份第八章　章末整合课件PPT，共33页。

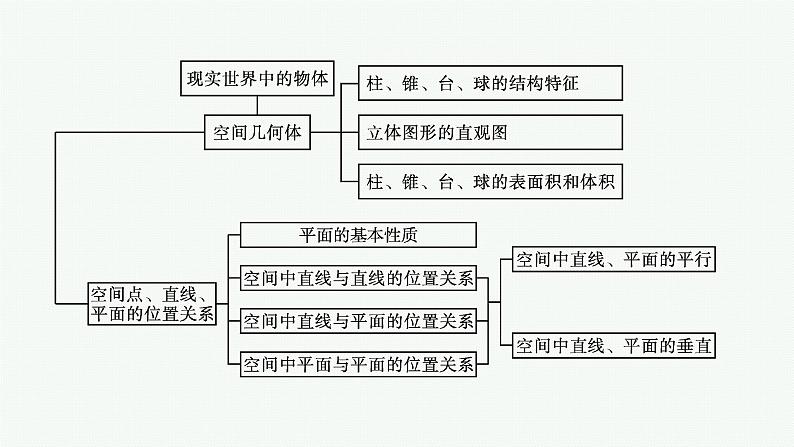
高中同步学案优化设计GAO ZHONG TONG BU XUE AN YOU HUA SHE JI第八章2022内容索引知识网络系统构建题型突破深化提升知识网络系统构建空间平行、垂直关系之间的转化 题型突破深化提升例1根据下列对几何体结构特征的描述,说出几何体的名称.(1)由六个面围成,其中一个面是凸五边形,其余各面是有公共顶点的三角形;(2)一个等腰梯形绕着两底边中点的连线所在的直线旋转180°形成的面所围成的旋转体;(3)一个直角梯形绕较长的底边所在的直线旋转一周形成的面所围成的旋转体.解 (1)如图①,因为该几何体的五个面是有公共顶点的三角形,所以是棱锥,又其底面是凸五边形,所以是五棱锥.(2)如图②,等腰梯形两底边中点的连线将梯形平分为两个直角梯形,每个直角梯形旋转180°形成半个圆台,故该几何体为圆台.(3)如图③,过直角梯形ABCD的顶点A作AO⊥CD于点O,将直角梯形分为一个直角三角形AOD和一个矩形AOCB,绕CD旋转一周形成一个组合体,该组合体由一个圆锥和一个圆柱组成.名师点析与空间几何体结构特征有关问题的解题技巧(1)紧扣结构特征是判断的关键,熟悉空间几何体的结构特征,依据条件构建几何模型,在条件不变的情况下,变换模型中的线面关系或增加线、面等基本元素,然后再依据题意判定.(2)通过举反例对结构特征进行辨析,要说明一个命题是错误的,只要举出一个反例即可.变式训练1给出下列四种说法:①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;②底面为正多边形,且相邻两个侧面与底面垂直的棱柱是正棱柱;③直角三角形绕其任一边所在直线旋转一周所形成的旋转体都是圆锥;④棱台的上、下底面可以不相似,但侧棱长一定相等.其中正确的个数是(　　)A.0 B.1 C.2 D.3答案 B解析 ①上、下底面的圆周上两点的连线要与轴平行才是母线;③直角三角形绕着直角边所在直线旋转一周才能形成圆锥;④棱台的上、下底面相似,侧棱长不一定相等.故只有②正确.例2如图所示,在边长为4的正三角形ABC中,E,F依次是AB,AC的中点,AD⊥BC,EH⊥BC,FG⊥BC,D,H,G为垂足.若将△ABC中的四边形EFGH抠掉后,剩余部分绕AD所在直线旋转180°,求形成的几何体的表面积与体积.解 所得几何体是由一个圆锥挖去一个圆柱后形成的,∵S锥表=π·DC2+π·DC·AC=4π+8π=12π, 名师点析(1)空间几何体表面积的求法①多面体的表面积是各个面的面积之和;组合体的表面积注意衔接部分的处理.②旋转体的表面积问题注意其侧面展开图的应用.(2)空间几何体体积问题的常见类型及解题策略①若所给定的几何体是可直接用公式求解的柱体、锥体或台体,则可直接利用公式进行求解.②若所给定的几何体的体积不能直接利用公式得出,则常用转换法、分割法、补形法等方法进行求解.特别地,求三棱锥体积时经常要转换顶点和底面,从而达到方便求高的目的.变式训练2如图所示,已知三棱柱ABC-A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥B1-ABC1的体积为(　　)答案 A 例3如图,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.求证:(1)平面ADE⊥平面BCC1B1;(2)直线A1F∥平面ADE.(1)证明 因为三棱柱ABC-A1B1C1是直三棱柱,所以CC1⊥平面ABC.又AD⊂平面ABC,所以CC1⊥AD.又因为AD⊥DE,CC1,DE⊂平面BCC1B1,CC1∩DE=E,所以AD⊥平面BCC1B1.又AD⊂平面ADE,所以平面ADE⊥平面BCC1B1.(2)证明 因为A1B1=A1C1,F为B1C1的中点,所以A1F⊥B1C1.因为CC1⊥平面A1B1C1,且A1F⊂平面A1B1C1,所以CC1⊥A1F.又因为CC1,B1C1⊂平面BCC1B1,CC1∩B1C1=C1,所以A1F⊥平面BCC1B1.由(1)知AD⊥平面BCC1B1,所以A1F∥AD.又AD⊂平面ADE,A1F⊄平面ADE,所以A1F∥平面ADE.名师点析(1)空间中的平行关系有三种:线线平行、线面平行、面面平行.①证明线线平行的常用方法有7种:a.利用两直线平行的定义;b.利用平行线的传递性;c.利用三角形中位线定理;d.利用平行四边形对边平行;e.利用线面平行的性质定理;f.利用线面垂直的性质定理;g.利用面面平行的性质定理.②证明线面平行的常用方法有3种:a.利用线面平行的定义;b.利用线面平行的判定定理;c.利用面面平行的性质.③证明面面平行的常用方法有3种:a.利用面面平行的定义;b.利用面面平行的判定定理;c.利用面面平行的结论:垂直于同一直线的两个平面平行.(2)空间中的垂直关系有三种:线线垂直、线面垂直、面面垂直.①证明线线垂直的常用方法有4种:a.利用两直线垂直的定义;b.利用线面垂直的定义;c.利用勾股定理;d.利用等腰三角形三线合一.②证明线面垂直的常用方法有3种:a.利用线面垂直的定义;b.利用线面垂直的判定定理;c.利用面面垂直的性质.③证明面面垂直的常用方法有2种:a.面面垂直的定义;b.利用面面垂直的判定定理.变式训练3如图,AB是圆O的直径,PA垂直圆O所在的平面,C是圆O上的点.(1)求证:BC⊥平面PAC;(2)设Q为PA的中点,G为△AOC的重心,求证:QG∥平面PBC.证明 (1)由AB是圆O的直径,得AC⊥BC.由PA⊥平面ABC,BC⊂平面ABC,得PA⊥BC.又PA∩AC=A,PA⊂平面PAC,AC⊂平面PAC,所以BC⊥平面PAC.(2)如图,连接OG并延长交AC于点M,连接QM,QO,由G为△AOC的重心,得M为AC的中点.由Q为PA的中点,得QM∥PC,又O为AB的中点,得OM∥BC.因为QM∩MO=M,QM⊂平面QMO,MO⊂平面QMO,BC∩PC=C,BC⊂平面PBC,PC⊂平面PBC,所以平面QMO∥平面PBC.因为QG⊂平面QMO,所以QG∥平面PBC.例4如图所示,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD= ,AD=2,PA=PD= ,E,F分别是棱AD,PC的中点.(1)求证:EF∥平面PAB;(2)若二面角P-AD-B的平面角为60°.①求证:平面PBC⊥平面ABCD;②求直线EF与平面PBC所成角的正弦值.(1)证明 如图所示,取PB的中点M,连接MF,AM.因为F为PC的中点,所以MF∥BC,且MF= BC.由已知有BC∥AD,且BC=AD,又由于E为AD的中点,因而MF∥AE,且MF=AE,故四边形AMFE为平行四边形,所以EF∥AM.又AM⊂平面PAB,而EF⊄平面PAB,所以EF∥平面PAB.(2)①证明 连接PE,BE.因为PA=PD,BA=BD,且E为AD的中点,所以PE⊥AD,BE⊥AD,所以∠PEB为二面角P-AD-B的平面角.在△PAD中,由PA=PD= ,AD=2,可解得PE=2.在△ABD中,由BA=BD= ,AD=2,可解得BE=1.在△PEB中,PE=2,BE=1,∠PEB=60°,故可得∠PBE=90°,即BE⊥PB.又BC∥AD,BE⊥AD,从而BE⊥BC,又BC∩PB=B,BC,PB⊂平面PBC,因此BE⊥平面PBC.又BE⊂平面ABCD,所以平面PBC⊥平面ABCD.名师点析(1)求异面直线所成的角常用平移转化法(转化为相交直线的夹角).(2)求直线与平面所成的角常用射影转化法(即作垂线、找射影).(3)二面角的平面角的作法常有三种:①定义法;②垂线法;③垂面法.变式训练4如图,正方体的棱长为1,B'C∩BC'=O.求:(1)AO与A'C'所成角的大小;(2)AO与平面ABCD所成角的正切值;(3)平面AOB与平面AOC所成二面角的大小.解 (1)∵A'C'∥AC,∴AO与A'C'所成的角是∠OAC.∵AB⊥平面BC',OC⊂平面BC',∴OC⊥AB.又OC⊥BO,AB∩BO=B,∴OC⊥平面ABO.又OA⊂平面ABO,∴OC⊥OA.∴∠OAC=30°.即AO与A'C'所成角为30°.(2)如图,过点O作OE⊥BC于点E,连接AE.∵平面BC'⊥平面ABCD,∴OE⊥平面ABCD,∴∠OAE为OA与平面ABCD所成的角.(3)由(1)知OC⊥平面AOB.又OC⊂平面AOC,∴平面AOB⊥平面AOC.即平面AOB与平面AOC所成的二面角为90°.