





- 8.2 立体图形的直观图课件PPT 课件 0 次下载
- 8.4.2 空间点、直线、平面之间的位置关系课件PPT 课件 0 次下载
- 第八章 章末整合课件PPT 课件 0 次下载
- 第九章 章末整合课件PPT 课件 1 次下载
- 10.2 事件的相互独立性课件PPT 课件 1 次下载
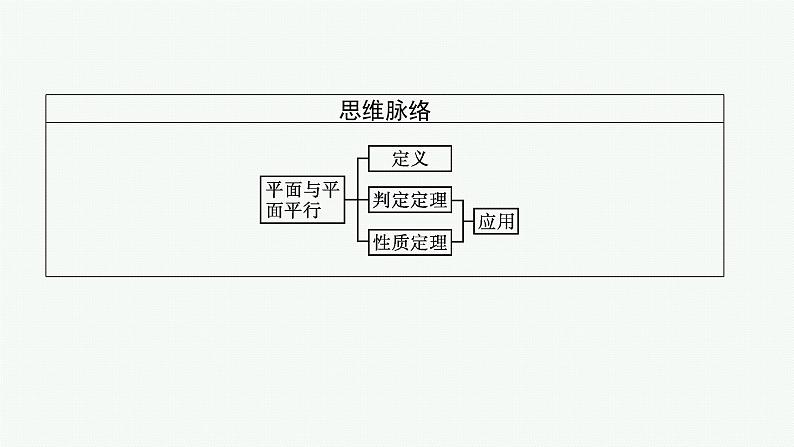
高中数学人教A版 (2019)必修 第二册8.5 空间直线、平面的平行课文内容ppt课件
展开1.理解并掌握平面与平面平行的判定定理.(数学抽象)2.理解并掌握平面与平面平行的性质定理.(数学抽象)3.会证明平面与平面平行的性质定理.(逻辑推理)4.能够应用平面与平面平行的判定定理和性质定理证明相关问题.(直观想象、逻辑推理)
在教室里,天花板所在的平面与地面平行,那么在天花板上任意作一条直线,这条直线与地面是平行的吗?天花板所在的平面与地面都和黑板所在的墙面相交,这两条交线平行吗?
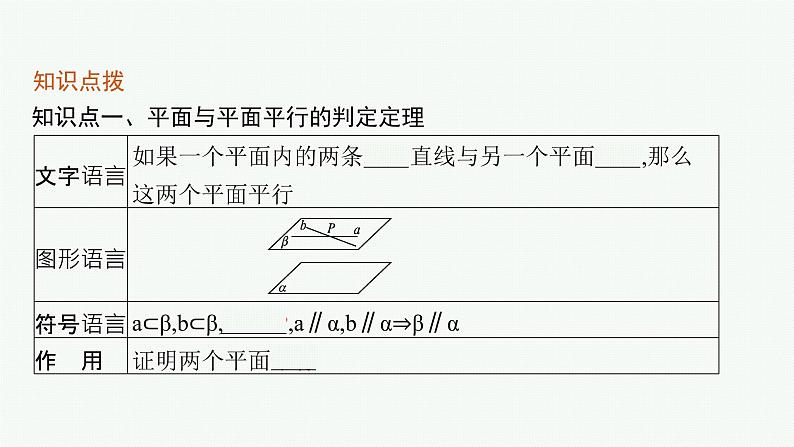
知识点一、平面与平面平行的判定定理
要点笔记(1)定理中,要紧紧抓住“两条”“相交”“平行”这六个字,否则条件不充分,结论不成立.(2)定理体现了化归的数学思想,证明面面平行只需证明两组线面平行.
微练习(1)在长方体ABCD-A'B'C'D'中,下列结论正确的是( )A.平面ABCD∥平面ABB'A'B.平面ABCD∥平面ADD'A'C.平面ABCD∥平面CDD'C'D.平面ABCD∥平面A'B'C'D'(2)判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.①如果一个平面内有两条直线和另一个平面平行,那么这两个平面平行.( )②直线a∥平面β,直线b∥平面β,a⊂平面α,b⊂平面α⇒平面α∥平面β.( )
答案 (1)D (2)①× ②×解析 (1)在长方体ABCD-A'B'C'D'中,上底面ABCD与下底面A'B'C'D'平行.
知识点二、平面与平面平行的性质定理
名师点析(1)定理成立的条件:两平面平行,第三个平面与这两个平面都相交.(2)定理的实质:面面平行⇒线线平行,体现了转化思想与判定定理交替使用,可实现线面、线线、面面平行间的相互转化.(3)面面平行还有如下的性质:两个平面平行,一个平面内的直线平行于另一平面.可作为证明直线与平面平行的依据.
微练习(1)若α∥β,a⊂α,b⊂β,下列几种说法正确的是( )①a与β内无数条直线平行;②a与β内的任何一条直线都不垂直;③a∥β.A.①② B.①③C.②③ D.①②③(2)判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画“×”.①平面α∥平面β,平面α∩平面γ=直线a,平面β∩平面γ=直线b⇒a∥b.( )②平面α∥平面β,直线a⊂α,直线b⊂β⇒a∥b.( )答案 (1)B (2)①√ ②×
例1如图所示,在正方体ABCD-A1B1C1D1中,M,E,F,N分别是A1B1,B1C1,C1D1,D1A1的中点,求证:(1)E,F,B,D四点共面;(2)平面MAN∥平面EFDB.
分析(1)只需证明BD∥EF,即可证明E,F,B,D共面.(2)要证平面MAN∥平面EFDB,只需证MN∥平面EFDB,AM∥平面EFDB.
证明 (1)连接B1D1.∵E,F分别是B1C1和C1D1的中点,∴EF∥B1D1.又BD∥B1D1,∴BD∥EF.∴E,F,B,D四点共面.(2)由题意知MN∥B1D1,B1D1∥BD,∴MN∥BD.又MN⊄平面EFDB,∴MN∥平面EFDB,连接MF.∵点M,F分别是A1B1与C1D1的中点,∴MF?AD.∴四边形ADFM是平行四边形.∴AM∥DF.
∵AM⊄平面EFDB,DF⊂平面EFDB,∴AM∥平面EFDB.又AM∩MN=M,∴平面MAN∥平面EFDB.
反思感悟 证明两个平面平行的方法证明两个平面平行,可以用定义,也可以用判定定理.但用定义证明时,需说明两个平面没有公共点,这一点也不容易做到(可用反证法),所以通常用判定定理证明两个平面平行,其步骤如下:
延伸探究本例中,设P是棱AA1的中点,其他条件不变,求证:平面PMN∥平面C1BD.
证明 连接AB1.∵P,M分别是AA1,A1B1的中点,∴PM∥AB1.又AB1∥C1D,∴PM∥C1D.又PM⊄平面C1BD,C1D⊂平面C1BD,∴PM∥平面C1BD.同理MN∥平面C1BD.又PM∩MN=M,∴平面PMN∥平面C1BD.
例2如图,已知平面α∥平面β,点P是平面α,β外的一点(不在α与β之间),直线PB,PD分别与α,β相交于点A,B和C,D.(1)求证:AC∥BD;(2)已知PA=4,AB=5,PC=3,求PD的长.
分析(1)由面面平行的性质定理直接推证;(2)先由三角形相似得对应线段成比例,再求值.
(1)证明 ∵PB∩PD=P,∴直线PB和PD确定一个平面γ,则α∩γ=AC,β∩γ=BD.又α∥β,∴AC∥BD.(2)解 由(1)得AC∥BD,
反思感悟 证明线线平行的方法(1)定义法:在同一个平面内没有公共点的两条直线平行.(2)平行线的传递性:平行于同一条直线的两条直线平行.
延伸探究在本例中,若P在α与β之间,在第(2)问条件下求CD的长.
解 如图,∵PB∩PC=P,∴PB,PC确定平面γ,γ∩α=AC,γ∩β=BD.又α∥β,∴AC∥BD,∴△PAC∽△PBD,
例3在底面是平行四边形的四棱锥P-ABCD中,点E在PD上,且PE∶ED=2∶1,M为PE的中点,在棱PC上是否存在一点F,使平面BFM∥平面AEC?并证明你的结论.
解 当F是棱PC的中点时,平面BFM∥平面AEC.证明如下,取PC的中点F,连接BF,BM,MF.∵M是PE的中点,∴FM∥CE.∵FM⊄平面AEC,CE⊂平面AEC,∴FM∥平面AEC.
得E为MD的中点,连接BD,如图所示,设BD∩AC=O,则O为BD的中点.
连接OE,则BM∥OE.∵BM⊄平面AEC,OE⊂平面AEC,∴BM∥平面AEC.∵FM⊂平面BFM,BM⊂平面BFM,FM∩BM=M,∴平面BFM∥平面AEC.
反思感悟 探索型问题的类型及解法探索型问题是具有开放性和发散性的问题,此类题目的条件或结论不完备,需要自己去探索,结合已有条件,进行观察、分析、比较和概括得出结论.常见的有以下两类:条件探索型和结论探索型.条件探索型问题是针对一个结论,条件未知需探索;结论探索型是先探索结论再去证明,在探索过程中常先从特殊情况入手,通过观察、分析、归纳,进行猜测,得出结论,再就一般情况去论证结论.
变式训练如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别是棱CC1,C1D1,D1D,CD的中点,N是BC的中点,点M在四边形EFGH的边及其内部运动,当点M在 时,有MN∥平面B1BDD1.
答案 点F,H的连线上
解析 点M在F,H的连线上时,有MN∥平面B1BDD1.如图,平面BDD1B1是正方体ABCD-A1B1C1D1的对角面,探究过点N且与平面BDD1B1平行的直线,可取B1C1的中点N1,连接N1N,则NN1∥平面BDD1B1,连接NH,则NH∥平面BDD1B1.∵NH∩NN1=N,∴平面NN1FH∥平面BDD1B1.∵MN⊂平面NN1FH,∴MN∥平面B1BDD1.即点M在点F,H的连线上时,有MN∥平面B1BDD1.
转化与化归思想在线面、面面平行性质定理中的应用典例已知有公共边AB的两个全等的矩形ABCD和ABEF不在同一个平面内,P,Q分别是对角线AE,BD的中点.求证:PQ∥平面CBE.
证明 (方法一)如图①,取AB的中点G,连接PG和GQ.因为P是AE的中点,所以PG∥EB.又PG⊄平面CBE,EB⊂平面CBE,所以PG∥平面CBE.同理可证GQ∥平面CBE.又PG∩GQ=G,PG⊂平面PGQ,GQ⊂平面PGQ,所以平面PGQ∥平面CBE.因为PQ⊂平面PGQ,PQ⊄平面CBE,所以PQ∥平面CBE.
(方法二)如图②,连接AC,则Q∈AC,且Q是AC的中点.因为P是AE的中点,所以PQ∥EC.因为PQ⊄平面CBE,EC⊂平面CBE,所以PQ∥平面CBE.
方法点睛 (1)线线、线面、面面间的平行关系的判定和性质,常常是通过线线关系、线面关系、面面关系的相互转化来表达的,因此在证明有关问题时,应抓住“转化”这种思想方法来达到论证的目的.(2)空间中线线、线面、面面平行关系的转化如下:
1.(2021山西高一期末)对于两个不同的平面α,β和三条不同的直线a,b,c.有以下几个命题:①若a∥b,b∥c,则a∥c;②若a∥α,b∥α,则a∥b;③若a∥b,b∥α,则a∥α;④若a∥α,a∥β,则α∥β;⑤若a∥α,α∥β,则a∥β.则其中所有错误的命题是( )A.③④⑤B.②④⑤C.②③④D.②③④⑤
答案 D解析 因为a∥b,b∥c,根据空间中直线平行的传递性,得a∥c,故①正确;因为a∥α,b∥α,所以直线a,b平行、异面、相交均有可能,故②错误;若a∥b,b∥α,则a∥α或a⊂α,故③错误;若a∥α,a∥β,则平面α,β平行或相交,故④错误;若a∥α,α∥β,则a∥β或a⊂β,故⑤错误.所以错误的命题是②③④⑤.故选D.
2.若P,Q,R分别是三棱锥S-ABC三条侧棱SA,SB,SC的中点,则平面ABC与平面PQR的位置关系是( )A.平行B.相交C.重合D.相交或平行答案 A解析 由三角形中位线的性质知PQ∥AB,PR∥AC,由线面平行的判定定理,可得PQ∥平面ABC,PR∥平面ABC,又PQ∩PR=P,根据面面平行的判定定理,可得平面ABC∥平面PQR.
3.(多选题)以下说法中,正确的有( )A.在平面α内有两条直线和平面β平行,那么这两个平面平行B.在平面α内有无数条直线和平面β平行,那么这两个平面平行C.平面α内△ABC的三个顶点在平面β的同一侧且到平面β的距离相等且不为0,那么这两个平面平行D.平面α内有无数个点到平面β的距离相等且不为0,那么这两个平面平行或相交
解析 如图①,在平面α内作α,β交线的无数条平行线,可知A,B错误;对C,由题意可知AB∥β,BC∥β,AB∩BC=B,由面面平行的判定定理可知α∥β,C正确;对D,参考选项C的解析,假设α内有一个点位于点A处,而其余点均位于直线BC上,则两个平面平行;如图②,α内有一个点位于点A处,而其余点均位于直线BC上,点A,B,C到平面β的距离相等且不为0,可知两个平面相交,D正确.故选CD.
4.已知直线a∥平面α,平面α∥平面β,则a与β的位置关系为 . 答案 a⊂β或a∥β解析 若a⊂β,则显然满足题目条件.若a⊄β,过直线a作平面γ,γ∩α=b,γ∩β=c,于是由直线a∥平面α得a∥b,由α∥β得b∥c,所以a∥c,又a⊄β,c⊂β,所以a∥β.
人教A版 (2019)必修 第二册第八章 立体几何初步8.5 空间直线、平面的平行说课ppt课件: 这是一份人教A版 (2019)必修 第二册第八章 立体几何初步8.5 空间直线、平面的平行说课ppt课件,共33页。PPT课件主要包含了证线面平行,证面面平行,证无限,证有限,不一定,𝒂与𝜷不一定平行,平面𝒂平面𝜷,图形语言,生活应用,符号语言等内容,欢迎下载使用。
数学人教A版 (2019)8.5 空间直线、平面的平行优秀ppt课件: 这是一份数学人教A版 (2019)8.5 空间直线、平面的平行优秀ppt课件,共28页。PPT课件主要包含了学习目标,新知学习,易错辨析,典例剖析,随堂小测,课堂小结等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第二册第八章 立体几何初步8.5 空间直线、平面的平行说课ppt课件: 这是一份高中数学人教A版 (2019)必修 第二册第八章 立体几何初步8.5 空间直线、平面的平行说课ppt课件,共32页。













