初中数学沪科版八年级上册12.3 一次函数与二元一次方程教学演示课件ppt

这是一份初中数学沪科版八年级上册12.3 一次函数与二元一次方程教学演示课件ppt，共38页。PPT课件主要包含了知识回顾，从“函数值”的角度看，新课导入，探究新知，x-y3，y2x-3，二元一次方程，一次函数，归纳总结，对应练习等内容，欢迎下载使用。

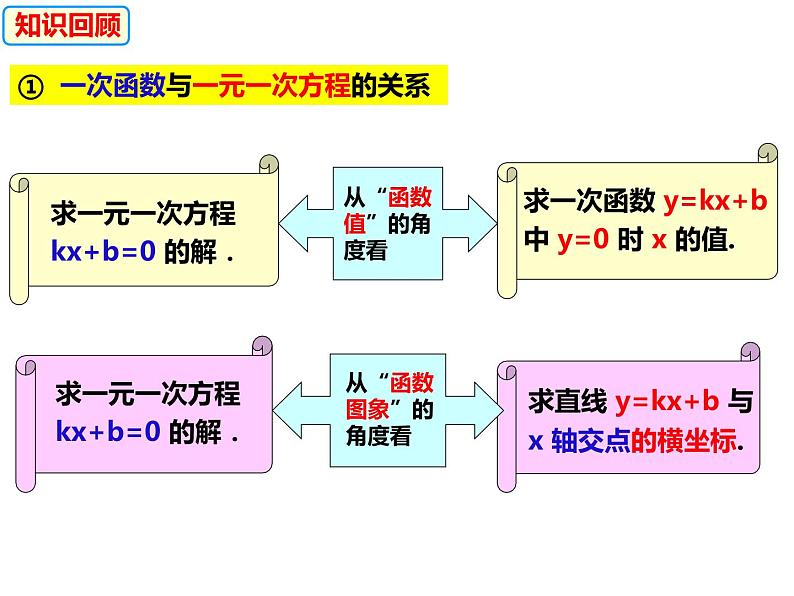
① 一次函数与一元一次方程的关系
求一元一次方程kx+b=0 的解．
求一次函数 y=kx+b 中 y=0 时 x 的值.
从“函数图象”的角度看
求直线 y=kx+b 与 x 轴交点的横坐标.
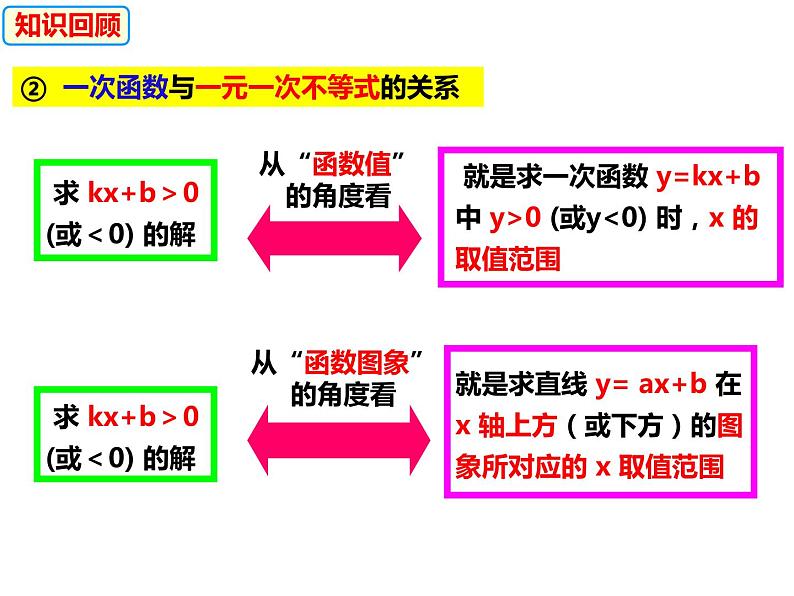
② 一次函数与一元一次不等式的关系
求 kx+b＞0(或＜0) 的解
就是求直线 y= ax+b 在x 轴上方（或下方）的图象所对应的 x 取值范围
就是求一次函数 y=kx+b中 y>0 (或y<0) 时，x 的取值范围
虽然利用函数图象解方程和不等式未必简便，
下面，我们来研究一次函数与二元一次方程的联系.
前面，我们共同学习了一次函数与一元一次方程、一元一次不等式的关系.
但是，这种数形结合的思想方法，对于学习数学是极为重要的.
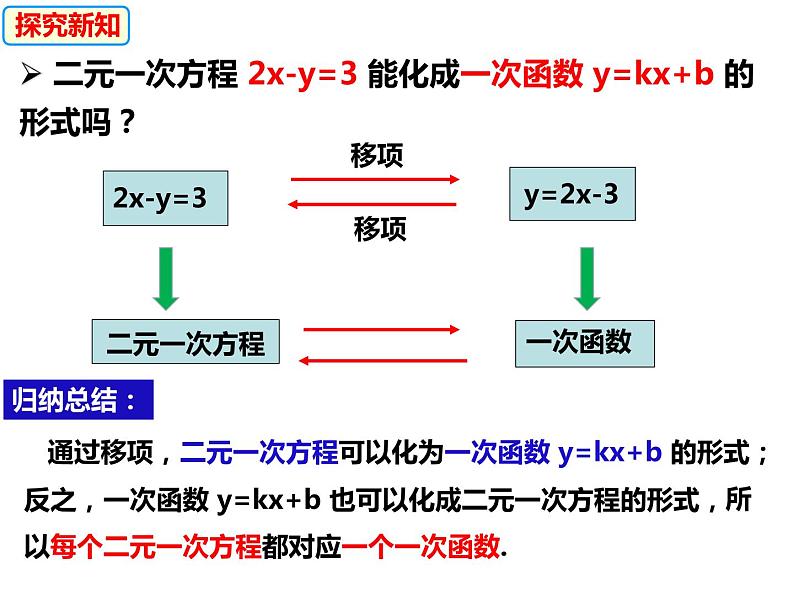
 二元一次方程 2x-y=3 能化成一次函数 y=kx+b 的形式吗？
通过移项，二元一次方程可以化为一次函数 y=kx+b 的形式；反之，一次函数 y=kx+b 也可以化成二元一次方程的形式，
所以每个二元一次方程都对应一个一次函数.
 把下列二元一次方程写成 y=kx＋b 的形式：
(1) 2x-y =0
(2) x+ y=6
y =- x+18
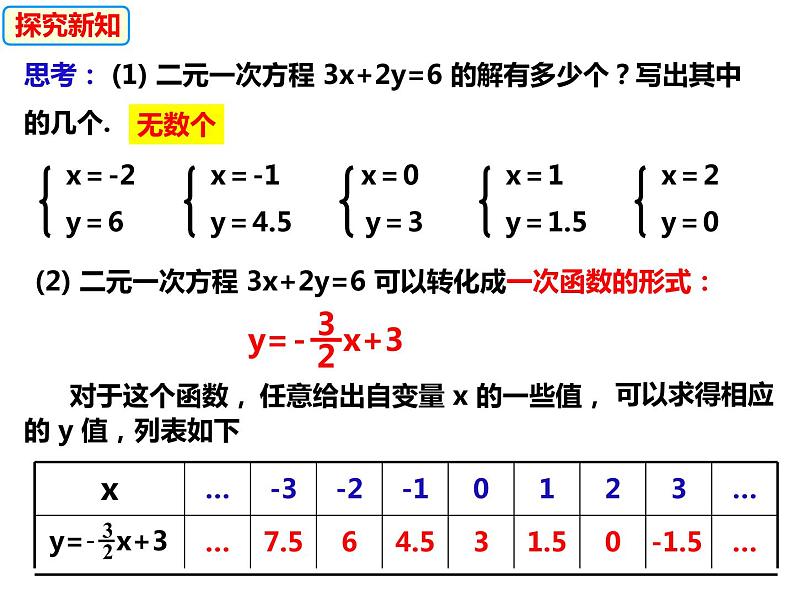
思考： (1) 二元一次方程 3x+2y=6 的解有多少个？写出其中的几个.
(2) 二元一次方程 3x+2y=6 可以转化成一次函数的形式：
可以求得相应的 y 值，列表如下
任意给出自变量 x 的一些值，
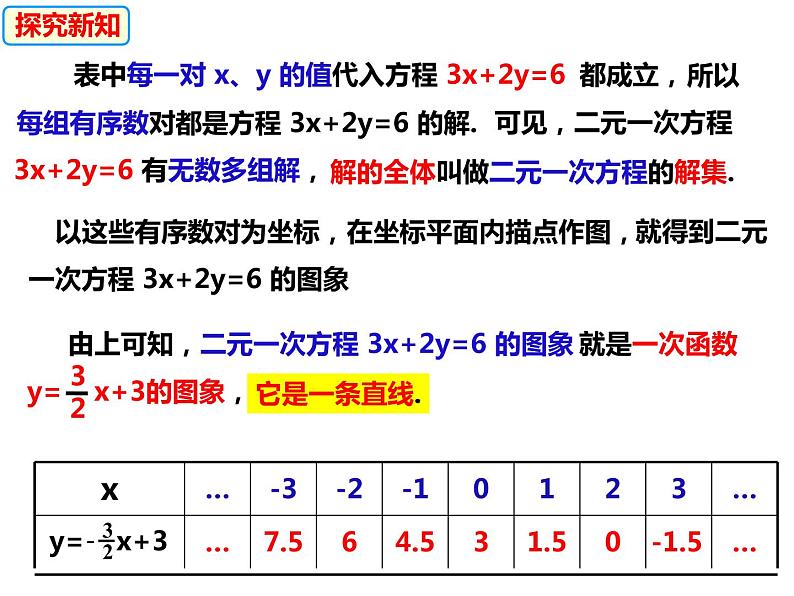
就是一次函数 y= x+3的图象，
表中每一对 x、y 的值代入方程 3x+2y=6
可见，二元一次方程3x+2y=6 有无数多组解，
解的全体叫做二元一次方程的解集.
以这些有序数对为坐标，
在坐标平面内描点作图，
就得到二元一次方程 3x+2y=6 的图象
由上可知，二元一次方程 3x+2y=6 的图象
所以每组有序数对都是方程 3x+2y=6 的解.
一般地，任何一个二元一次方程可以转化成一次函数 y=kx+b(k，b为常数，且k≠0) 的形式，所以每个二元一次方程都对应一个一次函数，
都在一次函数 y=kx+b 的图象上.
思考：二元一次方程 kx-y+b=0 的解与相应的一次函数 y=kx+b 图象上的点有什么关系？你认为应如何表述?
一般地，一次函数 y=kx+b 的图象上任意一点的坐标
以二元一次方程 kx-y+b=0 的解
都是二元一次方程 kx-y+b=0 的一个解;
一次函数y=kx+b(k≠0)
相应的二元一次方程
一次函数y=kx+b(k≠0)图像上点的坐标
相应的二元一次方程的解
一次函数与二元一次方程的关系
1、在平面直角坐标系中画出下列二元一次方程所对应的直线：
2、下面有序数对，哪个是二元一次方程 3x+y=6 的解？ A(2,0)、B(3,－3)、C(5,-9)、 D(6,-10)、E(-2,10)、F(-3,15)
点A、点B、点C、点F
3、二元一次方程 2x+y=3 的解有 个，以这些解为坐标的点，都在一次函数 的图象上.
4、直线上每个点的坐标都是二元一次方程 x－2y＝2 的解直线是( )
5、已知二元一次方程 3x-y=1 的一个解是 ，那么点 P(a,b) 一定不在( )
前面我们学习了一次函数与二元一次方程间的对应关系，
那么我们是否可以利用一次函数来解二元一次方程组呢？
交点P的坐标是二元一次方程组的解.
2x-y=-6
上任意一点的坐标
所以直线 l1与 l2的交点P的坐标
方程x+2y=2可以转化成一次函数 ，
例 1 (1) 在同一个直角坐标系中，画出直线 l1：y=- x+1 与 直线 l2：y=2x+6 的图像;
一次函数与二元一次方程组的关系
(2) 如果直线 l1 与 l2 相交于点P，写出点 P 的坐标 P( , );
(3) 检验点 P 的坐标是不是下面方程组的解？
因此，直线 l1：
直线 l2：y=2x+6
都是方程2x-y=-6的解.
都是方程x+2y=2的解;
就是相应的两条直线的交点坐标.
两个一次函数的交点坐标就
是相应的二元一次方程组的解;
关于 x , y 的二元一次方程组
就是两直线y=k1x+b1 与y=k2x+b2的交点坐标；
求直线 l1：y=k1x+b1 与直线 l2：y=k2x+b2的交点坐标，
就是解关于 x , y 的二元一次方程组
两条直线的交点坐标为 ，
例 2 利用函数图象解方程组
方程 2x-y=2 可化为
方程 x+y=-5 可化为
画出直线y=2x-2和直线y=-x-5的图象
这样用作图的方法求解二元一次方程组的方法，叫做二元一次方程组的图象法，由此我们发现数和形有着密不可分的联系.
你能归纳运用图象法解二元一次方程组的一般步骤吗？
通过以上探讨我们知道，用图象法解二元一次方程组时，应先在同一平面直角坐标系内画出这两个二元一次方程的图象，这两条直线若相交，其交点的坐标，就是方程组的解.
两条直线重合，
1、 利用函数图象解方程组
方程 5x-2y=4 可化为
方程 10x-4y=8 可化为
画出直线y= x-2和直线y= x-2的图象
所以原方程组有无数组解
所以直线上的每一点的坐标都是原方程组的解.
2、 利用函数图象解方程组
方程 3x+2y=-2 可化为
方程 6x+4y=4 可化为
画出直线y=- x-1和直线y=- x+1的图象
所以原方程组无解.
y=- x-1
y=- x+1
 两直线交点个数与二元一次方程组解得个数关系：
思考： 通过以上学习你能发现二元一次方程组的解有几种情况？
上述例题直观地说明了二元一次方程组的解有三种情况.
当把其中的各个二元一次方程组化为标准形式: 后,
从中你发现了怎样的规律？
两个方程中x的系数之比、
以及常数项之比，
对应的两直线的位置关系
二元一次方程组的解的情况
但常数项之比不相等时，
① 如果x的系数之比与y的系数之比不相等，
② 如果x的系数之比、y的系数之比、常数项之比都相等，
③ 如果x的系数之比与y的系数之比相等，
则两直线有一个交点，方程组有一组解.
则两直线重合，方程组有无数组解.
则两直线平行，方程组无解.
1、既不解方程也不画图，你能判断下列方程组的解的情况吗？
3、若二元一次方程组 的解为 ,则函数 与 y=2x-2 的图象的交点坐标为 .
2、一次函数y=5-x与y=2x-1图象的交点为(2,3)， 则方程组 的解为 .
4、如下图，直线 l1 对应的函数表达式为 y=-3x+3，且 l1 与 x轴交于点 D，直线 l2 经过 A，B 两点，直线 l1， l2 相交于点 C.
(1) 求点 D 的坐标；
(2) 求直线 l2 对应的函数表达式；
(3) 求三角形 ADC 的面积.
(4) 在直线 l2 上存在异于点 C 的另一点 P，使得三角形 ADP 与三角形 ADC 的面积相等，请直接写出点 P 的坐标.
5、如图，已知直线 l1：y1=-2x-3，直线 l2 ：y2= x+3，l1 与 l2 相交于点 P，l1，l2 分别与 y 轴相交于点 A，B． (1) 求点 P 的坐标． (2) 若 y1＞y2＞0，求 x 的取值范围． (3) 点 D (m，0) 为 x 轴上的一个动点，过点 D 作 x 轴的垂线分别交 l1 和 l2 于点 E，F，当 EF=3 时，求 m 的值．
① 一次函数与二元一次方程的关系
② 一次函数与二元一次方程组的关系
③ 运用图象法解二元一次方程组的一般步骤：
1、在平面直角坐标系 xOy 中，一次函数 y=kx+b(k≠0) 的图象由函数 y=x 的图象平移得到，且经过点 (1，2). (1) 求这个一次函数的解析式； (2) 当 x＞1 时，对于 x 的每一个值，函数 y=mx (m≠0) 的值 大于一次函数 y=kx+b 的值，直接写出 m 的取值范围.