




高中5.1 任意角和弧度制教学演示课件ppt
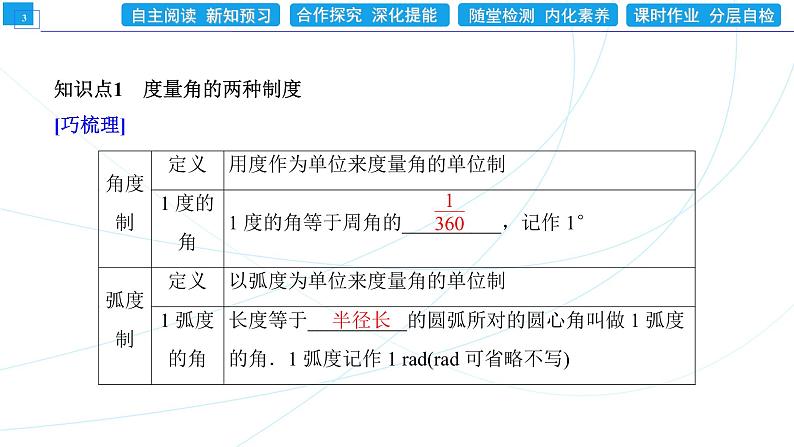
展开知识点1 度量角的两种制度[巧梳理]
[微点拨](1)用弧度为单位表示角的大小时,“弧度”或“rad”可以略去不写,只写这个角对应的弧度数即可.(2)不管是以弧度还是以度为单位度量角的大小,都是一个与半径大小无关的定值.
[微体验]1.下列说法中正确的是( )A.1弧度是1度的圆心角所对的弧B.1弧度是长度为半径长的弧C.1弧度是1度的弧与1度的角之和D.1弧度是长度等于半径长的弧所对的圆心角的大小,它是角的一种度量单位
解析:D 利用弧度的定义及角度的定义判断.
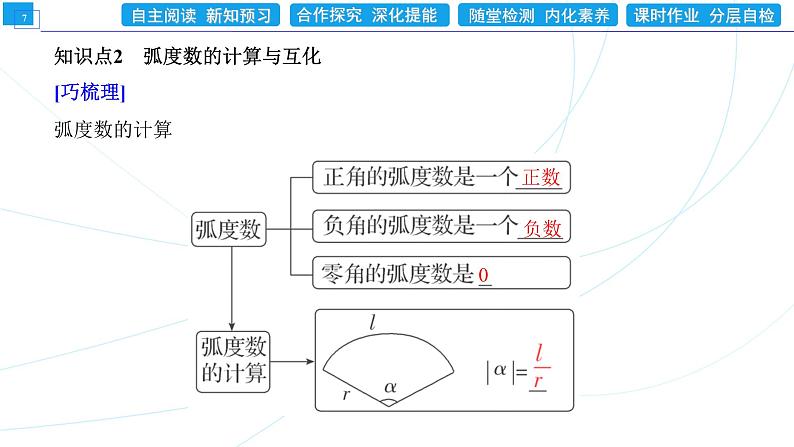
知识点2 弧度数的计算与互化[巧梳理]弧度数的计算
知识点3 弧度制下扇形的弧长与面积公式(R是扇形所在圆的半径,n°为扇形的圆心角)[巧梳理]
[微点拨]在应用弧度制下的弧长公式、扇形面积公式时,要注意α的单位是“弧度”,而不是“度”,若已知角是以“度”为单位的,则应先化成“弧度”,再代入计算.
[微体验]3.弧长为3π,圆心角为135°的扇形的半径为__________,面积为__________.答案:4 6π
学习任务一 角度与弧度的换算[例1] (链接教材P173例4)将下列角度与弧度进行互化:
角度制与弧度制的互化原则和方法[注意] 用“弧度”为单位度量角时,常常把弧度数写成多少π的形式,如无特别要求,不必把π写成小数.
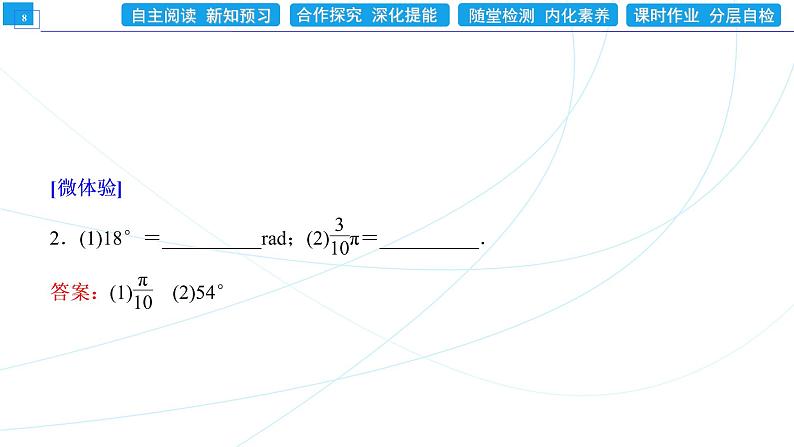
2.把下列角度化为弧度:(1)-1500°=__________;(2)67°30′=__________.
学习任务二 用弧度制表示角的集合[例2] (链接教材P175T3)把下列角化成2kπ+α(0≤α<2π,k∈Z)的形式,指出它是第几象限角并写出与α终边相同的角的集合.
弧度制下与角α终边相同的角的表示在弧度制下,与角α的终边相同的角可以表示为{β|β=2kπ+α,k∈Z},即与角α终边相同的角可以表示成α加上2π的整数倍.[注意] (1)注意角度与弧度不能混用;(2)各终边相同的角需加2kπ,k∈Z.
学习任务三 扇形的弧长公式及面积公式的应用[例3] (链接教材P174例6)若扇形的面积是4 cm2,它的周长是10 cm,则扇形圆心角(正角)的弧度数为( )
关于弧度制下扇形问题的解决方法(2)弧长、面积的最值:利用圆心角的弧度数、半径表示出弧长(面积),利用函数知识求最值,一般利用二次函数的最值求解.
[跟踪训练]4.已知一扇形的周长为40 cm,当它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?
4.用弧度制表示终边落在x轴上方的角α的集合为__________.解析:若角α的终边落在x轴上方,则2kπ<α<2kπ+π(k∈Z).答案:{α|2kπ<α<2kπ+π,k∈Z}
基础巩固练1.(多选)下列转化结果正确的是( )
2.用弧度制表示与150°角终边相同的角的集合为( )
7.在扇形中,已知半径为8,弧长为12,则圆心角α是__________ rad,扇形面积S=__________.
8.若圆的半径变为原来的3倍,而所对弧长不变,则该弧所对圆心角是原来圆弧所对圆心角的__________.
综合应用练10.(多选)已知扇形周长为6 cm,面积为2 cm2,则其圆心角的弧度数可能是( )A.1 B.2C.4 D.5
12.已知圆的一段弧长等于该圆外切正三角形的边长,则这段弧所对圆心角的弧度数的绝对值为__________;若圆弧长等于其所在圆的内接正方形的周长,那么这段弧所对圆心角的弧度数的绝对值为__________.
高中数学人教A版 (2019)必修 第一册5.1 任意角和弧度制教课课件ppt: 这是一份高中数学人教A版 (2019)必修 第一册5.1 任意角和弧度制教课课件ppt,共44页。PPT课件主要包含了目标认知,半径长,rad,图5-1-4,一一对应,弧度数,α·r,ABC,图5-1-5,角度一弧长公式等内容,欢迎下载使用。
高中数学人教A版 (2019)必修 第一册第五章 三角函数5.1 任意角和弧度制课文配套ppt课件: 这是一份高中数学人教A版 (2019)必修 第一册第五章 三角函数5.1 任意角和弧度制课文配套ppt课件,共35页。PPT课件主要包含了度量角的两种制度,半径长,角的单位制,rad,πrad,扇形的弧长及面积公式,l=αR等内容,欢迎下载使用。
人教A版 (2019)5.1 任意角和弧度制图片ppt课件: 这是一份人教A版 (2019)5.1 任意角和弧度制图片ppt课件,共29页。PPT课件主要包含了新知初探·课前预习,题型探究·课堂解透,半径长,πrad,答案A,答案C,答案B等内容,欢迎下载使用。













