3.1.2 函数的表示 -【基础过关系列】2022-2023学年高一数学上学期同步知识点剖析精品讲义(人教A版2019必修第一册)

函数的表示

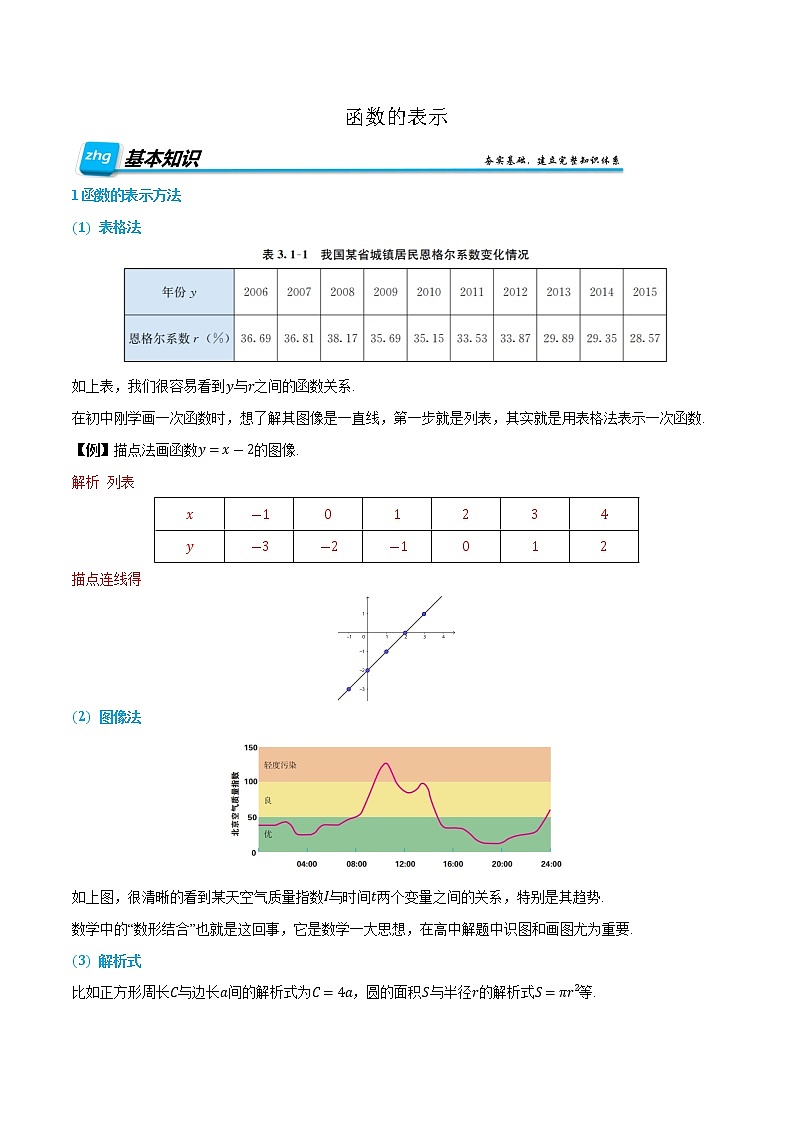
1函数的表示方法

表格法

如上表，我们很容易看到与之间的函数关系.

在初中刚学画一次函数时，想了解其图像是一直线，第一步就是列表，其实就是用表格法表示一次函数.

【例】描点法画函数的图像.

图像法

如上图，很清晰的看到某天空气质量指数与时间两个变量之间的关系，特别是其趋势.

数学中的“数形结合”也就是这回事，它是数学一大思想，在高中解题中识图和画图尤为重要.

解析式

比如正方形周长与边长间的解析式为，圆的面积与半径的解析式等.

求函数解析式的方法

①     配凑法   ② 待定系数法    ③ 换元法    ④ 构造方程组法   ⑤ 代入法

【例】购买某种饮料听，所需钱数是元．若每听元，试分别用解析法、列表法、图象法将表示成的函数．

2 分段函数

定义：有些函数在其定义域中，对于自变量的不同取值范围，对应关系不同，这样的函数通常称为分段函数．

Eg ，.

【例】湛江市自来水公司鼓励企业节约用水，按下表规定收取水费，

 求用水量与水费之间的函数关系，并求用水吨和吨的水费.

【题型1】求函数解析式

方法1 待定系数法

【典题1】 已知函数是二次函数，若，求的解析式．

方法2 换元法

【典题1】 已知，求.

方法3 方程组法

【典题1】 已知，则的解析式是　   　．

【巩固练习】

1. 已知，则有(　　)

A． B． 

C． D．

2.已知，则的解集为      .

3.设是一次函数，且，求的解析式.

4.满足，求的解析式.

【题型2】与分段函数有关问题

【典题1】 已知函数．

(1)画出函数图象；(2)求，的值；(3)当时，求的取值范围．

【典题2】 已知函数与轴有个交点，则实数的取值范围是　       ．

【巩固练习】

1.设函数，若，则实数的值为　   　．

2.已知函数，则不等式的解集为　     ．

3.作下列各函数的图象．

(1)       (2)；   

4. 求函数的值域.

5.已知函数，若互不相等的实数满足，求的取值范围.

【题型3】函数的简单应用

【典题1】 如图所示的四个容器高度都相同，将水从容器顶部一个孔中以相同的速度注入其中，注满为止．用下面对应的图象显示该容器中水面的高度h和时间t之间的关系，其中不正确的有(　　)

A．1个　　      　B．2个　        　　C．3个　　       　D．4个

【典题2】 某产品生产厂家生产一种产品，每生产这种产品(百台)，其总成本为(万元)，其中固定成本为万元，且每生产百台的生产成本为万元(总成本固定成本生产成本)．销售收入(万元)满足假定该产品产销平衡(即生产的产品都能卖掉)，根据上述规律，完成下列问题：

(1)写出利润函数的解析式(利润销售收入总成本)；

(2)要使工厂有盈利，求产量的范围；

(3)工厂生产多少台产品时，可使盈利最大？

【巩固练习】

1.某人去上班，先快速走，后中速走．如果表示该人离单位的距离，表示出发后的时间，那么下列图象中符合此人走法的是　　

2.如图，将水注入下面四种容器中，注满为止．如果注水量与水深的函数关系的图象如图所示，那么容器的形状是　　

3.如图，已知底角为角的等腰梯形，底边长为，腰长为，当一条垂直于底边(垂足为的直线把梯形分成两部分，令，求左边部分的面积关于的函数解析式，并画出图象．