高中数学7.3 三角函数的图象和性质第1课时导学案

这是一份高中数学7.3 三角函数的图象和性质第1课时导学案，共12页。学案主要包含了正弦函数，“五点法”画函数的图象等内容，欢迎下载使用。
学习目标 1.了解正弦函数、余弦函数的图象.2.会用五点法画正弦函数、余弦函数的图象.3.能利用正弦函数、余弦函数的图象解决简单问题．
导语
网上百度一下一个物理实验：“沙摆实验”，就是将一个装满细砂的漏斗挂在一个铁架上做单摆运动时，沙子落在与单摆运动方向垂直的木板上，我们通过实验看看落在木板上的细砂轨迹是什么？
这个轨迹与我们今天要学习的正弦函数、余弦函数的图象有关．
一、正弦函数、余弦函数图象的初步认识
问题1 结合之前所学，研究函数的一般步骤是什么？
提示 先确定函数的定义域，然后画出函数图象，通过图象研究函数的值域、单调性、最值、对称性、奇偶性等函数的性质．
问题2 绘制函数图象，首先要准确绘制其上一点，对于正弦函数，在[0,2π]上任取一个值x0，如何借助单位圆确定正弦函数值sin x0，并画出点T(x0，sin x0)?
提示 如图，在x轴上任取一点O′，以O′为圆心，单位长为半径作圆．在⊙O′中，设的长为x0(即∠AO′P＝x0)，则MP＝sin x0，所以点S(x0，sin x0)是以的长为横坐标，正弦线MP的数量为纵坐标的点．
问题3 我们已经学会绘制函数图象上的点，接下来，如何画函数y＝sin x，x∈[0,2π]的图象？
提示 在⊙O′中，作出对应于eq \f(π,6)，eq \f(π,3)，eq \f(π,2)，…，eq \f(11π,6)的角及相应的正弦线，相应地，把x轴上从0到2π这一段分成12等份．把角x的正弦线向右平移，使它的起点与x轴上表示数x的点重合，再用光滑曲线把这些正弦线的终点连接起来，就得到正弦函数y＝sin x在[0,2π]上的图象，如图所示．
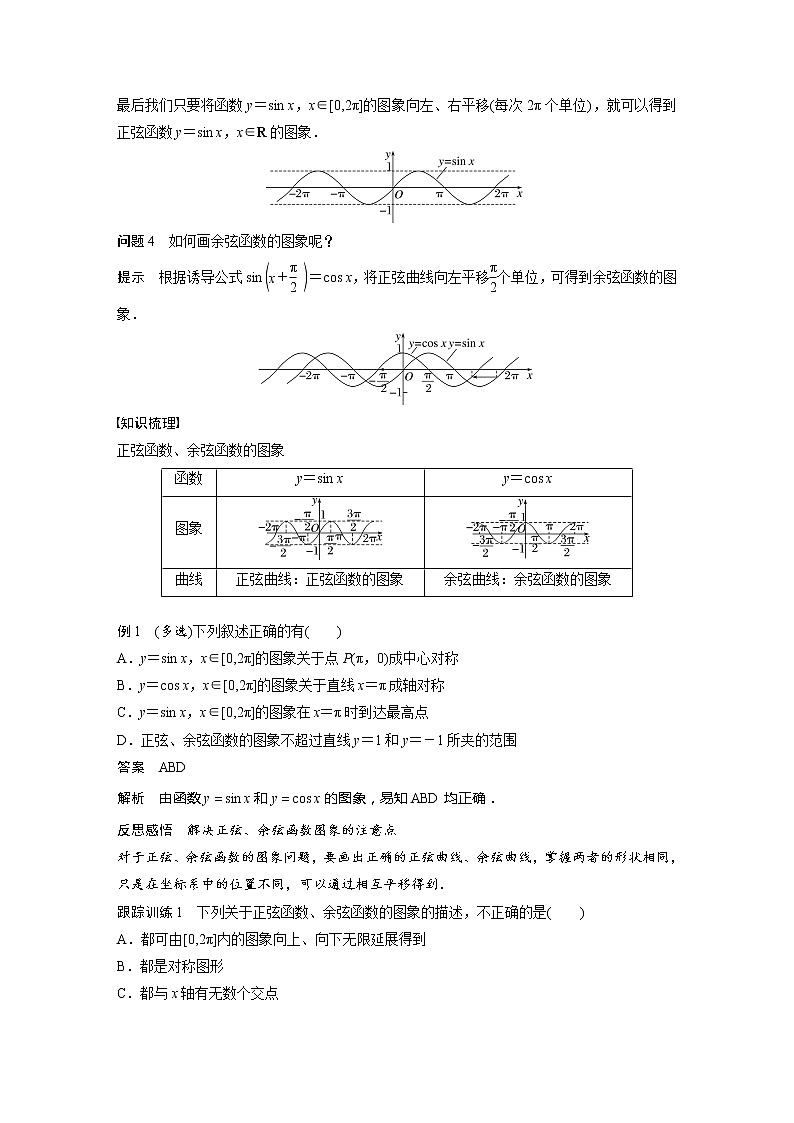
最后我们只要将函数y＝sin x，x∈[0,2π]的图象向左、右平移(每次2π个单位)，就可以得到正弦函数y＝sin x，x∈R的图象．
问题4 如何画余弦函数的图象呢？
提示 根据诱导公式sineq \b\lc\(\rc\)(\a\vs4\al\c1(x＋\f(π,2)))＝cs x，将正弦曲线向左平移eq \f(π,2)个单位，可得到余弦函数的图象．
知识梳理
正弦函数、余弦函数的图象
例1 (多选)下列叙述正确的有( )
A．y＝sin x，x∈[0,2π]的图象关于点P(π，0)成中心对称
B．y＝cs x，x∈[0,2π]的图象关于直线x＝π成轴对称
C．y＝sin x，x∈[0,2π]的图象在x＝π时到达最高点
D．正弦、余弦函数的图象不超过直线y＝1和y＝－1所夹的范围
答案 ABD
解析 由函数y＝sin x和y＝cs x的图象，易知ABD均正确．
反思感悟 解决正弦、余弦函数图象的注意点
对于正弦、余弦函数的图象问题，要画出正确的正弦曲线、余弦曲线，掌握两者的形状相同，只是在坐标系中的位置不同，可以通过相互平移得到．
跟踪训练1 下列关于正弦函数、余弦函数的图象的描述，不正确的是( )
A．都可由[0,2π]内的图象向上、向下无限延展得到
B．都是对称图形
C．都与x轴有无数个交点
D．y＝sin(－x)的图象与y＝sin x的图象关于x轴对称
答案 A
解析 由正弦、余弦函数的图象知，B，C，D正确．
二、“五点法”画函数的图象
知识梳理
“五点法”作图
例2 用“五点法”作出下列函数的简图：
(1)y＝sin x－1，x∈[0,2π]；
(2)y＝－2cs x＋3，x∈[0,2π]．
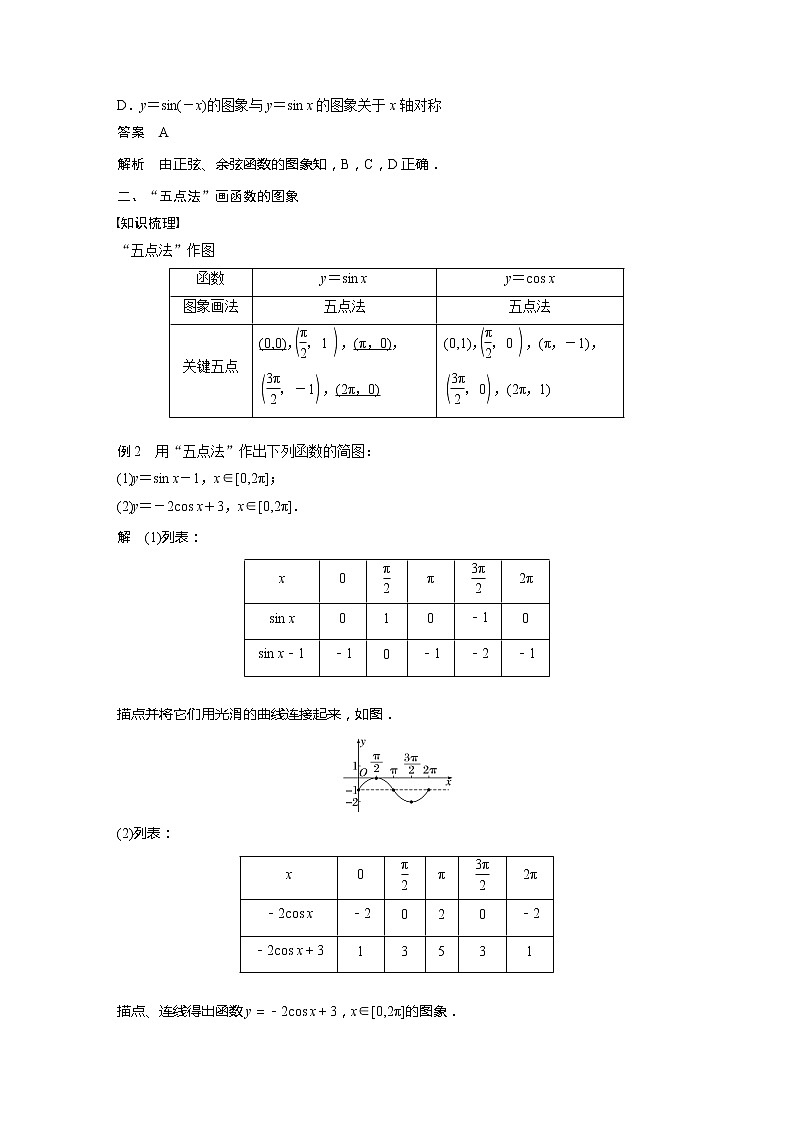
解 (1)列表：
描点并将它们用光滑的曲线连接起来，如图．
(2)列表：
描点、连线得出函数y＝－2cs x＋3，x∈[0,2π]的图象．
反思感悟 作形如y＝asin x＋b(或y＝acs x＋b)，x∈[0,2π]的图象的三个步骤
跟踪训练2 利用“五点法”作出函数y＝2＋cs x(0≤x≤2π)的简图．
解 列表：
描点并将它们用光滑的曲线连接起来，如图．
三、正弦函数、余弦函数图象的应用
例3 方程2sin x－1＝0，x∈[0,2π]的解集为________．
答案 eq \b\lc\{\rc\}(\a\vs4\al\c1(\f(π,6)，\f(5π,6)))
解析 因为2sin x－1＝0，所以sin x＝eq \f(1,2).
在同一直角坐标系下，作函数y＝sin x，x∈[0,2π]以及y＝eq \f(1,2)的图象．又sin eq \f(π,6)＝sin eq \f(5π,6)＝eq \f(1,2).
所以当x∈[0,2π]时，方程2sin x－1＝0的根为eq \f(π,6)和eq \f(5π,6).
延伸探究
1．不等式2sin x－1≥0，x∈[0,2π]的解集为( )
A.eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,6))) B.eq \b\lc\[\rc\](\a\vs4\al\c1(0，\f(π,4)))
C.eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，π)) D.eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(5π,6)))
答案 D
解析 因为2sin x－1≥0，所以sin x≥eq \f(1,2).
在同一直角坐标系下，作函数y＝sin x，x∈[0,2π]以及y＝eq \f(1,2)的图象．又sin eq \f(π,6)＝sin eq \f(5π,6)＝eq \f(1,2).
所以根据图象可知，sin x≥eq \f(1,2)的解集为eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(5π,6))).
2．在本例中把“x∈[0,2π]”改为“x∈R”，求不等式2sin x－1≥0的解集．
解 在x∈[0,2π]上的解集为eq \b\lc\[\rc\](\a\vs4\al\c1(\f(π,6)，\f(5π,6))).
所以x∈R时，不等式的解集为eq \b\lc\{\rc\}(\a\vs4\al\c1(x\b\lc\|\rc\ (\a\vs4\al\c1(\f(π,6)＋2kπ≤x≤\f(5π,6)＋2kπ，k∈Z)))).
反思感悟 利用三角函数图象解三角不等式sin x>a(cs x>a)的步骤
(1)作出相应的正弦函数或余弦函数在[0,2π]上的图象．
(2)确定在[0,2π]上sin x＝a(cs x＝a)的x值．
(3)写出不等式在区间[0,2π]上的解集．
(4)根据公式一写出定义域内的解集．
跟踪训练3 解关于x的不等式eq \f(1,2)