初中数学6 实数备课ppt课件

这是一份初中数学6 实数备课ppt课件，共22页。PPT课件主要包含了学习目标，情境导入，有理数的分类，有限小数，无限循环小数，探索交流，有理数，无理数，有限小数或循环小数，无限不循环小数等内容，欢迎下载使用。

1.了解实数的意义，能对实数按要求分类.(重点）2.了解实数范围内相关概念的意义.(重点）3.了解实数与数轴上点的一一对应关系.能用数轴上的点表示无理数.(难点）
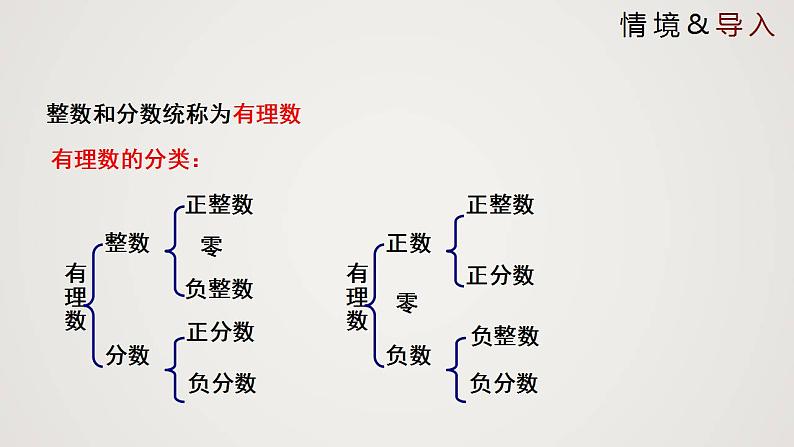
整数和分数统称为有理数
把下列各数写成小数的形式：
有限小数和无限循环小数叫有理数
把下列各数分别填入相应的括号内：
有理数和无理数统称为实数
(1)含π的一些数；(2)含开不尽方的数；(3)有规律但不循环的小数,如1.01001000100001…
例1.下列各数：3.14159，－ ，0.131 131 113…(每相邻两个3之间依次多1个1)，－π， ，－ 中，无理数有(　　) A．1个　 B．2个 　C．3个　 D．4个
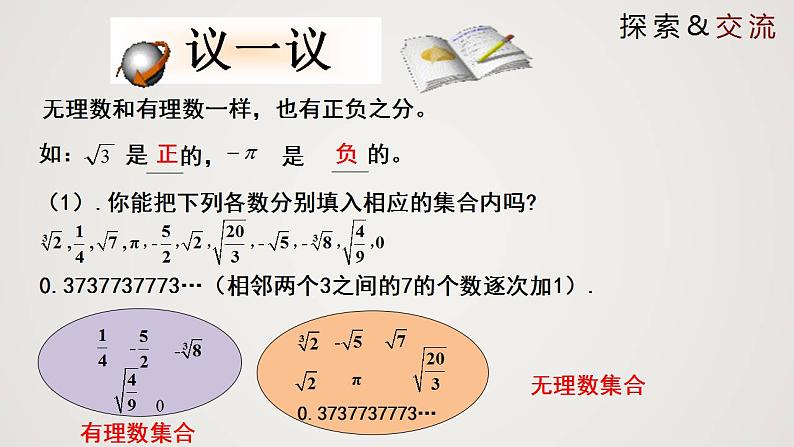
无理数和有理数一样，也有正负之分。
0.3737737773…（相邻两个3之间的7的个数逐次加1）.
0.3737737773…
（1）.你能把下列各数分别填入相应的集合内吗?
（1）0属于正数吗？0属于负数吗？（2）实数除了可以分为有理数与无理数外，实数还可以怎样分类？
例2.下列结论正确的是 （　 　）A. 正数与负数统称为有理数B. 无限小数都是无理数C. 有理数与无理数统称为实数D. 两个无理数的和一定是无理数
在实数范围内，相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.例如： 和 互为相反数， 和 互为倒数，
思考：无理数能进行加、减、乘、除乘法的运算吗？有理数的运算法则和运算律对无理数还适用吗？
实数和有理数一样，能进行加、减、乘、除乘法的运算、有理数的运算法则和运算律对实数仍适用。
例3.若a，b互为相反数，c，d互为倒数，m的绝对值为4，求
解： 因为a，b互为相反数，所以a＋b＝0. 因为c，d互为倒数，所以cd＝1. 因为|m|＝4，所以m＝±4，m2＝16.
（1）a是一个实数，它的相反数为 ，绝对值为 ；
（2）如果a ≠0，那么它的倒数为 .
(1)如图，OA=OB,数轴上点A对应的数是什么？它介于哪两个整数之间？(2)你能在坐标轴上找到 对应的点吗？与同伴进行交流.
A点对应的数等于 ，它介于1与2之间.如果将所有有理数都标到数轴上，数轴未被填满，在数轴上还可以表示无理数.
每一个实数都可以用数轴上的一个点来表示；
反过来，数轴上的每一点都表示一个实数.
实数和数轴上的点是一一对应的.
在数轴上，右边的点比左边的点表示的数大.
例4.点A在数轴上表示的数为 ，点B在数轴上表示的数为－5，则A，B两点之间的距离为 ________．
1.下列说法错误的是 （　　）A.|3-π|= 3-π B. 是无理数C.2的相反数是-2 D. 的倒数是3
2.下列说法：①-5的绝对值是5；②-1的相反数是1；③0的倒数是0；④64的立方根是±4，⑤ 是无理数，⑥4的算术平方根是2，其中正确的有 （　　）2个B. 3个C. 4个D. 5个
3.将下列各数填入相应的集合内。(1)有理数集合：{ …}(2)无理数集合：{ …}(3)负无理数集合：{ …}(4)正实数集合：{ …}
4.计算下列各式的值。