人教版七年级上册3.2 解一元一次方程（一）----合并同类项与移项课文课件ppt

3.2　解一元一次方程(一)——合并同类项与移项

第1课时　利用合并同类项解一元一次方程

【知识梳理】

将方程中的同类项进行      ，把以x为未知数的一元一次方程变形为        (a≠0，a，b为已知数)的形式，然后利用            ，方程两边同时       ，从而得到       .

如：解方程－7x＋2x＝9－4的步骤是：①合并同类项，得         ；②系数化为1，得        .

【习题精选】

一、选择题

1.对于方程8x＋6x－10x＝8,合并同类项正确的是(      )

A.2x＝8  B.3x＝8  C.4x＝8  D.－4x＝8

2.设y1＝3x－2,y2＝2x＋2,且y1＋y2＝10,则x的值为(      )

A.  B.2  C.－2 D.

3.下列是小明同学做的四道解方程题,其中错误的是(      )

A.5x＋4x＝9,得x＝1         B.－2x－3x＝5,得x＝1

C.3x－x＝－1＋3,得x＝1     D.－4x＋6x＝－2－8,得x＝－5

4.如果x＝m是关于x的方程x－m＝1的解，那么m的值是 (　　)

A．0  B．2 C．－2  D．－6

5.若三个连续偶数的和为24,则它们的积为(      )

A.48 B.120 C.240 D.480

6.若＋x＋2x的值是210,则x的值是(      )

A.20 B.40 C.60 D.80

7.挖一条1 210 m的水渠，由甲、乙两队从两头同时施工，甲队每天挖130 m，乙队每天挖90 m，需几天才能挖好？设需用x天才能挖好，则所列方程中正确的是(　　)

A．130x＋90x＝1 210  B．130＋90x＝1 210

C．130x＋90＝1 210  D．(130－90)x＝1 210

8.某人有连续4天的休假，这4天的日期之和是86，则休假第一天的日期是(　　)

A．20日 B．21日 C．22日 D．23日

9.我国古代名著《九章算术》中有一题“今有凫起南海，七日至北海；雁起北海，九日至南海．今凫雁俱起，问何日相逢？”(凫：野鸭)设野鸭与大雁从南海和北海同时起飞，经过x天相遇，则可列方程为(　　)

A．(9－7)x＝1 B．(9＋7)x＝1 C．x＝1 D．x＝1

10.公元前1700年的古埃及纸草书中,记载着一个数学问题:“它的全部,加上它的七分之一,其和等于19.”此问题中“它”的值为(      )

A.  B. C. D.

11.关于x的方程3－x＝2a与方程x＋3x＝28的解相同，则a的值为(　　)

A．2 B．－2 C．5 D．－5

12.如图是日历表，任意圈出一竖列相邻的三个数，请你用方程的思想来研究，发现这三个数的和不可能是(　　)

A．27 B．36 C．40 D．54

二、填空题

13.解方程6x＋9x－12x＝21＋3,合并同类项可得　　　　,将未知数的系数化为1可得　　　　. 

14.小张有三种邮票共18枚,它们的数量之比为1∶2∶3,则最多的一种邮票有　　枚. 

15.《孙子算经》中有这样一道题,原文如下:

今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽,问城中家几何?

大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家再共取一头,恰好取完,问:城中有多少户人家?设城中有x户人家,则可以列方程为　　　　　　. 

16.若关于x的方程2mx＋3m＝－1与3x＋6x＝－3的解相同,则m的值为　　　　. 

17.某校三年共购买计算机140台,去年购买的数量是前年的2倍,今年购买的数量是去年的2倍,则这个学校前年购买了　　　　台计算机. 

18.已知＝1－;…则方程＋…＋＝2 021的解是　　　　. 

19.方程＋…＋＝2 020的解是　　　　. 

三、解答题

20.解方程:

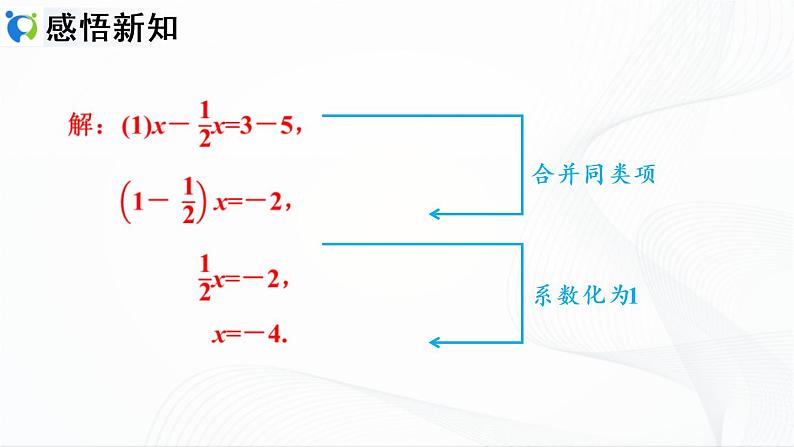
(1)3x＋2x－6x＝－9＋15;

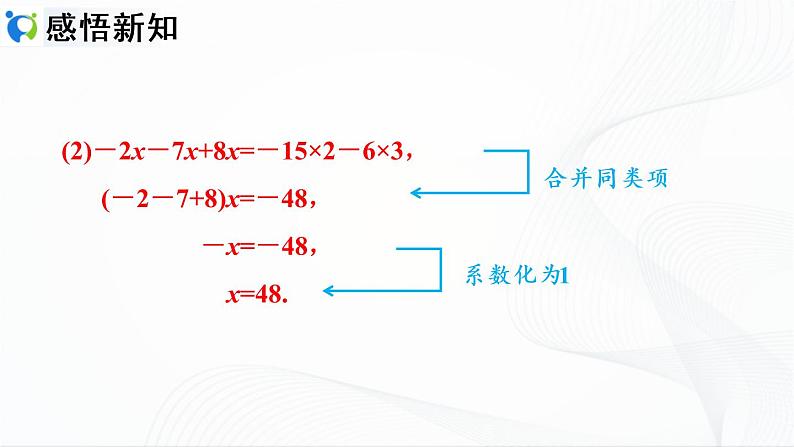
(2)－1.4x＋2.8x＝－7＋9.8;

(3)x－x＋x－x＝.

21.一件夹克衫先按成本价提高60%标价,再将标价打7折出售,结果获利36元,则这件夹克衫的成本价是多少元?

22.用大小两台拖拉机耕地,每小时共耕地30亩.已知大拖拉机的工作效率是小拖拉机的1.5倍,问小拖拉机每小时耕地多少亩?

23.小莹花30元钱买了5千克苹果和2千克香蕉,找回3元.已知每千克香蕉的售价是每千克苹果售价的2倍,则每千克香蕉的售价是多少元?

24.甲、乙两人分别从相距1000米的A,B两地同时出发,相向而行,甲每秒走米,乙每秒走米.甲带一只狗和他同时出发,狗以每秒3米的速度向乙奔去,遇到乙后立即调转头向甲奔去,遇到甲后又调转头向乙奔去,直到甲、乙两人相遇时狗才停下,则这只狗一共跑了多少米?

25.有一列数,按一定规律排列:1,－4,16,－64,256,－1024,…,其中有三个相邻的数的和是－13312,则这三个数分别是多少?

26.【江阴期中】将连续的奇数1，3，5，7…排列成如下的数表，用十字框框出5个数(如下图)．

(1)若将十字框上下左右平移，使得十字框正好框住数列中的5个数．小明发现这五个数的和总等于中间数的整数倍．若设中间的数为a，则框住的5个数字之和为    (用a的代数式表示)；

(2)在(1)的条件下，是否存在a的值，使得该十字框框住的5个数之和恰好等于2 020？若存在，求出此时a的值；若不存在，请说明理由；

(3)在(1)的条件下，十字框框住的5个数之和能等于415吗？若能，分别写出十字框框住的这5个数；若不能，请说明理由．

参考答案

【知识梳理】

将方程中的同类项进行      ，把以x为未知数的一元一次方程变形为        (a≠0，a，b为已知数)的形式，然后利用            ，方程两边同时       ，从而得到       .

如：解方程－7x＋2x＝9－4的步骤是：①合并同类项，得         ；②系数化为1，得        .

【答案】合并  ax＝b   等式的性质2  除以a  x＝   －5x＝5   x＝－1

【习题精选】

一、选择题

1.对于方程8x＋6x－10x＝8,合并同类项正确的是(   C   )

A.2x＝8  B.3x＝8  C.4x＝8  D.－4x＝8

2.设y1＝3x－2,y2＝2x＋2,且y1＋y2＝10,则x的值为(   B   )

A.  B.2  C.－2 D.

3.下列是小明同学做的四道解方程题,其中错误的是(   B   )

A.5x＋4x＝9,得x＝1         B.－2x－3x＝5,得x＝1

C.3x－x＝－1＋3,得x＝1     D.－4x＋6x＝－2－8,得x＝－5

4.如果x＝m是关于x的方程x－m＝1的解，那么m的值是 (　C　)

A．0  B．2 C．－2  D．－6

5.若三个连续偶数的和为24,则它们的积为(   D   )

A.48 B.120 C.240 D.480

6.若＋x＋2x的值是210,则x的值是(   C   )

A.20 B.40 C.60 D.80

7.挖一条1 210 m的水渠，由甲、乙两队从两头同时施工，甲队每天挖130 m，乙队每天挖90 m，需几天才能挖好？设需用x天才能挖好，则所列方程中正确的是(　A　)

A．130x＋90x＝1 210  B．130＋90x＝1 210

C．130x＋90＝1 210  D．(130－90)x＝1 210

8.某人有连续4天的休假，这4天的日期之和是86，则休假第一天的日期是(　A　)

A．20日 B．21日 C．22日 D．23日

9.我国古代名著《九章算术》中有一题“今有凫起南海，七日至北海；雁起北海，九日至南海．今凫雁俱起，问何日相逢？”(凫：野鸭)设野鸭与大雁从南海和北海同时起飞，经过x天相遇，则可列方程为(　D　)

A．(9－7)x＝1 B．(9＋7)x＝1 C．x＝1 D．x＝1

10.公元前1700年的古埃及纸草书中,记载着一个数学问题:“它的全部,加上它的七分之一,其和等于19.”此问题中“它”的值为(   C   )

A.  B. C. D.

11.关于x的方程3－x＝2a与方程x＋3x＝28的解相同，则a的值为(　B　)

A．2 B．－2 C．5 D．－5

12.如图是日历表，任意圈出一竖列相邻的三个数，请你用方程的思想来研究，发现这三个数的和不可能是(　C　)

A．27 B．36 C．40 D．54

二、填空题

13.解方程6x＋9x－12x＝21＋3,合并同类项可得　3x＝24　,将未知数的系数化为1可得　x＝8　. 

14.小张有三种邮票共18枚,它们的数量之比为1∶2∶3,则最多的一种邮票有　9　枚. 

15.《孙子算经》中有这样一道题,原文如下:

今有百鹿入城,家取一鹿,不尽,又三家共一鹿,适尽,问城中家几何?

大意为:今有100头鹿进城,每家取一头鹿,没有取完,剩下的鹿每3家再共取一头,恰好取完,问:城中有多少户人家?设城中有x户人家,则可以列方程为　x＋x＝100　. 

16.若关于x的方程2mx＋3m＝－1与3x＋6x＝－3的解相同,则m的值为　－　. 

17.某校三年共购买计算机140台,去年购买的数量是前年的2倍,今年购买的数量是去年的2倍,则这个学校前年购买了　20　台计算机. 

18.已知＝1－;…则方程＋…＋＝2 021的解是　x＝2 022　. 

19.方程＋…＋＝2 020的解是　x＝8 088　. 

【提示】

三、解答题

20.解方程:

(1)3x＋2x－6x＝－9＋15;

解:合并同类项,得－x＝6.

系数化为1,得x＝－6.

(2)－1.4x＋2.8x＝－7＋9.8;

解:合并同类项,得1.4x＝2.8.

系数化为1,得x＝2.

(3)x－x＋x－x＝.

解:原方程可化为×,

系数化为1,得x＝.

21.一件夹克衫先按成本价提高60%标价,再将标价打7折出售,结果获利36元,则这件夹克衫的成本价是多少元?

解:设这件夹克衫的成本价是x元.

依题意,得0.7×(1＋60%)x－x＝36,解得x＝300.

答:这件夹克衫的成本价是300元.

22.用大小两台拖拉机耕地,每小时共耕地30亩.已知大拖拉机的工作效率是小拖拉机的1.5倍,问小拖拉机每小时耕地多少亩?

解:设小拖拉机每小时耕地x亩,则大拖拉机每小时耕地1.5x亩.

根据题意,得x＋1.5x＝30,解得x＝12.

答:小拖拉机每小时耕地12亩.

23.小莹花30元钱买了5千克苹果和2千克香蕉,找回3元.已知每千克香蕉的售价是每千克苹果售价的2倍,则每千克香蕉的售价是多少元?

售价的2倍,则每千克香蕉的售价是多少元?

解:设每千克香蕉的售价是x元,则每千克苹果的售价是元.

根据题意,得5×＋2x＝30－3,解得x＝6.

答:每千克香蕉的售价是6元.

24.甲、乙两人分别从相距1000米的A,B两地同时出发,相向而行,甲每秒走米,乙每秒走米.甲带一只狗和他同时出发,狗以每秒3米的速度向乙奔去,遇到乙后立即调转头向甲奔去,遇到甲后又调转头向乙奔去,直到甲、乙两人相遇时狗才停下,则这只狗一共跑了多少米?

解:设出发后甲、乙两人经过x秒相遇,则相遇时甲、乙两人所走的路程分别是x米.

根据题意,得x＝1000,解得x＝360.

360×3＝1080(米).

答:这只狗一共跑了1080米.

25.有一列数,按一定规律排列:1,－4,16,－64,256,－1024,…,其中有三个相邻的数的和是－13312,则这三个数分别是多少?

解:设相邻三个数中的第一个数为x,那么第二个数为－4x,第三个数为16x.

由题意得x－4x＋16x＝－13312,解得x＝－1024,

所以－4x＝4096,16x＝－16384.

答:这三个数分别是－1024,4096,－16384.

26.【江阴期中】将连续的奇数1，3，5，7…排列成如下的数表，用十字框框出5个数(如下图)．

(1)若将十字框上下左右平移，使得十字框正好框住数列中的5个数．小明发现这五个数的和总等于中间数的整数倍．若设中间的数为a，则框住的5个数字之和为5a    (用a的代数式表示)；

(2)在(1)的条件下，是否存在a的值，使得该十字框框住的5个数之和恰好等于2 020？若存在，求出此时a的值；若不存在，请说明理由；

(3)在(1)的条件下，十字框框住的5个数之和能等于415吗？若能，分别写出十字框框住的这5个数；若不能，请说明理由．

解：(1)由图知道中间的数为a，上面的数为a－12，下面的数为a＋12，左面的数为a－2，右面的数为a＋2，

a＋(a－2)＋(a＋2)＋(a－12)＋(a＋12)＝5a.故答案为5a.

(2)不存在．理由：依题意有5a＝2 020，解得a＝404，

∵404是偶数，

∴不存在a值使得十字框框住的5个数之和恰好为2 020.

(3)不能．理由：依题意有5a＝415，解得a＝83，

∵83位于一行的最右边，

∴十字框框住的5个数之和不能等于415.