2022-2023学年苏教版（2019）必修二第十三章 立体几何初步 单元测试卷

第十三章 立体几何初步 单元测试卷

学校：___________姓名：___________班级：___________考号：___________

一、选择题(共32分)

1、(4分)已知圆锥的顶点为S ，两条母线为SA,SB ，若 的面积为 与圆锥的底面所成的角为 ，则圆锥的体积为(   )
A.  B.  C.  D.

2、(4分)已知三棱锥中,分别是的平分线,平面,则直线所成角的余弦值为(   )

A. B. C. D.

3、(4分)在中，已知.现将绕边旋转一周，则所得到的旋转体的表面积是（   ）

A. B. C. D.

4、(4分)已知P是所在平面外的一点，分别是的中点，若，则异面直线与所成角的大小是(   )

A．30°       B．45°       C．60°       D．90°

5、(4分)已知圆锥的底面半径为2,高为1,经过圆锥顶点的平面α截此圆锥所得的截面面积为,则平面α与底面所成的锐二面角的正切值为(   )

A. B.1 C.或 D.或1

6、(4分)已知正三棱锥的六条棱长均为6，S是及其内部的点构成的集合，设集合，则T表示的区域的面积为(   )

A. B.π C. D.

7、(4分)在正三棱锥中，分别是棱、的中点，且，若侧棱，则正三棱锥外接球的体积是（    ）

A． B． C． D．

8、(4分)已知圆锥的表面积为，它的侧面展开图是一个半圆，则此圆锥的体积为（    ）

A. B. C. D.

二、多项选择题(共24分)

9、(6分)把一张长为4宽为3的矩形白纸卷成圆柱（缝隙忽略不计），圆柱的体积是（   ）

A. B. C. D.

10、(6分)已知平面平面.直线平面，直线平面，在下列说法中，正确的有(   )

A.若，则  B.若，则

C.若，则  D.则

11、(6分)等腰直角三角形的直角边长为1，现将该三角形绕其某一边旋转一周，则形成的几何体的表面积可以为(   )

A. B. C. D.

12、(6分)已知圆上的点到直线的距离等于,那么的值可以是(   )　　

A.               B.             C.            D.

三、填空题(共16分)

13、(4分)已知正方体的外接球与内切球上各有一个动点P,Q,若线段PQ的最小值为,则正方体的棱长为_________；正方体的外接球的表面积为_______.

14、(4分)三棱锥的顶点均在球O的球面上，且，，，则三棱锥体积的最大值为__________.

15、(4分)三棱锥的底面是边长为3的正三角形，面PAB垂直底面ABC，且，则三棱锥体积的最大值是_______.

16、(4分)在空间四边形ABCD中，，，E，F分别是AB，CD的中点，，则异面直线AD与BC所成角的大小为____.

四、解答题(共28分)

17、(14分)如图所示多面体中, 底面 是边长为 3 的正方形, 上平面 是 上一点,.

(1)求证: 平面;
(2)求此多面体的体积.

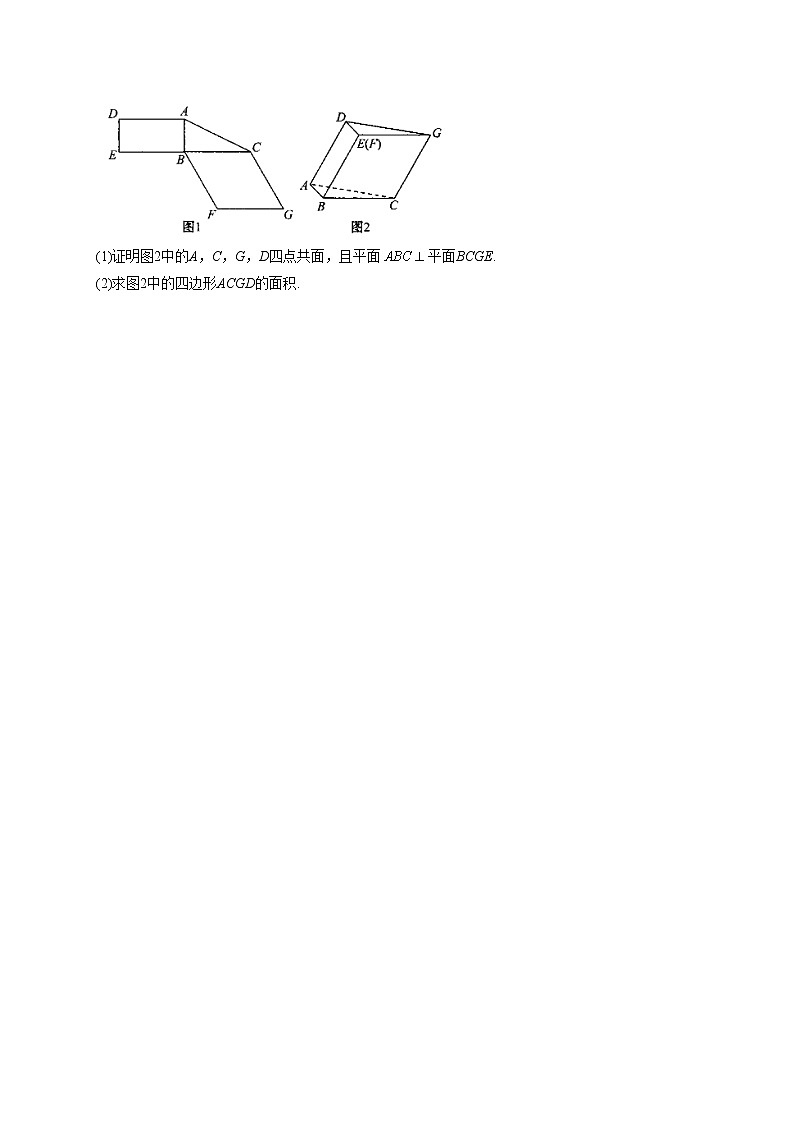
18、(14分)图1是由矩形ADEB、和菱形BFGC组成的一个平面图形，其中.将其沿AB，BC折起使得BE与BF重合，连接DG，如图2.

(1)证明图2中的A，C，G，D四点共面，且平面平面BCGE.

(2)求图2中的四边形ACGD的面积.

参考答案

1、答案：B

解析：

2、答案：D

解析：本题考查空间线面的位置关系、空间角的计算.因为平面平面,所以.又平面,故平面,所以, ,又,故.同理可得,,又,所以,故三棱锥为正四面体.

如图,取的中点G,连接,则,故即为与所成角或其补角,设,则,,

在中,由余弦定理得,

故直线所成角的余弦值为,故选D.

3、答案：D

解析：

4、答案：A

解析：

5、答案：D

解析：如图,设圆锥的顶点为P,底面圆的圆心为O,平面α与圆O的交点分别为,过点P作于点H,连接.由题意可知,平面α截此圆锥所得的截面为等腰三角形,且点H为的中点.设,则在中,,在中,,所以的面积.整理,得,解得或(负值已舍去).因为平面α与底面所成的锐二面角即为,所以或.故选D.

6、答案：B

解析：设O为的中心，连接PO，AO，在正三角形ABC中，，在中，，当时，连接OQ，根据勾股定理可得，易知Q的轨迹是以O为圆心，半径为1的圆，由于集合，故集合T表示的区每的面积为π，故选B.

7、答案：A

解析：

8、答案：A

解析：设圆锥的底面半径为 ，高为 ，母线为，
因为其表面积为 ，
所以 ，
即
又因为它的侧面展开图是一个半圆，
所以 ，
即
所以 ，
所以此圆锥的体积为.
故选: A

9、答案：CD

解析：若底面周长为，则，，圆柱体积.

若底面周长为，则，，圆柱体积.

故选：CD

10、答案：BC

解析：

11、答案：AB

解析：如果绕直角边旋转，形成圆锥，圆锥底面半径为1，高为1，母线长为，所以所形成的几何体的表面积.如果绕斜边旋转，形成的是上下两个圆锥，圆锥的半径长等于直角三角形斜边上的高，为，两个圆锥的母线长都等于直角三角形的直角边长，所以形成的几何体的表面积.综上可知，形成几何体的表面积是或.故选AB.

12、答案：ABC

解析：圆 的圆心为 ，半径为 2 .

直线 过 ，
与 的距离为 ，
所以 的取值范围是 ，
所以ABC 选项符合， D选项不符合.
故选 : ABC.

13、答案：4   

解析：

14、答案：2

解析：

15、答案：

解析：

16、答案：

解析：解：取AC中点O，连接EO，FO.

在空间四边形ABCD中，，，E，F分别是AB，CD的中点，，，，，，是异面直线AD与BC所成角（或所成角的补角），，，异面直线AD与BC所成角的大小为.

17、答案：(1)见解析(2)

解析：(1) 证明: 过点 作, 交 于点, 则

因为, 所以, 且, 所以四边形 为平行四边形,所以. 又 平面 丈平面, 所以 平面.

(2) 因为 平面 平面, 所以, 因为, 所以 平面.
所以, ,
即此多面体的体积为

18、答案：(1)见解析.

(2)面积为4.

解析：(1)由已知得，

所以，故AD，CG确定一个平面，从而A，C，G，D四点共面.

由已知得，故平面BCGE.

又因为平面ABC，所以平面平面BCGE.

(2)取CG的中点M，连接EM，DM.

因为平面BCGE，

所以平面BCGE，故.

由已知，四边形BCGE是菱形且得，

故平面DEM.

因此.

在中，，故.

所以四边形ACGD的面积为4.