
- 1.5.1全称量词与存在量词--2022-2023学年高一数学新教材同步(教学设计)(人教A版2019必修第一册) 教案 2 次下载
- 1.5.2全称量词与存在量词命题的否定--2022-2023学年高一数学新教材同步(教学设计)(人教A版2019必修第一册) 教案 3 次下载
- 2.2基本不等式(第1课时)--2022-2023学年高一数学新教材同步(教学设计)(人教A版2019必修第一册) 教案 2 次下载
- 2.2基本不等式(第2课时)--2022-2023学年高一数学新教材同步(教学设计)(人教A版2019必修第一册) 教案 2 次下载
- 2.3二次函数与一元二次方程、不等式--2022-2023学年高一数学新教材同步(教学设计)(人教A版2019必修第一册) 教案 2 次下载
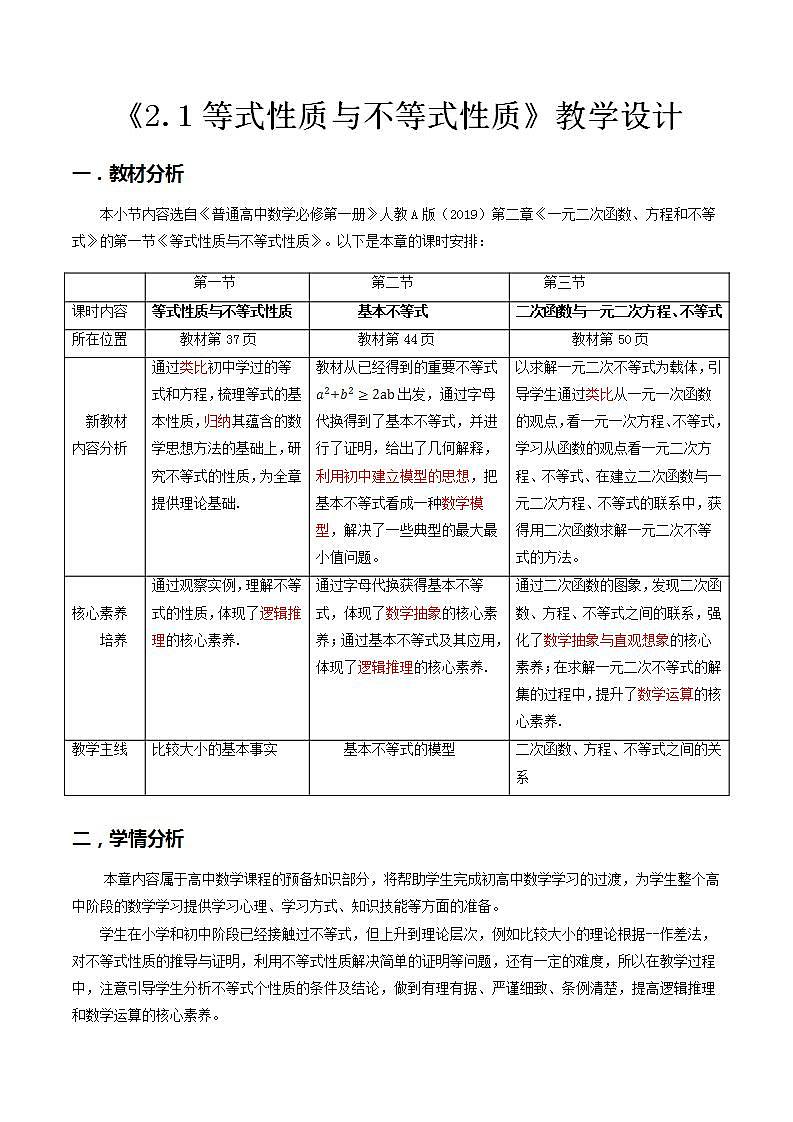
数学2.1 等式性质与不等式性质教案及反思
展开《2.1等式性质与不等式性质》教学设计
一.教材分析
本小节内容选自《普通高中数学必修第一册》人教A版(2019)第二章《一元二次函数、方程和不等式》的第一节《等式性质与不等式性质》。以下是本章的课时安排:
| 第一节 | 第二节 | 第三节 |
课时内容 | 等式性质与不等式性质 | 基本不等式 | 二次函数与一元二次方程、不等式 |
所在位置 | 教材第37页 | 教材第44页 | 教材第50页 |
新教材 内容分析 | 通过类比初中学过的等式和方程,梳理等式的基本性质,归纳其蕴含的数学思想方法的基础上,研究不等式的性质,为全章提供理论基础. | 教材从已经得到的重要不等式+出发,通过字母代换得到了基本不等式,并进行了证明,给出了几何解释,利用初中建立模型的思想,把基本不等式看成一种数学模型,解决了一些典型的最大最小值问题。 | 以求解一元二次不等式为载体,引导学生通过类比从一元一次函数的观点,看一元一次方程、不等式,学习从函数的观点看一元二次方程、不等式、在建立二次函数与一元二次方程、不等式的联系中,获得用二次函数求解一元二次不等式的方法。 |
核心素养培养 | 通过观察实例,理解不等式的性质,体现了逻辑推理的核心素养. | 通过字母代换获得基本不等式,体现了数学抽象的核心素养;通过基本不等式及其应用,体现了逻辑推理的核心素养. | 通过二次函数的图象,发现二次函数、方程、不等式之间的联系,强化了数学抽象与直观想象的核心素养;在求解一元二次不等式的解集的过程中,提升了数学运算的核心素养. |
教学主线 | 比较大小的基本事实 | 基本不等式的模型 | 二次函数、方程、不等式之间的关系 |
二,学情分析
本章内容属于高中数学课程的预备知识部分,将帮助学生完成初高中数学学习的过渡,为学生整个高中阶段的数学学习提供学习心理、学习方式、知识技能等方面的准备。
学生在小学和初中阶段已经接触过不等式,但上升到理论层次,例如比较大小的理论根据--作差法,对不等式性质的推导与证明,利用不等式性质解决简单的证明等问题,还有一定的难度,所以在教学过程中,注意引导学生分析不等式个性质的条件及结论,做到有理有据、严谨细致、条例清楚,提高逻辑推理和数学运算的核心素养。
三.学习目标
1. 掌握等式性质与不等式性质以及推论,培养学生数学抽象的核心素养;
2. 进一步掌握作差比较法比较实数的大小,提升数学运算的核心素养;
3. 能利用不等式的性质证明简单的不等式、求代数式的取值范围,强化逻辑推理的核心素养。
四.教学重点
重点:掌握不等式性质及其应用.
难点:类比等式的基本性质及其蕴含的思想方法,研究不等式的基本性质;
等式与不等式的共性与差异.
五.教学过程
(一)新知导入
1. 创设情境,生成问题
在日常生活中,购买火车票有一项规定:随同成人旅行,身高超过1.2 m(含1.2 m)而不超过1.5 m的儿童,享受半价客票、加快票和空调票(简称儿童票),超1.5 m时应买全价票. 每一成人旅客可免费携带一名身高不足1.2米的儿童,超过一名时,超过的人数应买儿童票.
【想一想】 设儿童的身高为米,如何利用不等式或不等式组来表示“身高超过1.2 m(含1.2 m)而不超过1.5 m”、“身高超1.5 m”和“身高不足1.2米”呢?
【提示】
- 探索交流,解决问题
日常生活中的多与少、大与小、长与短、高与矮、远与近、快与慢、涨与跌、轻与重等问题,反映在数量关系上,就是相等与不等。相等用等式表示,不等用不等式表示。
【设计意图】
通过探究,引导学生发现生活中的相等关系与不等关系,并能用数学式子表示出来,提高学生用数学抽象的思维方式思考并解决问题的能力。
(二)不等式与不等关系
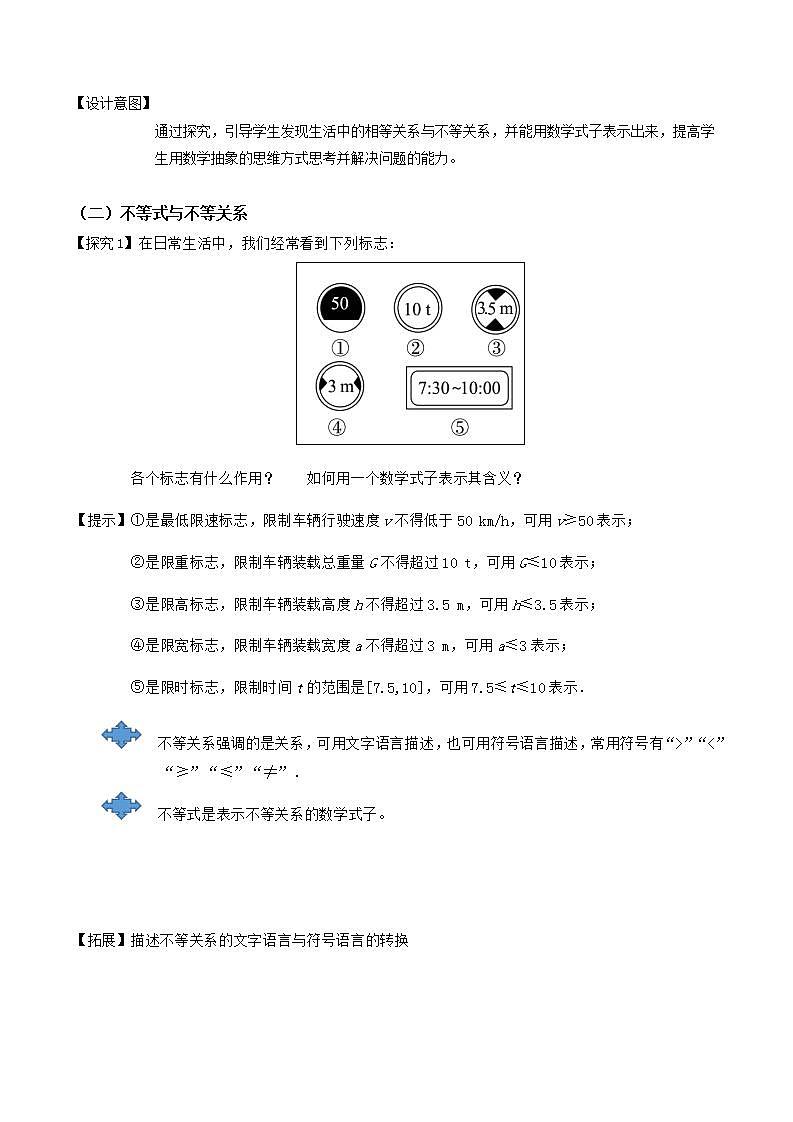
【探究1】在日常生活中,我们经常看到下列标志:
各个标志有什么作用? 如何用一个数学式子表示其含义?
【提示】①是最低限速标志,限制车辆行驶速度v不得低于50 km/h,可用v≥50表示;
②是限重标志,限制车辆装载总重量G不得超过10 t,可用G≤10表示;
③是限高标志,限制车辆装载高度h不得超过3.5 m,可用h≤3.5表示;
④是限宽标志,限制车辆装载宽度a不得超过3 m,可用a≤3表示;
⑤是限时标志,限制时间t的范围是[7.5,10],可用7.5≤t≤10表示.
不等关系强调的是关系,可用文字语言描述,也可用符号语言描述,常用符号有“>”“<”“≥”“≤”“≠”.
不等式是表示不等关系的数学式子。
【拓展】描述不等关系的文字语言与符号语言的转换
文字语言 | 大于,高于,超过 | 小于,低于,少于 | 大于等于,至少,不少于,不低于 | 小于等于,至多,不多于,不超过 |
符号语言 | > | < | ≥ | ≤ |
【探究2】如图是在北京召开的第24界国际数学家大会的会标,会标是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去象一个风车,代表中国人民热情好客.你能在这个图案中找出一些相等关系或不等关系吗?
【提示】如上图,设大正方形四个角上的直角三角形的两个直角边分别为,
则大正方形的面积为,四个矩形的面积和为,
显然,大正方形的面积大于等于四个矩形的面积和,所以
所以a2+b2≥2ab.
例1. 用一段长为30 m的篱笆围成一个一边靠墙的矩形菜园,墙长18 m,要求菜园的面积不小于
110 m2,靠墙的一边长为x m. 试用不等式表示其中的不等关系.
[解析] 由于矩形菜园靠墙的一边长为x m,而墙长为18 m,所以0<x≤18,
这时菜园的另一条边长为=m.
因此菜园面积S=x·.
依题意有S≥110,即x≥110,
故该题中的不等关系可用不等式表示为
【类题通法】
1.不等式(组)表示实际问题中不等关系的步骤
(1)审题.通读题目,分清楚已知量和待求量,设出待求量;
(2)列不等关系.列出待求量具备哪些不等关系(即满足什么条件);
(3)列不等式(组).挖掘题意,建立已知量和待求量之间的关系式,并分析某些变量的约束条件(包含隐含条件).
2.用不等式表示不等关系的注意点
(1)利用不等式表示不等关系时,应注意必须是具有相同性质,可以比较大小的两个量才可用,没有可比性的两个量之间不能用不等式来表示.
(2)在用不等式表示实际问题时,一定要注意单位统一.
【巩固练习1】 一辆汽车原来每天行驶x km,如果该汽车每天行驶的路程比原来多19 km,那么在8天内它的行程将超过2 200 km,用不等式表示为________.
[解析] 因为该汽车每天行驶的路程比原来多19 km,所以汽车每天行驶的路程为(x+19)km,则在8天内它的行程为8(x+19)km,因此,不等关系“在8天内它的行程将超过2 200 km”可以用不等式8(x+19)>2 200来表示.
[答案] 8(x+19)>2 200
(三)比较大小的基本事实
【探究3】我们知道,实数可以用数轴上的点表示,数轴上的每个点都表示一个实数,且右边的点表示的实数比左边的点表示的实数大.对于两个实数a,b,它们的大小关系有几种?怎样判断?
【提示】对于两个实数a,b,它们的大小关系有3种,如果a-b是正数,那么a>b;如果a-b是负数,那么a<b;如果a-b是零,那么a=b.
如果a-b是正数,那么;如果a-b等于0,那么;如果a-b是负数,那么.反过来也对.这个基本事实可以表示为:
例2. (2021·陕西咸阳市实验中学高二月考)
(1)已知实数比较+与+大小.
(2)已知a>0,试比较a与的大小.
【思维引导】将两式作差,化简,分析差的符号得到大小关系。
[解析](1)
又,而
故即
(2)a-==.
∵a>0,∴当a>1时,>0,有;
当a=1时,=0,有;
当0<a<1时,<0,有.
综上,当时,;当时,;
当时,.
【类题通法】比较两个代数式大小的步骤
(1)作差:对要比较大小的两个数(或式子)作差;
(2)变形:对差进行变形;
(3)判断差的符号:结合变形的结果及题设条件判断差的符号;
(4)作出结论.
[提醒] 上述步骤可概括为“三步一结论”,这里的“判断符号”是目的,“变形”是关键.其中变形的技巧较多,常见的有因式分解法、配方法、有理化法等.
【巩固练习2】已知x<1,试比较x3-1与2x2-2x的大小.
[解析] (x3-1)-(2x2-2x)
=x3-2x2+2x-1=(x3-x2)-(x2-2x+1)
=x2(x-1)-(x-1)2=(x-1)(x2-x+1)
=(x-1).
∵2+>0,x-1<0,
∴(x-1)<0,
∴x3-1<2x2-2x.
【设计意图】
通过例题及练习,使学生熟练比较大小的方法及过程,培养数学运算的核心素养。
(四)等式性质
【探究4】如何求方程5x+4=0的解?解方程的理论依据是什么?
【提示】先将等式两边同时减4,得
再将等式两边同时除以5,得,
所以方程的解是.
解方程的理论依据是等式的性质。
等式性质
性质1 如果那么(对称性)
性质2 如果那么(传递性)
性质3 如果那么
性质4 如果那么
性质5 如果那么
性质3,4,5是等式对四则运算的不变性.
【做一做】下列运用等式的性质,变形不正确的是( )
A.若,则
B.若,则
C.若,则
D.若,则
[答案] D
(五)不等式性质
【探究5】 (1)如果甲同学比乙同学大,那么乙同学比甲同学小,对吗?
(2)如果甲同学比乙同学大,且乙同学比丙同学大,那甲同学比丙同学大,对吗?
(3)如果,那么a+c与b+c的大小关系如何?ac与bc呢?
(4)不等式还有哪些性质?
【提示】 (1), (2)对;
(3)如果.
当时,;当时,;当时,.
不等式性质
性质1 如果如果,那么.
性质2 如果,那么(传递性)
符号表示:
性质3 如果,那么
文字表示:不等式的两边都加上同一个实数,所得不等式与原不等式同向.
移项法则:
性质4 如果那么; 如果那么
文字表示:不等式的两边同乘一个正数,所得不等式与原不等式同向;不等式的两边同乘一个负数,所得不等式与原不等式反向.
性质5 如果,那么
注意:同向不等式相加得同向不等式,并无相减。
性质6 如果,那么
注意:同向不等式相乘得同向不等式,并无相除。另外“大于0”的条件不能忽略。
性质7 如果那么.
注意:“大于0”的条件不能忽略。
重要结论:如果,那么,如果那么.
(六)不等式性质的应用
- 判断不等式是否成立
例3. 如果a,b,c满足,且,那么下列不等式中不一定成立的是( )
[解析] 由于且,因此,b的符号不确定,则不一定成立的不等式可能与b有关.不难发现,当C中的b为0时,不等式不成立.
[答案] C
【类题通法】利用不等式判断正误的2种方法
(1)直接法:对于说法正确的,要利用不等式的相关性质证明;对于说法错误的只需举出一个反例即可.
(2)特殊值法:注意取值一定要遵循三个原则:一是满足题设条件;二是取值要简单,便于验证计算;三是所取的值要有代表性.
【巩固练习3】(多选题)若,则下列命题:
(1) . (2). (3). (4)
中能成立的是( )
A.(1) B.(2) C.(3) D.(4)
[解析] 因为a>0>b,c<d<0,所以ad<0,bc>0,所以ad<bc,所以(1)错误.
因为a>0>b>-a,所以a>-b>0,因为c<d<0,所以-c>-d>0,所以a(-c)>(-b)(-d),
所以ac+bd<0,所以,所以(2)正确.
因为c<d,所以-c>-d,因为a>b,所以a+(-c)>b+(-d),即a-c>b-d,所以(3)正确.
因为a>b,d-c>0,所以a(d-c)>b(d-c),所以(4)正确.
[答案] BCD
- 证明不等式
例4. 已知, 求证:.
证明:法一:
又,
∴.
,∴上式同乘e得,不等式得证.
法二:-=
=.
∵
∴
∵,∴,
∴
【类题通法】利用不等式的性质证明不等式应注意的事项
(1) 利用不等式的性质及其推论可以证明一些不等式.解决此类问题一定要在理解的基础上,记准、记熟不等式的性质并注意在解题中灵活准确地加以应用.
(2) 应用不等式的性质进行推导时,应注意紧扣不等式的性质成立的条件,且不可省略条件或跳步推导,更不能随意构造性质与法则.
【巩固练习4】 已知,求证:.
证明:∵c>a>b>0,∴c-a>0,c-b>0,
⇒<
⇒>.
3.利用不等式性质求取值范围
例5.已知1<a<4,2<b<8,试求2a+3b与a-b的取值范围.
【思维引导】欲求2a+3b与a-b的取值范围,先求 的取值范围,再利用不等式的性质求解。
[解析] ∵1<a<4,2<b<8,∴2<2a<8,6<3b<24.
∴8<2a+3b<32.
∵2<b<8,∴-8<-b<-2.
又∵1<a<4,∴1+(-8)<a+(-b)<4+(-2),
即-7<a-b<2.
故2a+3b的取值范围是8<2a+3b<32,a-b的取值范围是-7<a-b<2.
【类题通法】利用不等式的性质求取值范围的策略
(1) 建立待求范围的整体与已知范围的整体的关系,最后利用一次不等式的性质进行运算,求得待求的范围.
(2) 同向(异向)不等式的两边可以相加(相减),这种转化不是等价变形,如果在解题过程中多次使用这种转化,就有可能扩大其取值范围.
[提醒] 求解这种不等式问题要特别注意不能简单地分别求出单个变量的范围,再去求其他不等式的范围.
【巩固练习5】
已知-1≤a+b≤1,1≤a-2b≤3,求a+3b的取值范围.
[解析] 设a+3b=λ(a+b)+(a-2b)=(λ+)a+(λ-2)b,解得λ=,=-.
又-≤(a+b)≤,-2≤-(a-2b)≤-,
所以-≤a+3b≤1.
【设计意图】通过不等式的判断、证明,使学生熟练掌握不等式的性质,培养学生解决问题的能力。
(七)操作演练 素养提升
1. 完成一项装修工程,请木工共需付工资每人500元,请瓦工共需付工资每人400元,现有工人工资预算
20000元,设木工x人,瓦工y人,则工人满足的关系式是( )
A.5x+4y<200 B.5x+4y≥200
C.5x+4y=200 D.5x+4y≤200
2.若x∈R,y∈R,则下列关系正确的是( )
A.x2+y2>2xy-1 B.x2+y2=2xy-1
C.x2+y2<2xy-1 D.x2+y2≤2xy-1
3.下列命题中正确的是( )
A.若a>b,c>d,则ac>bd B.若ac>bc,则a>b
C.若<,则a<b D.若a>b,c>d,则a-c>b-d
4.给出下列命题:
①若ab>0,a>b,则;
②若a>b,c>d,则a-c>b-d;
③对于正数a,b,m,若a<b,则.
其中真命题的序号是________.
[答案] 1.D 2.A 3.C 4.①③
【设计意图】通过练习巩固本节所学知识,通过学生解决问题的能力,感悟其中蕴含的数学思想,增强学生的应用意识。
(六)课堂小结,反思感悟
1.知识总结:
2.学生反思:
(1)通过这节课,你学到了什么知识?
(2)在解决问题时,用到了哪些数学思想?
【设计意图】
通过总结,让学生进一步巩固不等式的性质,辨析不等式成立的条件,树立用不等式解决相关问题的意识。
六.布置作业
完成教材: 第39页 练习 第1,2,3题
第42页 练习 第2 题
第42页 习题2.1 第2,3,5,6,7,8题
数学必修 第一册2.1 等式性质与不等式性质教案: 这是一份数学必修 第一册2.1 等式性质与不等式性质教案,共23页。
必修 第一册第二章 一元二次函数、方程和不等式2.1 等式性质与不等式性质教学设计: 这是一份必修 第一册第二章 一元二次函数、方程和不等式2.1 等式性质与不等式性质教学设计,共4页。教案主要包含了目标及其解析,课时教学设计等内容,欢迎下载使用。
人教A版 (2019)必修 第一册5.1 任意角和弧度制教学设计及反思: 这是一份人教A版 (2019)必修 第一册5.1 任意角和弧度制教学设计及反思,共9页。教案主要包含了教材分析,学情分析,学习目标,教学重点,教学过程,布置作业等内容,欢迎下载使用。