高中数学人教A版 (2019)必修 第一册第二章 一元二次函数、方程和不等式2.2 基本不等式第2课时教案设计

《2.2基本不等式》

第2课时  基本不等式的综合应用 教学设计

一．教材分析

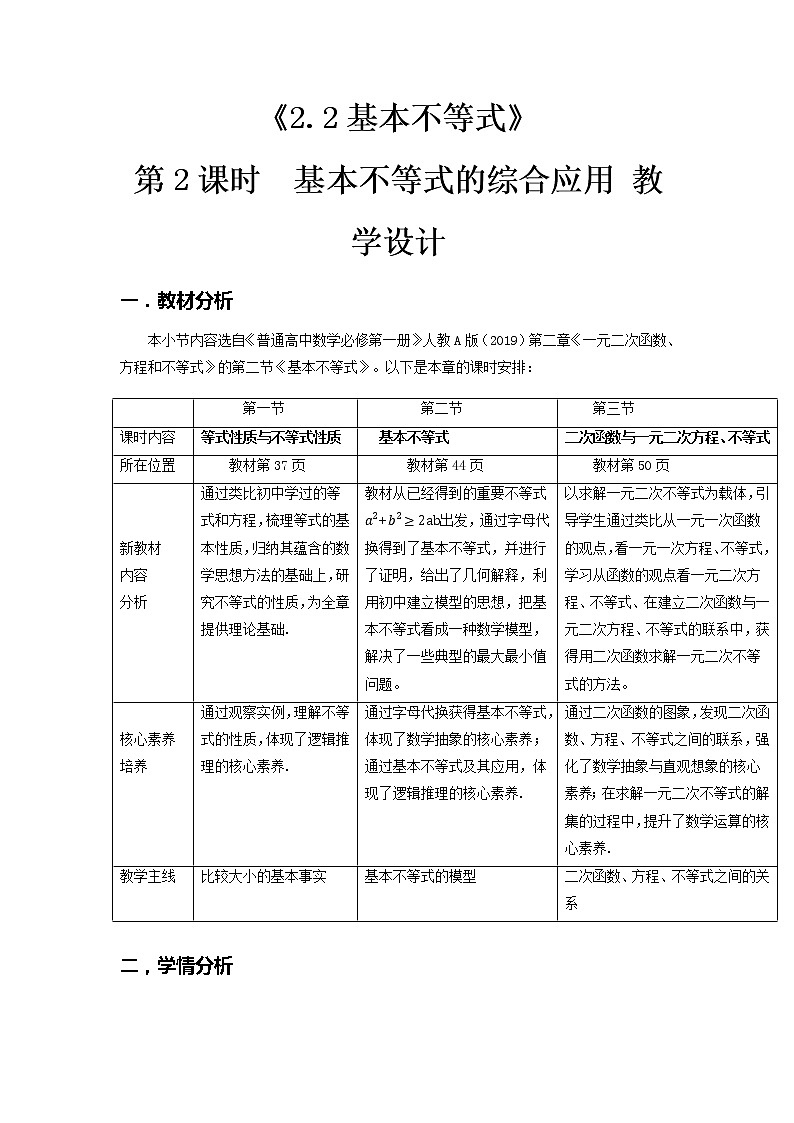
本小节内容选自《普通高中数学必修第一册》人教A版（2019）第二章《一元二次函数、方程和不等式》的第二节《基本不等式》。以下是本章的课时安排：

二，学情分析

     本章内容属于高中数学课程的预备知识部分，将帮助学生完成初高中数学学习的过渡，为学生整个高中阶段的数学学习提供学习心理、学习方式、知识技能等方面的准备。

学生在上一节学习了基本不等式的定义及简单应用，本节课是上一节内容的延伸，解决求最值过程中的易犯错误的处理方法，并求解了实际应用问题中的最值，所以学生学习本节内容还是比较有兴趣的，本节知识渗透了数学运算、逻辑推理、数学建模等核心素养，有利于培养学生良好的思维品质。

三．学习目标

1. 通过实例，掌握基本不等式及应用，培养学生数学抽象的核心素养；

2. 能够利用基本不等式求函数或代数式的最值，提升数学运算和逻辑推理的核心素养；             

3. 会利用基本不等式求解实际问题中的最值，强化数学运算的核心素养。

四．教学重点

重点：利用基本不等式求最值；

利用基本不等式解决实际应用问题．

难点：基本不等式的应用；

基本不等式求最值．

五．教学过程

（一）新知导入

1. 创设情境，生成问题

 根据上一节课的知识，我们了解了基本不等式与最值的关系，如下：已知x，y都是正数，则

①如果积xy等于定值P(积为定值)，那么当x＝y时，和x＋y有最小值2.

②如果和x＋y等于定值S(和为定值)，那么当x＝y时，积xy有最大值S2.

【想一想】下面这些结论是否正确？

(1)若a>0，b>0，且a＋b＝16，则ab≤64.(　　)

(2)若ab＝2，则a＋b的最小值为2.(　　)

(3)当x>1时，函数y＝x＋≥2，所以函数y的最小值是2.(　　)

(4)若x∈R，则x2＋2＋≥2.(　　)

【提示】（1）正确；（2）错误；（3）错误；（4）错误.

2. 探索交流，解决问题

 利用基本不等式求最大值或最小值时应注意：

(1)x，y一定要都是正数；

(2)求积xy最大值时，应看和x＋y是否为定值；求和x＋y最小值时，应看积xy是否为定值；

(3)等号是否能够成立．

以上三点可简记为“一正、二定、三相等”.

【设计意图】

通过探究，引导学生发现利用基本不等式求最值时的常见错误，在此基础上引导学生总结利用基本不等式求最值需要注意的问题，提高学生用数学抽象的思维方式思考并解决问题的能力。

（二）基本不等式求最值

1.配凑法

例1.(1)若x＜0，求＋3x的最大值；

(2)若x＞2，求＋x的最小值；

(3)已知0＜x＜，求x(1－2x)的最大值．

[解析]　(1)因为x＜0，

所以＋3x＝－

≤－2＝－12，

当且仅当－＝－3x，即x＝－2时等号成立，

所以＋3x的最大值为－12.

(2)因为x＞2，所以x－2＞0，＋x＝＋x－2＋2≥2＋2＝4，当且仅当x－2＝，即x＝3时等号成立，所以＋x的最小值为4.

(3)因为0＜x＜，所以1－2x＞0，

x(1－2x)＝·2x(1－2x)≤2＝，

当且仅当2x＝1－2x，即x＝时等号成立，所以x(1－2x)的最大值为.

【类题通法】利用基本不等式求最值的关键是获得定值条件，解题时应对照已知和欲求的式子运用适当的“拆项、添项、配凑、变形”等方法创设应用基本不等式的条件．

【巩固练习1】已知x＜，求4x－2＋的最大值

[解析]　（1）因为x＜，所以4x－5＜0，则5－4x＞0，

所以4x－2＋＝4x－5＋＋3.

因为5－4x＋≥2＝2，所以4x－5＋≤－2.

所以4x－5＋＋3≤－2＋3＝1.

当且仅当5－4x＝，即x＝1时，等号成立．

故当x＝1时，4x－2＋取最大值1.

2.常值代换

例2.已知x＞0，y＞0，且＋＝1，求x＋y的最小值．

[解析]　∵x＞0，y＞0，＋＝1，

∴x＋y＝(x＋y)＝＋＋10≥2＋10＝6＋10＝16，

当且仅当＝，＋＝1，

即x＝4，y＝12时，上式取等号．

故当x＝4，y＝12时，x＋y的最小值是16.

【类题通法】

这种方法常用于“已知ax＋by＝m(a，b，x，y均为正数)，求＋的最小值”和“已知＋＝1(a，b，x，y均为正数)，求x＋y的最小值”两类题型．

【巩固练习2】　（2021·阜阳市耀云中学高二期中）已知x>0，y>0，且，则x+y的最小值是（　　）

A．10 B．15 C．18 D．23

[解析]  由x>0，y>0，且，得，

所以，

当且仅当，即时等号成立，所以的最小值是18．

[答案]  C

【设计意图】通过基本不等式求最值，使学生熟练掌握基本不等式求最值的方法，培养学生逻辑推理和数学运算的核心素养。

（三）利用基本不等式求实际问题的最值

例3.如图，动物园要围成相同面积的长方形虎笼四间，一面可利用原有的墙，其他各面用钢筋网围成．

(1)现有可围 36 m长网的材料，每间虎笼的长、宽各设计为多少时，可使每间虎笼面积最大？

(2)若使每间虎笼面积为24 m2，则每间虎笼的长、宽各设计为多少时，可使围成四间虎笼的钢筋网总长最小？

【思维引导】　设每间虎笼长x m，宽y  m，则

问题（1）是在4x＋6y＝36的前提下求xy的最大值．

问题（2）是在xy＝24的前提下求4x＋6y的最小值．

[解析]　(1)设每间虎笼长x  m，宽为y  m，则由条件知4x＋6y＝36，即2x＋3y＝18.

设每间虎笼面积为S，则S＝xy.

由于2x＋3y≥2＝2，

∴2≤18，得xy≤，

即S≤，当且仅当2x＝3y时，等号成立．

由解得

故每间虎笼长为4.5 m，宽为3 m时，可使面积最大．

(2)由条件知S＝xy＝24.

设钢筋网总长为l，则l＝4x＋6y.

∵2x＋3y≥2＝2＝24，

∴l＝4x＋6y＝2(2x＋3y)≥48，当且仅当2x＝3y时，等号成立．

由解得

故每间虎笼长6 m，宽4 m时，可使钢筋网总长最小．

【类题通法】求实际问题中最值的解题4步骤

(1)先读懂题意，设出变量，理清思路，列出函数关系式．

(2)把实际问题抽象成函数的最大值或最小值问题．

(3)在定义域内，求函数的最大值或最小值时，一般先考虑基本不等式．

(4)回到实际问题中，正确写出答案．　　

【巩固练习3】围建一个面积为360 m2的矩形场地，要求矩形场地的一面利用旧墙(利用的旧墙需维修)，其他三面围墙要新建，在旧墙对面的新墙上要留一个宽度为2 m的进出口，如图．已知旧墙的维修费用为45 元/m，新墙的造价为180 元/m.设利用的旧墙长度为x(单位：m)，修建此矩形场地围墙的总费用为y(单位：元)．

试确定x，使修建此矩形场地围墙的总费用最小，并求出最小总费用．

[解析]　设矩形的另一边长为a m，

则y＝45x＋180(x－2)＋180×2a＝225x＋360a－360.

由已知xa＝360，得a＝，

∴y＝225x＋－360.

∵x>0，

∴225x＋≥2＝10 800.

∴y＝225x＋－360≥10 440.

当且仅当225x＝时，等号成立．

即当x＝24 m时，修建围墙的总费用最小，最小总费用是10 440元．

【设计意图】通过基本不等式求解实际应用问题的最值，使学生熟练掌握基本不等式求最值的方法，培养学生数学建模的核心素养。

（四）操作演练  素养提升

1.设x>0，则3－3x－的最大值是(　　)

A．3   B．3－2

C．－1   D．3－2

2．当x>1时，则2x＋的最小值为          

3.函数y＝(x＞－1)的最小值为________．

4.已知正数a，b满足a＋2b＝2，则＋的最小值为________．

[答案]   1.D   2.10     3.0    4.4

【设计意图】通过练习巩固本节所学知识，通过学生解决问题的能力，感悟其中蕴含的数学思想，增强学生的应用意识。

（六）课堂小结，反思感悟

 1.知识总结：

2.学生反思：

（1）通过这节课，你学到了什么知识？

（2）在解决问题时，用到了哪些数学思想？

【设计意图】

通过总结，让学生进一步巩固基本不等式，辨析基本不等式求最值时需要注意的问题,树立用基本不等式解决相关问题的意识。

六．布置作业

完成教材：第48页  练习     第1，2，3,4题

 第48页   习题2.2   第1，3，5，6，7，8题