人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直教学课件ppt

这是一份人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直教学课件ppt，共35页。PPT课件主要包含了必备知识生成，一个平面内，关键能力探究，平面与平面垂直二，课堂素养达标等内容，欢迎下载使用。

【情境探究】1.教室内的黑板所在的平面与地面所在的平面垂直,在黑板上任意画一条直线与地面垂直吗?怎样画才能保证所画直线与地面垂直?提示:不一定,也可能平行,相交(不垂直);只要保证所画的线与两面的交线垂直即可.
2.如图长方体ABCD -A′B′C′D′,在平面DCC′D′中,作直线l⊥DC.你能得出什么结论? 提示:在平面DCC′D′内,若直线l垂直于交线DC,则直线l垂直于平面ABCD.
【知识生成】平面与平面垂直的性质定理
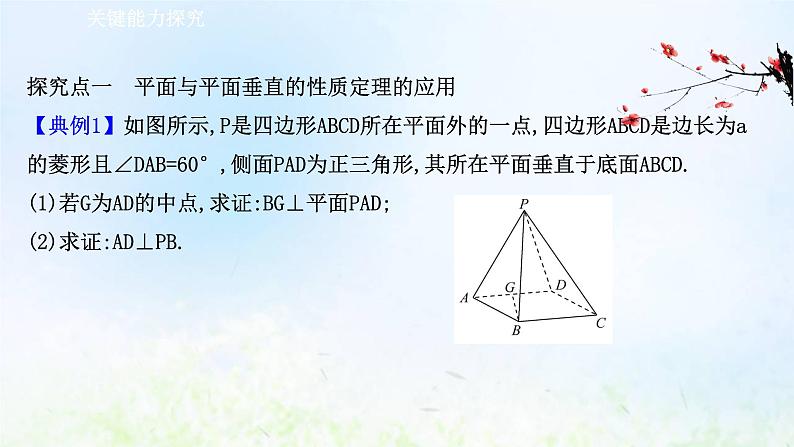
探究点一　平面与平面垂直的性质定理的应用【典例1】如图所示,P是四边形ABCD所在平面外的一点,四边形ABCD是边长为a的菱形且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD.(1)若G为AD的中点,求证:BG⊥平面PAD;(2)求证:AD⊥PB.
【思维导引】(1)连接BD,菱形ABCD,∠DAB=60° △ABD为正三角形 BG⊥AD 由平面与平面垂直的性质定理得出结论(2)连接PG,要证AD⊥PB,只需证AD⊥平面PBG即可.
【证明】(1)如图,在菱形ABCD中,连接BD,因为∠DAB=60°,所以△ABD为正三角形,因为G是AD的中点,所以BG⊥AD.因为平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,所以BG⊥平面PAD.
(2)如图,连接PG.因为△PAD是正三角形,G是AD的中点,所以PG⊥AD,由(1)知BG⊥AD.又因为PG∩BG=G.所以AD⊥平面PBG.而PB⊂平面PBG,所以AD⊥PB.
【类题通法】面面垂直性质定理的应用技巧　(1)面面垂直的性质定理,为线面垂直的判定提供了依据和方法.所以当已知两个平面垂直的时候,经常找交线的垂线,这样就可利用面面垂直证明线面垂直.(2)两平面垂直的性质定理告诉我们要将面面垂直转化为线面垂直,方法是在其中一个面内作(找)与交线垂直的直线.
【定向训练】1.(2019·全国卷Ⅲ)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则(　　) A.BM=EN,且直线BM,EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM,EN是异面直线D.BM≠EN,且直线BM,EN是异面直线
【解析】选B.因为直线BM,EN都是平面BED内的直线,且不平行,即直线BM,EN是相交直线.设正方形ABCD的边长为2a,则由题意可得:DE=2a,DM=a,DN= a,DB=2 a,根据余弦定理可得:BM2=DB2+DM2-2DB·DMcs∠BDE=9a2-4 ·a2cs∠BDE,EN2=DE2+DN2-2DE·DNcs∠BDE=6a2-4 a2cs∠BDE,所以BM≠EN.
2.如图所示,四棱锥V-ABCD的底面是矩形,侧面VAB⊥底面ABCD,又VB⊥平面VAD.求证:平面VBC⊥平面VAC.【证明】因为平面VAB⊥底面ABCD,且BC⊥AB.所以BC⊥平面VAB,所以BC⊥VA,又VB⊥平面VAD,所以VB⊥VA,又VB∩BC=B,所以VA⊥平面VBC,因为VA⊂平面VAC.所以平面VBC⊥平面VAC.
探究点二垂直关系的综合应用【典例2】如图,C是以AB为直径的圆O上异于A,B的点,平面PAC⊥平面ABC,E,F分别是PC,PB的中点,记平面AEF与平面ABC的交线为l.(1)求证:平面PBC⊥平面PAC.(2)求证:直线l⊥AC.【思维导引】(1)关键是利用圆的性质,推出BC⊥AC,再利用面面垂直推出线面垂直.(2)关键是先确定与直线l平行的直线,再证明垂直.
【证明】(1)因为AB是☉O的直径,所以AB所对的圆周角∠ACB=90°,所以AC⊥CB,又因为平面PAC⊥平面ABC,且平面PAC∩平面ABC=AC,BC⊂平面ABC,所以BC⊥平面PAC,又因为BC⊂平面PBC,所以平面PBC⊥平面PAC.(2)因为E,F分别为PC,PB的中点,所以EF为△PCB的中位线,所以EF∥BC,又因为EF⊄平面ACB,BC⊂平面ACB,所以EF∥平面ABC,又因为EF⊂平面AEF,且平面AEF∩平面ABC=l,所以EF∥l,故l∥BC,由(1)知,BC⊥AC,所以l⊥AC.
【类题通法】1.线面垂直条件的应用技巧当题目条件中含有线面垂直的条件时,一般想到的结论为:(1)线线垂直,即直线与平面内任一直线垂直.(2)面面垂直,即经过该直线的平面与该平面垂直.
2.面面垂直条件的应用技巧当题目中含有面面垂直的条件时,一般想到的解题思路为:(1)可以在一个平面内找或作一条垂直于交线的直线,转化为线面垂直,进而转化为线线垂直.(2)求斜线与某一平面所成的角,观察该斜线是否与另一平面相交,若相交可过交点在该平面内作交线的垂线,进而找到斜线的射影.(3)求点到平面的距离,可转化为某一平面内一点到交线的距离.
【知识延拓】如图,在三棱锥A -BCD中,AB⊥AD, BC⊥BD, 平面ABD⊥平面BCD, 点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.求证:(1)EF∥平面ABC.(2)AD⊥AC.【解题指南】(1)根据AB⊥AD,EF⊥AD,可得EF∥AB,从而得EF∥平面ABC.(2)证明BC⊥AD,再由AB⊥AD,从而可得AD⊥平面ABC,即得AD⊥AC.
【证明】(1)在平面ABD内,因为AB⊥AD,EF⊥AD,所以EF∥AB.又因为EF⊄平面ABC,AB⊂平面ABC,所以EF∥平面ABC.(2)因为平面ABD⊥平面BCD,平面ABD∩平面BCD=BD, BC⊂平面BCD,BC⊥BD,所以BC⊥平面ABD.因为AD⊂平面ABD,所以BC⊥AD.又因为AB⊥AD,BC∩AB=B,AB⊂平面ABC,BC⊂平面ABC,所以AD⊥平面ABC,又因为AC⊂平面ABC,所以AD⊥AC.
【定向训练】　(2018·北京高考)如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,E,F分别为AD,PB的中点.(1)求证:PE⊥BC;(2)求证:平面PAB⊥平面PCD;(3)求证:EF∥平面PCD.
【证明】(1)在△PAD中,PA=PD,E是AD的中点,所以PE⊥AD,又底面ABCD为矩形,所以AD∥BC,所以PE⊥BC.
(2)因为底面ABCD为矩形,所以AD⊥CD,又因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,CD⊂平面ABCD,所以CD⊥平面PAD,又PA⊂平面PAD,所以CD⊥PA,又因为PA⊥PD,CD,PD⊂平面PCD,CD∩PD=D,所以PA⊥平面PCD,又PA⊂平面PAB,所以平面PAB⊥平面PCD.
(3)取PC的中点G,连接DG,FG, 因为底面ABCD为矩形,所以AD? BC,又E是AD的中点,所以DE? BC,在△PBC中,因为F,G分别是PB,PC的中点,所以FG? BC,所以DE? FG,四边形DEFG是平行四边形,所以EF∥DG,又因为EF⊄平面PCD,DG⊂平面PCD,所以EF∥平面PCD.
【补偿训练】1.在平面四边形ABCD中,已知AB=BC=CD=a,∠ABC=90°,∠BCD=135°,沿AC将四边形折成直二面角B-AC -D.(1)求证:平面ABC⊥平面BCD.(2)求平面ABD与平面ACD所成的角的度数.【解题指南】(1)由二面角B-AC -D为直二面角,得CD⊥平面ABC,从而得平面BCD⊥平面ABC.(2)作BE⊥AC,EF⊥AD,连接BF,可证∠BFE即为二面角B?AD?C的平面角.解△BEF即可.
【解析】(1)在四边形ABCD中,因为AB=BC,AB⊥BC,所以∠ACB=45°,而∠BCD=∠ACB+∠ACD=135°,所以∠ACD=90°,即CD⊥AC.又平面ABC与平面ACD的二面角的平面角为直角,且平面ABC∩平面ACD=AC,所以CD⊥平面ABC,又CD⊂平面BCD,所以平面ABC⊥平面BCD.
(2)过点B作BE⊥AC,E为垂足,则BE⊥平面ACD.又过点E在平面ACD内作EF⊥AD,F为垂足,连接BF.由已知可得BF⊥AD,所以∠BFE是二面角B-AD-C的平面角.
因为E为AC的中点,所以AE= AC= a.又sin∠DAC= 所以EF= AE,所以EF= a· = a,tan∠BFE= 所以∠BFE=60°,即平面ABD与平面ACD所成的角的度数为60°.
2.如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面BAC,D,E分别为AB,AC的中点.(1)求证:AB⊥PE.(2)求二面角A-PB-E的大小.
【解析】(1)连接PD,因为PA=PB,D为AB的中点,所以PD⊥AB.因为DE∥BC,BC⊥AB,所以DE⊥AB.又因为PD∩DE=D,所以AB⊥平面PDE,因为PE⊂平面PDE,所以AB⊥PE.　(2)因为平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,PD⊥AB,所以PD⊥平面ABC.则DE⊥PD,又ED⊥AB,PD∩AB=D,所以DE⊥平面PAB,过D作DF垂直PB于F,连接EF,则EF⊥PB,∠DFE为所求二面角的平面角,则DE= ,DF= ,则tan∠DFE= 故二面角A-PB-E的大小为60°.
1.下列说法错误的是(　　)A.若直线a∥平面α,直线b∥平面α,则直线a不一定平行于直线bB.若平面α不垂直于平面β,则α内一定不存在直线垂直于平面βC.若平面α⊥平面β,则α内一定不存在直线平行于平面βD.若平面α⊥平面υ,平面β⊥平面υ,α∩β=l,则l一定垂直于平面υ【解析】选C.C错误,平面α⊥平面β,在平面α内,平行于α,β交线的直线和平面β平行.
2.若平面α⊥平面β,平面β⊥平面γ,则(　　)A.α∥γ　　　　　B.α⊥γC.α与γ相交但不垂直　　　D.以上都有可能【解析】选D.可能平行,垂直,也可能相交.
3.已知平面α、β和直线m、l,则下列命题中正确的是(　　)A.若α⊥β,α∩β=m,l⊥m,则l⊥βB.若α∩β=m,l⊂α,l⊥m,则l⊥βC.若α⊥β,l⊂α,则l⊥βD.若α⊥β,α∩β=m,l⊂α,l⊥m,则l⊥β【解析】选D.选项A缺少了条件l⊂α;选项B缺少了条件α⊥β;选项C缺少了条件α∩β=m,l⊥m;选项D具备了面面垂直的性质定理的全部条件.
4.如图,在斜三棱柱ABC -A1B1C1中,∠BAC=90°,BC1⊥AC,则C1在底面ABC上的射影H必在(　　)A.直线AB上B.直线BC上C.直线AC上D.△ABC内部【解析】选A.连接AC1,因为AC⊥AB,AC⊥BC1,所以AC⊥平面ABC1.又AC⊂平面ABC,所以平面ABC1⊥平面ABC,所以C1在平面ABC上的射影H必在平面ABC1与平面ABC的交线AB上.