11.3. 多边形及其内角和课件PPT

这是一份11.3. 多边形及其内角和课件PPT，共24页。

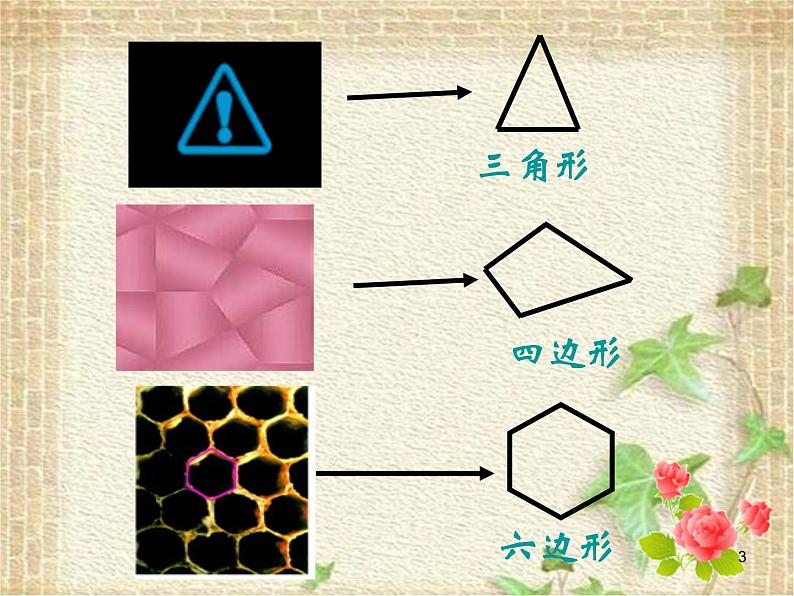
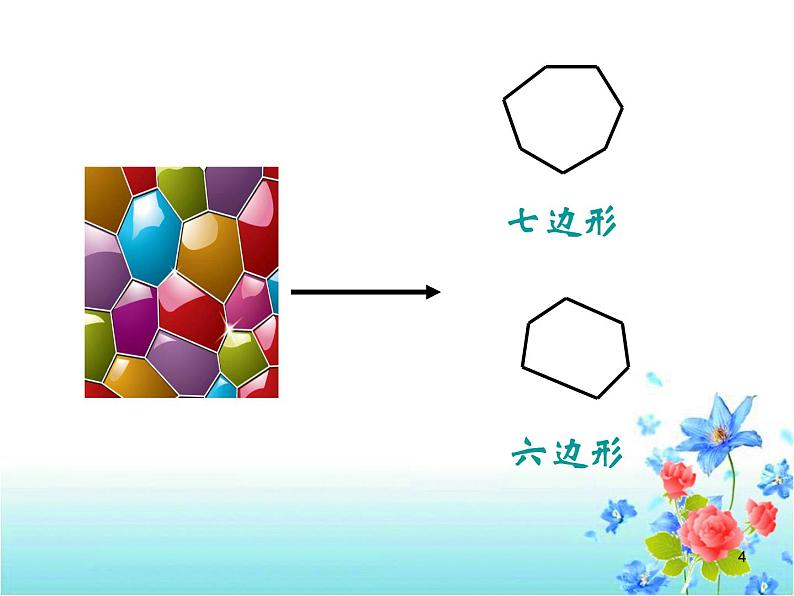
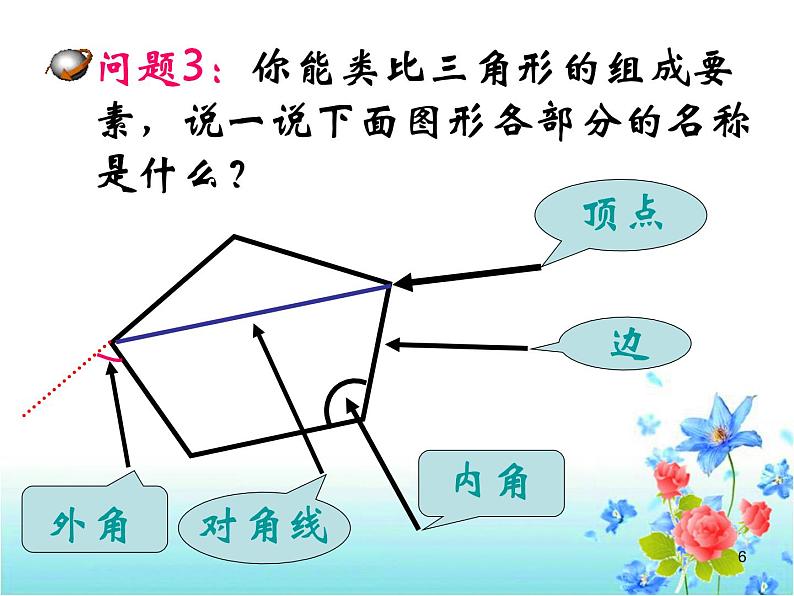
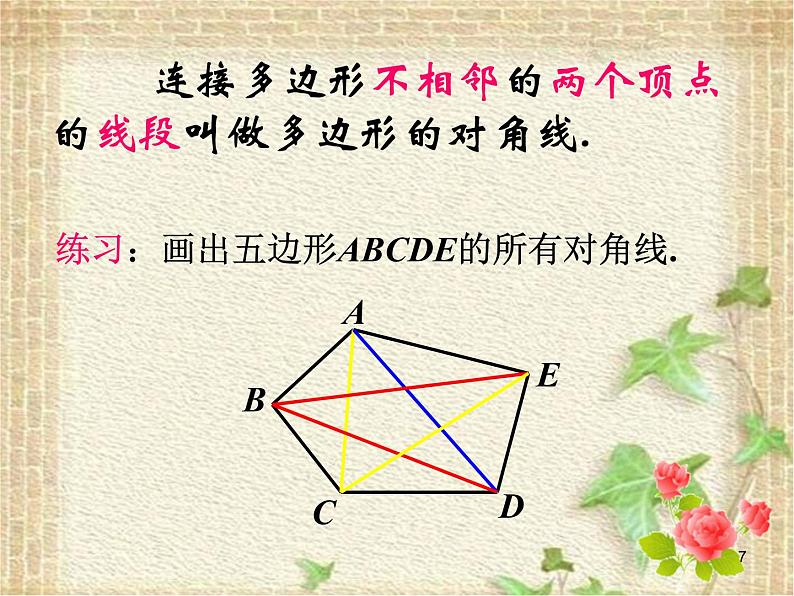
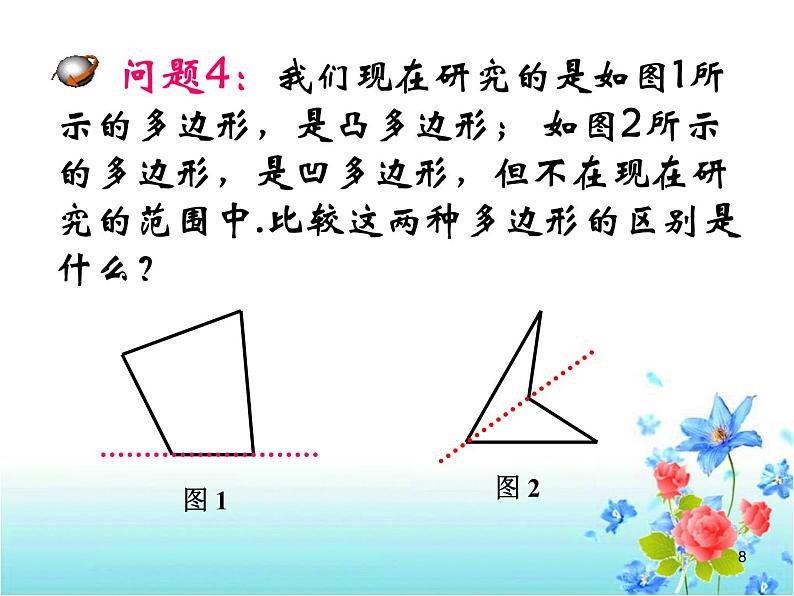
11.3.1 多边形1问题1：你能从这些图形中找出几个由一些线段围成的平面图形吗？2三角形 四边形 六边形 3 七边形 六边形4 类比三角形的定义，你能说出什么叫四边形、五边形、多边形吗？ 由不在同一直线上的 线段首尾顺次相接组成的图形叫做 边形.五四条问题2：思考：关于多边形的定义是否正确？5问题3：你能类比三角形的组成要素，说一说下面图形各部分的名称是什么？ 边内角顶点对角线6练习：画出五边形ABCDE的所有对角线. 连接多边形不相邻的两个顶点的线段叫做多边形的对角线. 7 问题4：我们现在研究的是如图1所示的多边形，是凸多边形； 如图2所示的多边形，是凹多边形，但不在现在研究的范围中.比较这两种多边形的区别是什么？8问题5：观察正三角形、正方形的特征， 猜想满足什么条件的多边形是正多边形？定义： 如果多边形的各边都相等，各内角也都相等，那么就称它为正多边形.9 例 你知道三角形、四边形、五边形、六边形等多边形从一个顶点出发所画的对角线的条数吗？试着画一画，并填下表：      n－301231234n－2025910练习测试 2、（1）一个多边形自一个顶点出发的对角线把它分成6个三角形，则它是＿＿边形.   1、 课本81页练习第1、2题. （2）下列图形哪些是凸多边形，哪些不是？11今天的收获 2、多边形为什么研究对角线？ 你对多边形的对角线有哪些认识？   1、 谈谈本节课你学会哪些知识？ 3、你还有哪些疑问和困惑？12第1题 作业： 13 问题1 我们学校要建一个边长都是6 米，各角都相等的十边形的大花坛，请同学们一起来 设计图纸．14 【问题2】 三角形的内角和等于180°，正方形的内角和等于360°，那么任意四边形的内角和是否也等于360°呢？证明你的结论．ABCD结论：四边形的内角和等于360°. 15 【问题3】类比四边形内角和的推导方法，你能求五边形、六边形……n边形的内角和各是多少吗？  1 2 3 4n－21800360054007200(n－2)×180016总结：探索多边形的内角和关键是 把多边形分成几个三角形，再利用三角形的内角和求得.n×180o－360o（n－1）×180o－180o思考：把一个多边形分成几个三角形， 还有其他分法吗？ 17例1 如果一个四边形的一组对角互补，那么另一组对角有什么关系？ABCD解：四边形ABCD中， ∠A+∠C=180°.∵∠A+∠B+∠C+∠D=360°，∴∠B+∠D=360°－(∠A+∠C ) =360°－180°=180°.结论：如果四边形的一组对角互 补，那么另一组对角也互补.18例2 如图，在六边形的每个顶点处各取一个外角，这些外角的和叫做六边形的外角和．六边形的外角和等于多少？分析：（1）回忆三角形的外角和的求法；（2）任何一个外角同与它相邻的内角有什么关系？（3）六边形的6个外角加上与它们相邻的内角，所得总和是多少？（4）上述总和与六边形的内角和、外角和有什么关系？19例3 三角形、六边形的外角和都是360°，那么n边形的外角和（n是不小于3的任意整数）还是360°吗？若是，证明你的结论；若不是，请说明你的理由．结论：多边形的外角和等于360°归纳：多边形的外角和的推导方法 多边形的内角和+外角和=边数×180°201．练习1、2、3题.2．一个多边形的内角和是外角和的3倍，它是几边形？解：设这个多边形的边数为n， 根据题意，得（n－2）×180=3×360.解这个方程，得n= 8 . 答：这个多边形是八边形.感悟：方程思想解决几何问题的优越性21（1）十二边形的内角和是 ，外角和是 ．（2）一个多边形的每个内角都是160°，这是几边形？ 1800o360o解：设这个多边形的边数为n， 根据题意，得（n－2）×180=160n.解这个方程，得 n = 18. 答：这个多边形是十八边形.思考：还有其他解法吗？比较两种解法， 哪个更好？22今天的收获 1、n边形的内角和等于（n－2）×180°.    3、利用类比归纳、转化的学习方法，可以把多边形问题转化为三角形问题来解决; 外角问题转化为内角来解决. 4、方程的数学思想在几何中有重要的作用. 【问题4】本节课你学会哪些知识？学会了哪些解决问题的方法？你还有哪些疑问？ 2、n边形的外角和等于360°. 23第2、3、4、5、6题.已知一个多边形除了一个内角外，其余各内角的和是2750°，求这个多边形的边数. 作业24