2021学年27.3 位似教学ppt课件

这是一份2021学年27.3 位似教学ppt课件，共27页。PPT课件主要包含了导入新课，探究新知一，知识归纳一，典型例题一，当堂训练一，位似图形的性质，探究新知二，当堂训练二，课堂小结，补充练习等内容，欢迎下载使用。

1.如何判断两个图形是不是位似图形?
一、这两个图形是相似的,对应边互相平行；二、每组对应点所在的直线都经过同一点。
2.位似图形的一般步骤有哪些？
①确定位似中心；②分别连接并延长位似中心和能代表原图的关键点；③根据相似比,确定能代表所作的位似图形的关键点；④顺次连接上述各点,得到放大或缩小的图形.
我们知道,在直角坐标系中,可以利用变化前后两个多边形对应顶点的坐标之间的关系表示某些平移、轴对称和旋转(中心对称).那么,位似是否也可以用两个图形坐标之间的关系来表示呢？
平面直角坐标系中的位似变换
平面直角坐标系中的图形变换
如图,把AB缩小后A,B的对应点为 A´( ， )， B´( ， )； A" ( , )， B" ( , ).
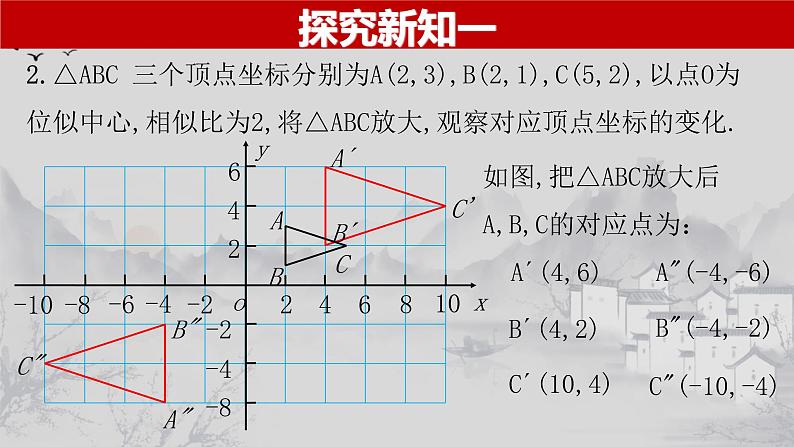
2.△ABC 三个顶点坐标分别为A(2,3),B(2,1),C(5,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化.
如图,把△ABC放大后A,B,C的对应点为：
【问题1】在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作几个?【问题2】所作位似图形与原图形在原点的同侧,那么对应顶点的坐标的比与其相似比是何关系?如果所作位似图形与原图形在原点的异侧呢?
1.在平面直角坐标系中,以原点为位似中心作一个图形的位似图形可以作两个．2.当位似图形在原点同侧时,其对应顶点的坐标的比为k； 当位似图形在原点两侧时,其对应顶点的坐标的比为-k．3.当k＞1时,图形扩大为原来的k倍； 当0＜k＜1时,图形缩小为原来的 ．
【例1】如图,在平面直角坐标系中,△ABO三个顶点的坐标分别为A(-2,4),B(-2,0),O(0,0).以原点O为位似中心,画出一个三角形使它与△ABO的相似比为3:2.
解：利用位似中对应点的坐标的变化规律,分别取点A´(-3,6),B´(-3,0),O(0,0).
1.如图,线段AB两个端点的坐标分别为A(4,4),B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的1/2后得到线段CD,则端点D的坐标为( ) A.(2，2) B.(2，1) C.(3，2) D.(3，1)
3.在平面直角坐标系中,四边形OABC的顶点坐标分别为O(0,0)，A(6,0)，B(3,6),C(-3,3).以原点O为位似中心,画出四边形OABC的位似图形,使它与四边形OABC的相似是2:3.
检测自学效果一(复述概念)(3分钟)
【探究2】(1)如图,在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为1:3,把线段AB缩小.观察对应点之间坐标的变化,你有什么发现?
(2)如图,△ABC三个顶点坐标分别为A(2,4),O(0,0),C(5,0),以点O为位似中心,相似比为2,将△AOC放大,观察对应顶点坐标的变化,你有什么发现？
以坐标原点为位似中心的位似变换有以下性质：若原图形上点的坐标为(x,y),与原图形的位似比为k,则对应的位似图形上的点的坐标为:(kx,ky)或(-kx,-ky)。
检测自学效果二(复述例题)(6分钟)
【例】如图,△ABO 的三个顶点的坐标分别为A(-2,4),B(-2,0),O(0,0).以原点O为位似中心,画出一个三角形,使它与△ABO的相似比为3:2．
当堂训练1(解题规范、争取满分)(4分钟)
1.如图,在正方形ABCD、OEFG中,点D和F的坐标分别为(-3,2)和(1,-1),则这两个正方形的位似中心的坐标为___________.
(-1,0)或(5,-2)
2.如图,在△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A´B´C´,并把△ABC的边长放大到原来的2倍.设点B的对应点B´的横坐标是a,求点B的横坐标．
至此,我们已经学习了四种变换：平移、轴对称、旋转和位似,你能说出它们之间的异同吗？在右图所示的图案中,你能找到这些变换吗？
将图中的△ABC做下列变换,画出相应的图形,指出三个顶点的坐标所发生的变化. (1)沿y轴正向平移3个单位长度； (2)关于x轴对称； (3)以C为位似中心,将△ABC放大2倍； (4)以C为中心,将△ABC顺时针旋转180º.
平面直角坐标系中的位似
平面直角坐标系中的位似图形的画法
1.将平面直角坐标系中某个图形的各点坐标做如下变化,其中属于位似变换的( ) A.将各点的纵坐标乘以2,横坐标不变； B.将各点的横坐标除以2,纵坐标不变； C.将各点的横坐标、纵坐标都乘以2； D.将各点的纵坐标减去2,横坐标加上2。
2.如图,小朋在坐标系中以A为位似中心画了两个位似的直角三角形,可不小心把E点弄脏了,则E点坐标为( ) A.(4,-3) B.(4,-2) C.(4,-4) D.(4,-6)
3.原点O是△ABC和△A´B´C´的位似中心,点A(1,0)与点A´(-2,0) 是对应点,△ABC的面积是1.5,则△A´B´C´的面积是 .