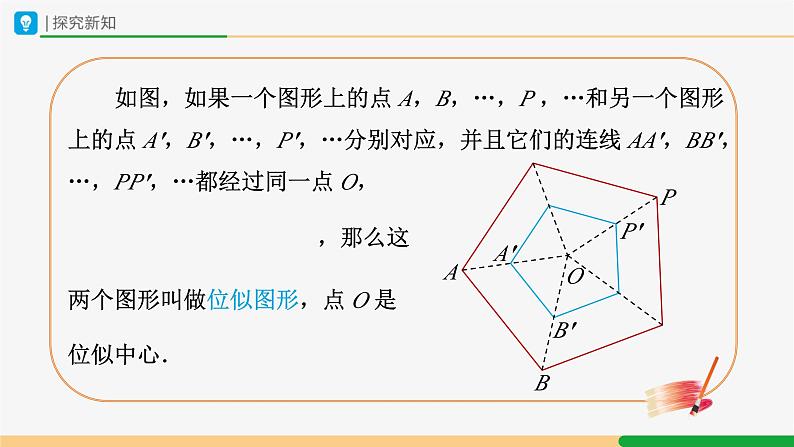












初中数学人教版九年级下册第二十七章 相似27.3 位似优质ppt课件
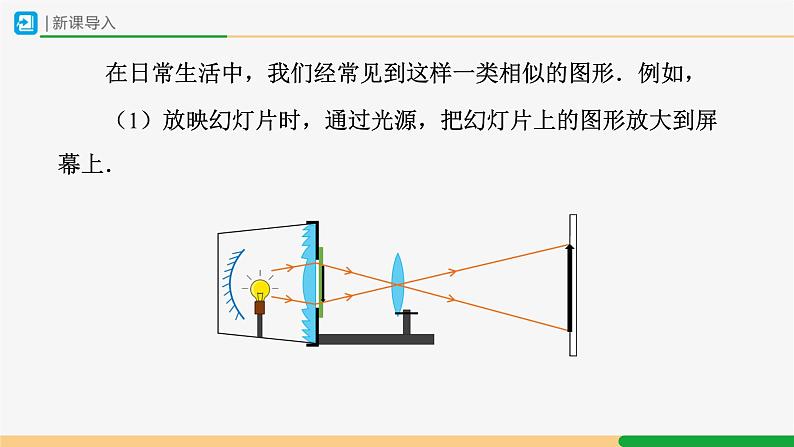
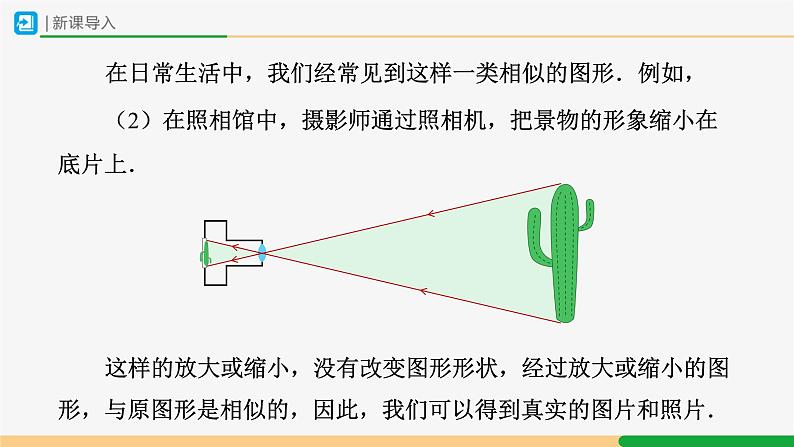
展开在日常生活中,我们经常见到这样一类相似的图形.例如,
(1)放映幻灯片时,通过光源,把幻灯片上的图形放大到屏幕上.
(2)在照相馆中,摄影师通过照相机,把景物的形象缩小在底片上.
这样的放大或缩小,没有改变图形形状,经过放大或缩小的图形,与原图形是相似的,因此,我们可以得到真实的图片和照片.
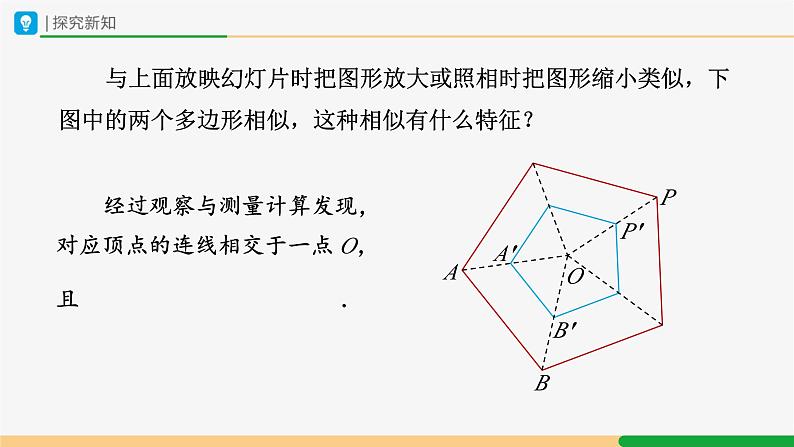
与上面放映幻灯片时把图形放大或照相时把图形缩小类似,下图中的两个多边形相似,这种相似有什么特征?
位似图形与相似图形有什么区别呢?
(1)相似只要求两个图形的形状完全相同,而位似不仅要求图形相似,还必须有特殊的位置关系,即对应顶点的连线相交于同一点.(2)如果两个图形是位似图形,那么这两个图形必是相似图形,但相似的两个图形不一定是位似图形.
对于两个多边形,如果它们的对应顶点的连线相交于一点,并且这点与对应顶点所连线段成比例,那么这两个多边形就是位似多边形.
类比位似图形的概念,你能给出位似多边形的概念吗?
本节课下面所讲的位似图形只包括位似多边形.
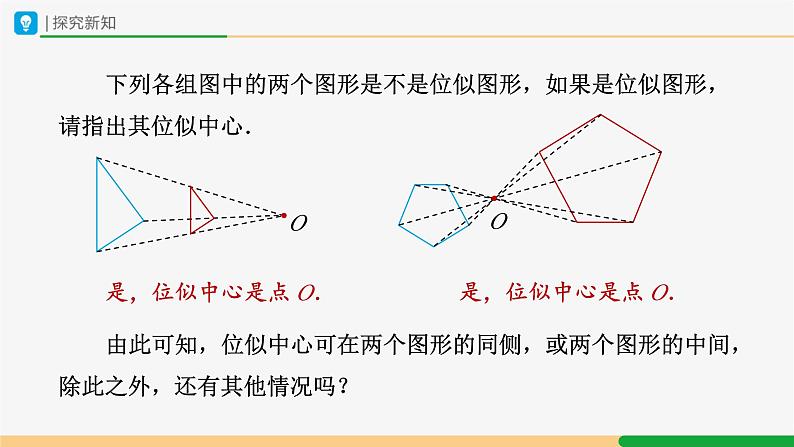
下列各组图中的两个图形是不是位似图形,如果是位似图形,请指出其位似中心.
是,位似中心是点 O.
由此可知,位似中心可在两个图形的同侧,或两个图形的中间,除此之外,还有其他情况吗?
位似图形有哪些性质呢?
(1)位似图形是相似图形,那么位似图形有相似图形的性质,即对应角相等,对应边成比例.
(2)根据定义,位似图形的所有对应点的连线相交于一点,这个点就是位似中心.
(3)根据定义,位似中心与对应顶点(在不重合的情况下)所连线段成比例.
那么这个比是多少呢?
根据相似三角形的判定和性质可知,位似图形上任意一对对应点(到位似中心的距离为 0 的点除外)到位似中心的距离之比等于相似比.
(4)位似图形的对应边有什么位置关系吗?
位似图形的对应边互相平行(根据相似三角形的性质和平行线的判定可知),或在同一条直线上.
如何利用位似将一个图形放大或缩小呢?
②分别在线段 OA,OB,OC,OD 上取点 A′,B′,C′,D′,使得 .
③顺次连接点 A′,B′,C′,D′,所得四边形 A′B′C′D′ 就是所要求的图形.
例如,把四边形 ABCD 缩小到原来的 .
①如图,在四边形外任选一点 O.
如果在四边形外任选一个点 O,分别在 OA,OB,OC,OD 的反向延长线上取 A′,B′,C′,D′,使得 呢?尝试画出四边形 A′B′C′D′.
如果点 O 取在四边形 ABCD 内部呢?尝试画出四边形 A′B′C′D′.
画位似图形的一般步骤1.确定位似中心并找出原图形的关键点.2.分别连接位似中心和原图形的关键点.3.根据相似比,在位似中心与各关键点所确定的直线上取点,确定所画位似图形的关键点的位置.4.顺次连接所作各点,得到放大或缩小的图形.
例1 如图,以点 O 为位似中心,将△ABC 放大为原来的 2 倍.
解:①作射线 OA,OB,OC.
②分别在线段 OA,OB,OC 上取点 A′,B′,C′,使得 .
③顺次连结接A′,B′,C′,△A′B′C′ 就是所要求图形.
例2 下列图形中△ABC∽△DEF,但这两个三角形不是位似图形的是( ).
解析:观察对应点的连线是否交于一点,若交于一点,则是位似图形;否则,不是位似图形.
位似图形必须同时满足的两个条件1.两个图形是相似图形;2.两个相似图形的对应顶点的连线相交于同一点.
对应角相等,对应边成比例
对应点的连线相交于一点
位似图形上任意一对对应点(到位似中心的距离为 0 的点除外)到位似中心的距离之比等于相似比
对应边互相平行或在同一条直线上
初中数学人教版九年级下册27.3 位似优质课件ppt: 这是一份初中数学人教版九年级下册27.3 位似优质课件ppt,文件包含273教学课件位似第2课时pptx、273教学设计位似第2课时docx、273预习导学位似第2课时docx、273练习·基础巩固位似第2课时docx、273练习·能力提升位似第2课时docx、273练习·素能拓展位似第2课时docx等6份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
数学九年级下册27.3 位似完整版课件ppt: 这是一份数学九年级下册27.3 位似完整版课件ppt,文件包含273教学课件位似第3课时pptx、273教学设计位似第3课时docx、273预习导学位似第3课时docx、273练习·基础巩固位似第3课时docx、273练习·能力提升位似第3课时docx、273练习·素能拓展位似第3课时docx等6份课件配套教学资源,其中PPT共21页, 欢迎下载使用。
人教版九年级下册第二十七章 相似27.3 位似试讲课课件ppt: 这是一份人教版九年级下册第二十七章 相似27.3 位似试讲课课件ppt,文件包含273位似第2课时平面直角坐标系中的位似pptx、273位似第2课时平面直角坐标系中的位似教案doc、273位似第2课时平面直角坐标系中的位似导学案doc等3份课件配套教学资源,其中PPT共34页, 欢迎下载使用。