数学九年级下册27.3 位似课文配套ppt课件

这是一份数学九年级下册27.3 位似课文配套ppt课件，共26页。PPT课件主要包含了位似中心，2-3，-2-3，-kx，-ky等内容，欢迎下载使用。

1.理解平面直角坐标系中，位似图形对应点的坐标之间的联系．2.会用图形的坐标的变化表示图形的位似变换，掌握把一个图形按一定比例放大或缩小后，点的坐标变化的规律. (重点、难点)3.了解四种图形变换 (平移、轴对称、旋转和位似) 的异同，并能在复杂图形中找出这些变换.
1.如图，若AB∥CD，则△OAB___△OCD，△OAB与△OCD是_____图形，点O是它们的_________；  2.在平面直角坐标系中，若点A的坐标为(2，3)，则点A关于x轴对称的点的坐标是_______，关于y轴对称的点的坐标是_______，关于原点对称的点的坐标是________.
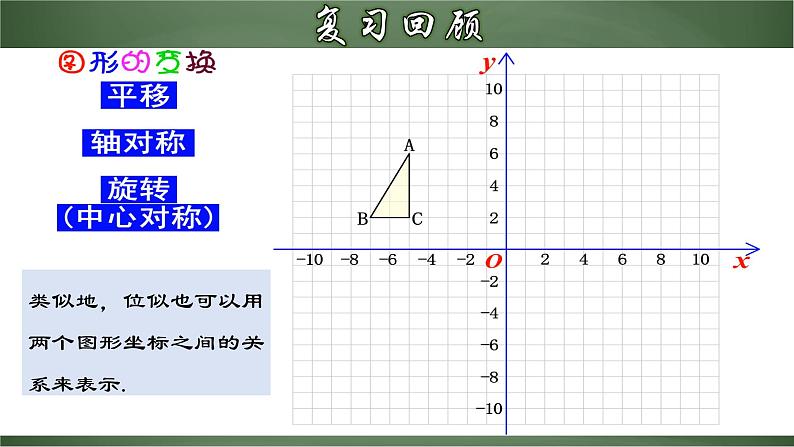
类似地，位似也可以用两个图形坐标之间的关系来表示.
A'(___，___)，B'(___，___)；A″(___，___)，B″(___，___).
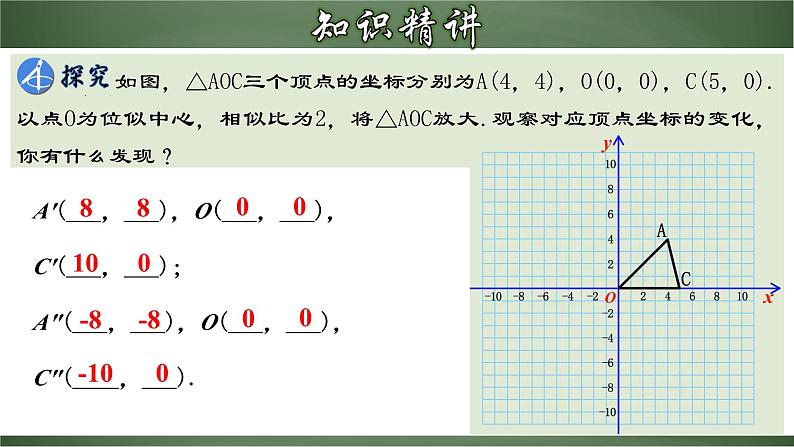
如图，△AOC三个顶点的坐标分别为A(4，4)，O(0，0)，C(5，0).以点O为位似中心，相似比为2，将△AOC放大.观察对应顶点坐标的变化，你有什么发现？
A'(___，___)，O(___，___)，C'(___，___)；A″(___，___)，O(___，___)，C″(____，___).
一般地，在平面直角坐标系中，如果以原点为位似中心，画出一个与原图形位似的图形，使它与原图形的相似比为k，那么与原图形上的点(x，y)对应的位似图形上的点的坐标为(___，___)或(____，____).
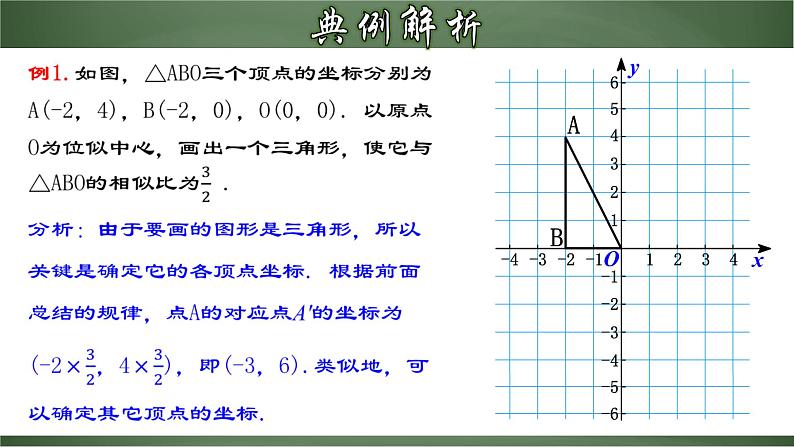
解：如图，利用位似中对应点的坐标的变化规律，分别取点A'(-3，6)，B' (-3，0)，O(0，0). 顺次连接A'，B'，O，所得△A'B'O就是要画的一个图形.
解：如图，利用位似中对应点的坐标的变化规律，分别取点A''(3，-6)，B'' (3，0)，O(0，0).顺次连接A''，B''，O，所得△A''B''O就是要画的一个图形.
在平面直角坐标系中，四边形OABC的顶点坐标分别为O(0，0)，A(6，0)，B (3，6)，C(－3，3). 以原点O为位似中心，画出四边形OABC的位似图形，使它与四边形OABC的相似是2:3.
例2.如图，在平面直角坐标系中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为1:3，点A，B，E在x轴上.(1)若点F的坐标为(4.5, 3),直接写出点A和点C的坐标;(2)若正方形BEFG的边长为6，求点C的坐标.
解:(2)∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，相似比是1:3，正方形BEFG的边长为6∴正方形ABCD的边长为2，OB:0E=1:3∴0B:(0B+6)=1:3,解得0B=3∴点C的坐标为(3，2)
1.如图，把△AOB缩小后得到的△COD，求△COD与△AOB的相似比.
解：依题意得，△COD∽△AOB.∵ B(5，0)，D(2，0)∴ OB=5，OD=2∴ OD:OB=2:5∴ △COD与△AOB的相似比为2:5.
2.如图，△ABO三个顶点的坐标分别为A(4，-5)，B(6，0)O(0，0).以原点O为位似中心，把这个三角形放大为原来的2倍，得到△A'B'O'.写出△A'B'O'三个顶的坐标.
解:利用位似中对应点的坐标的变化规律，分别得A'(8，-10) ,B'(12, 0),O' (0,0) ,或A'(-8,10),B'(-12,0)，O'(0,0).
3.将平面直角坐标系中某个图案的各点坐标作如下变化,其中属于位似变换的是( )A.将各点的纵坐标乘2,横坐标不变B.将各点的横坐标除以2，纵坐标不变C.将各点的横坐标、纵坐标都乘2D.将各点的纵坐标减去2，横坐标加上2 .
4.如图，在平面直角坐标系中，将△OAB以原点O为位似中心放大后得到△OCD，若B(0,1)，D(0，3),则△OAB与△OCD的相似比是( )A.2:1 B.1:2 C.3:1 D.1:3
7.在平面直角坐标系中，△ABC和△A1B1C1的相似比等于0.5，并且它们是关于原点O的位似图形，若点A的坐标为(2，4)，则其对应点A1的坐标是________________.8.如图，是△AOB和把它放大后得到的△COD，则△AOB与△COD的相似比为______.
(4，8)或(-4，-8)
9.如图，点A, B的坐标分别为(3,0)，(2,-3),△AB'O'是△AB0关于点A的位似图形，且点0'的坐标为(-1，0),则点B'的坐标为__________.
则:四边形A'B'C'D' 与A"B"C"D"为所要求的图形.
解:依题意得A' (-3,3)，B' (-4,1)，C' (-2,0)，D'(-1,2)；或A" (3，-3)，B"(4，-1)，C"(2,0)D"(1，-2).
11.在10×10的网格中建立如图所示的平面直角坐标系，已知格点A、B(两条网格线的交点叫格点).(1)将线段AB先向上平移4个单位长度，再向右平移1个单位长度，画出平移后的线段A1B1(A的对应点为A1,B的对应点为B1);
解:如图，线段A1B1即为所求;
11.在10×10的网格中建立如图所示的平面直角坐标系，已知格点A、B(两条网格线的交点叫格点).(2)以原点O为位似中心，画线段A2B2，使得A2B2与A1B1位似,且相似比为2:1 (A1的对应点为A2,B1的对应点为B2);
(3)连接AA2、BB2交于C点，则AC=_____.
解:如图，线段A2B2即为所求;