高中数学人教A版 (2019)必修 第一册1.2 集合间的基本关系教课ppt课件

这是一份高中数学人教A版 (2019)必修 第一册1.2 集合间的基本关系教课ppt课件，共17页。PPT课件主要包含了1相等集合，则AB，反之亦然，2真子集，Venn图为，重要结论，课堂练习等内容，欢迎下载使用。

观察下面几个例子，你能发现两个集合之间的关系吗？
⑴ A={1,2,3} , B={1,2,3,4,5};
⑵设A为来宾四中高一(2)班女生的全体组成的集合, B为这个班学生的全体组成的集合;
⑶ 设C＝{x|x是两条边相等的三角形}，D={x|x是等腰三角形}.
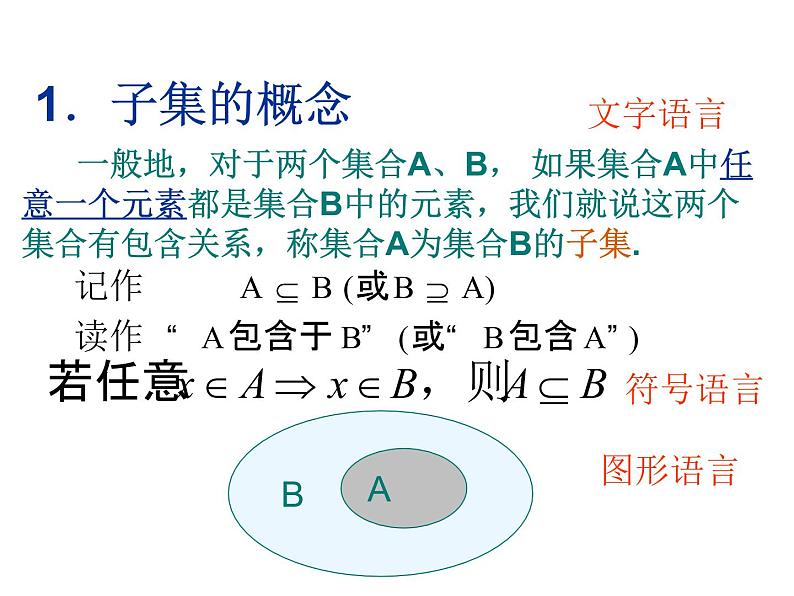
一般地，对于两个集合A、B， 如果集合A中任意一个元素都是集合B中的元素，我们就说这两个集合有包含关系，称集合A为集合B的子集.
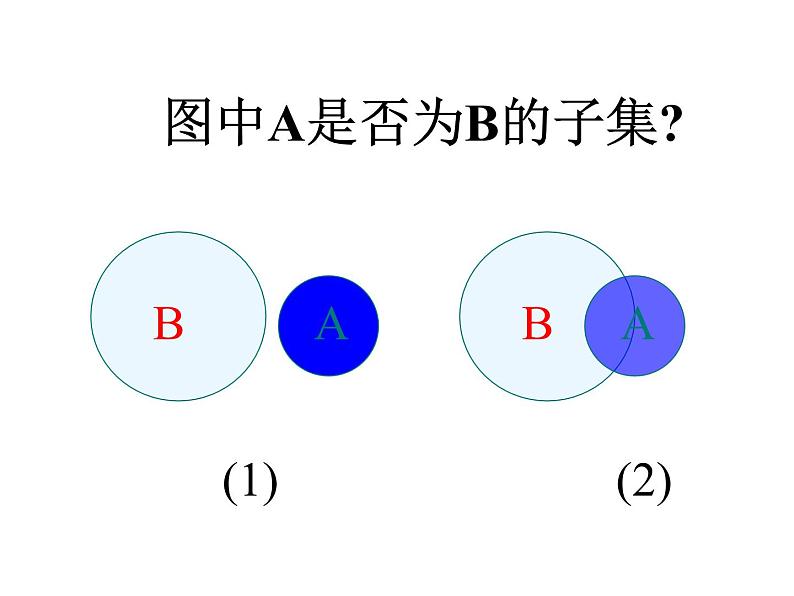
图中A是否为B的子集?
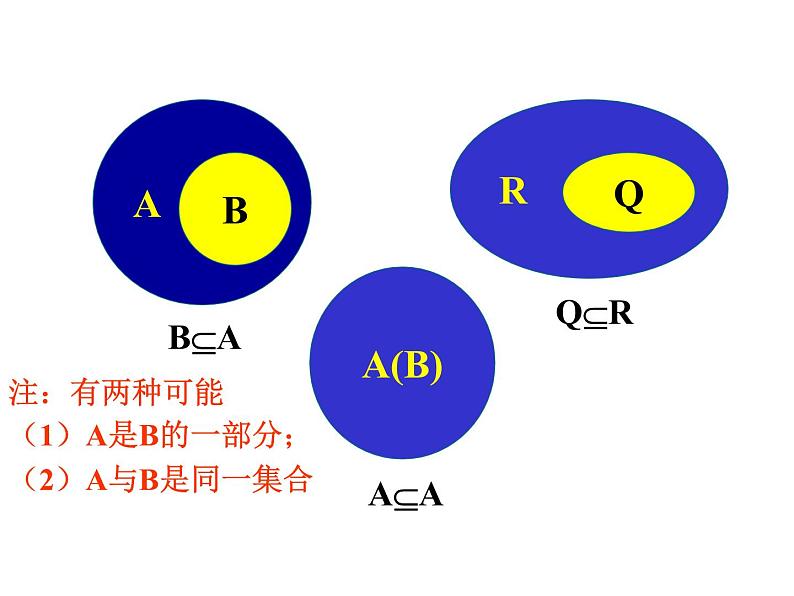
注：有两种可能（1）A是B的一部分；（2）A与B是同一集合
判断集合A是否为集合B的子集，若是则在（ ）打√，若不是则在（ ）打×: ①A={1,3,5}, B={1,2,3,4,5,6} ( ) ②A={1,3,5}, B={1,3,6,9} ( ) ③A={0}, B={x x2+2=0} ( ) ④A={a,b,c,d}, B={d,b,c,a} ( )
一般地,对于两个集合A与B, 如果集合A中的任何一个元素都是 集合B的元素,同时集合B中的任何一个元素都是集合A的元素,则称集合A等于集合B,记作
例A＝{ x|x是两边相等的三角形}，B＝{ x|x是等腰三角形}，有AB，BA，则A＝B
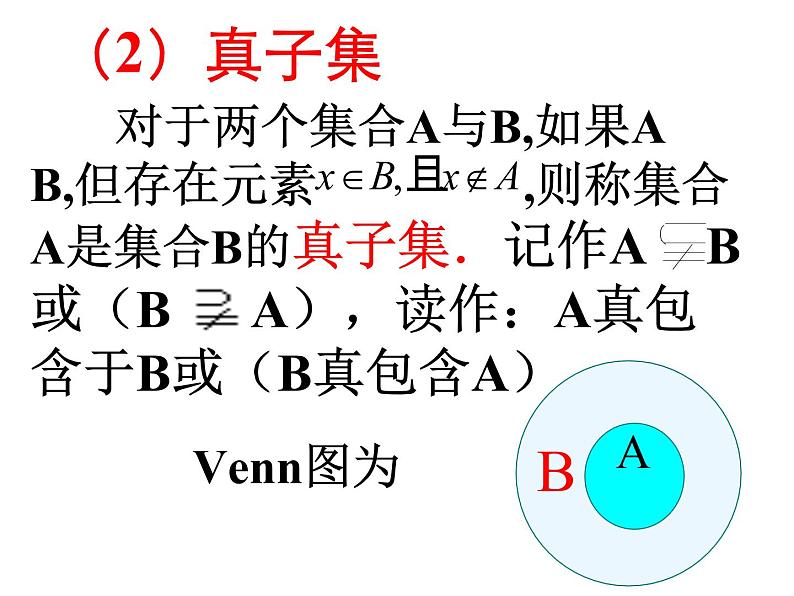
对于两个集合A与B,如果A B,但存在元素 ,则称集合A是集合B的真子集．记作A B或（B A），读作：A真包含于B或（B真包含A）
①空集是任何集合的子集Φ A ②空集是任何非空集合的真子集Φ A （A ≠ Φ） ③任何一个集合是本身的子集，即 A A ④对于集合A，B，C，如果 A B,且B C，则A C
⑤对于集合A, B, C,如果 A B, B C ,那 么A C ．
例1、在以下六个写法中①{0}∈{0，1} ②{0} ③{0，－1，1}{－1，0，1} ④⑤{}⑥{(0，0)}＝{0}.错误个数为 ( )
A.3个 B.4个 C.5个 D.6个
例2、⑴写出集合{a，b}的所有子集； ⑵写出所有{a，b，c}的所有子集； ⑶写出所有{a，b，c，d}的所有子集.
注意：一般地，集合A含有n个元素，则A的子集共有2n个，A的真子集共有2n－1个，非空真子集2n－2个.
解：⑴所有子集为，{a}，{b}，{a，b}；
⑵所有子集为，{a}，{b}，{c}，{a，b}，{a，b，c}， {a，c}，{b， c}；
⑶所有子集为，{a}，{b}，{c}，{d}，{a, b}，{b, c}，{a, d}，{a, c}， {b, d}， {c, d}， {a，b，c}，{a，b，d}， {b，c，d}， {a，d，c} {a，b，c，d}；
练习：已知A＝{x | x2－2x－3＝0}, B＝{x | ax－1＝0}, 若BA, 求实数a的值．
设集合A={x|1≤x≤3}，B={x|x-a≥0} 若A是B的真子集，求实数a的取值范围。