华师大版23.4 中位线课前预习ppt课件

这是一份华师大版23.4 中位线课前预习ppt课件，共18页。PPT课件主要包含了如何证明，针对练习，达标测评反思目标等内容，欢迎下载使用。

知识与能力1.理解三角形中位线定义与性质，2.会应用三角形中位线解决实际问题过程与方法经历探究三角形中位线定义、性质的过程，感受三角形中位线定理的应用思想情感态度与价值观培养良好的探究意识和合作交流的习惯，体会数学推理的应用价值
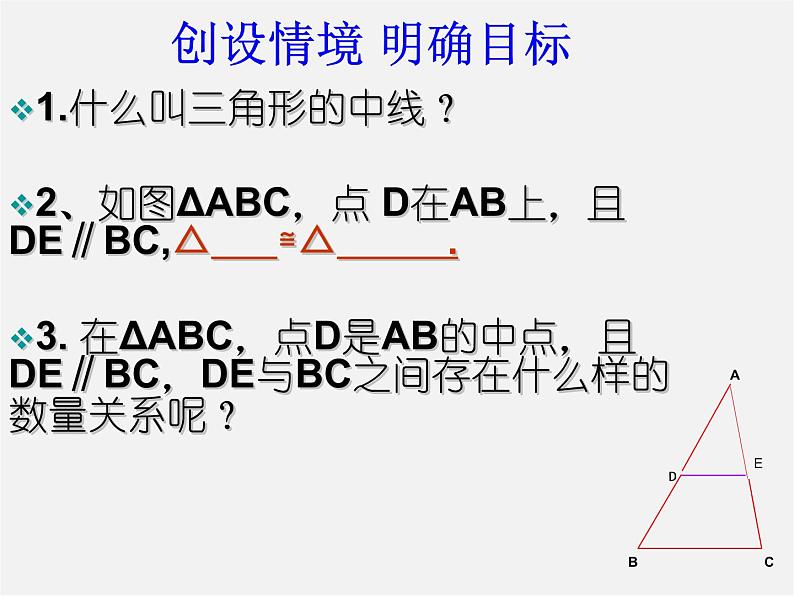
1.什么叫三角形的中线？2、如图ΔABC，点 D在AB上，且DE∥BC,△ ≌△ .3. 在ΔABC，点D是AB的中点，且DE∥BC，DE与BC之间存在什么样的数量关系呢？
图中线段DE 是连接ΔABC两边的中点D、E所得的线段，称此线段DE为ΔABC的中位线
三角形中位线的概念　
连接三角形两边的中点的线段叫做三角形的中位线
三角形的中位线与三角形的中线的区别是什么？　
答：三角形的中位线的两端都是中点 三角形的中线一端是中点，另一端是顶点
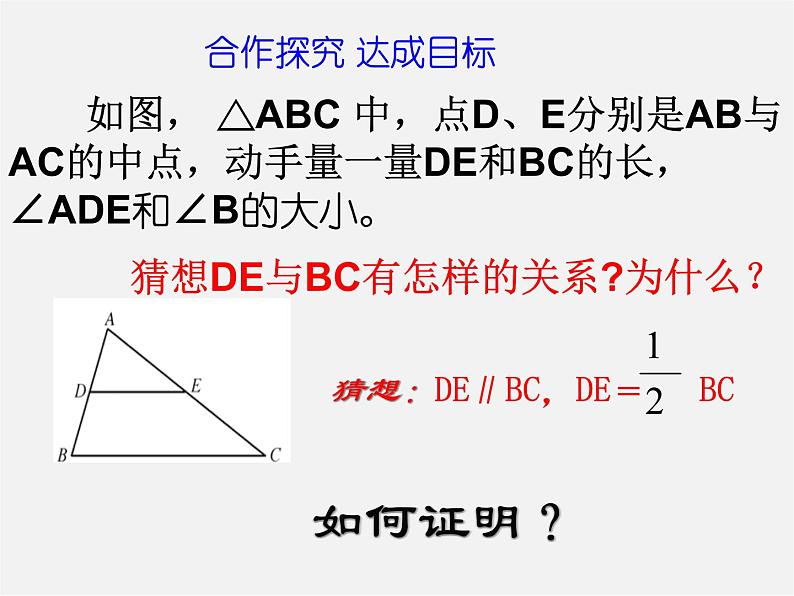
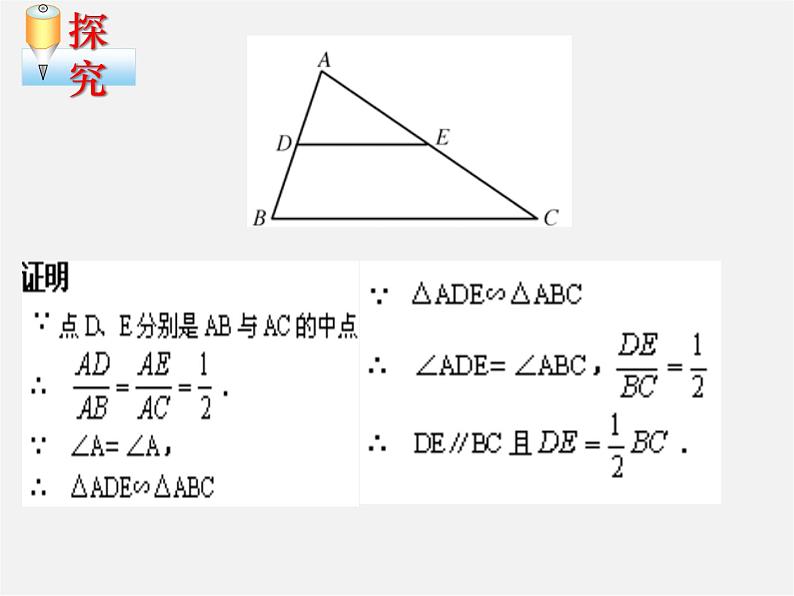
如图， △ABC 中，点D、E分别是AB与AC的中点，动手量一量DE和BC的长，∠ADE和∠B的大小。
猜想：DE∥BC，DE＝ BC
猜想DE与BC有怎样的关系?为什么？
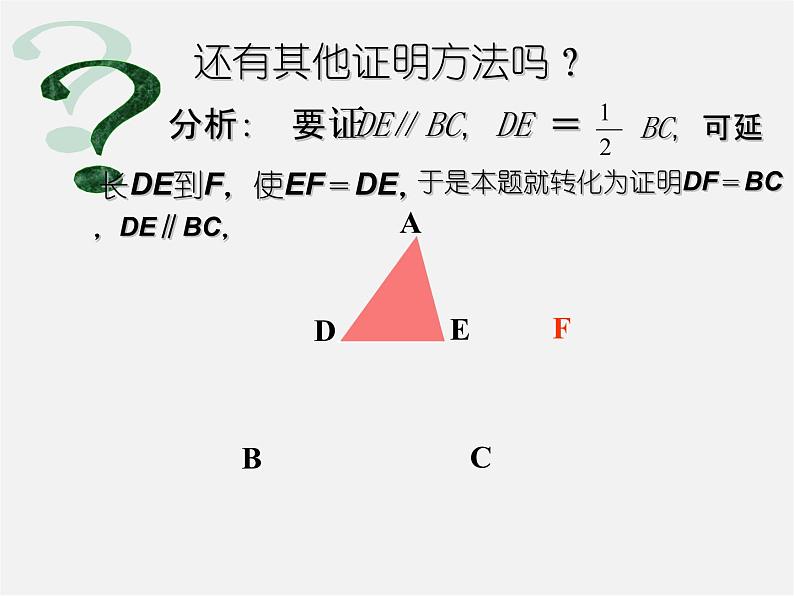
分析:　要证DE∥BC，DE ＝
长DE到F，使EF＝DE，
于是本题就转化为证明DF＝BC
三角形中位线的性质: 三角形的中位线平行与第三边，并且等于它的一半。 此性质的特点：同一条件下有2个结论 因为DE为ΔABC的中位线 所以①DE∥BC，②DE=½BC ↓ ↓ 位置关系 数量关系
如图1：在△ABC中，DE是中位线 （1）若∠ADE=60°， 则∠B= 度，为什么？ （2）若BC=8cm， 则DE= cm，为什么？
如图2：在△ABC中，D、E、F分别 是各边中点 AB=6cm，AC=8cm，BC=10cm， 则△DEF的周长= cm
求证：三角形的一条中位线与第三边上的中线互相平分。
证明:∵ AD＝DB，BE＝EC，∴ DE∥AC（三角形的中位线平行于第三边并且等于第三边的一半）．同理EF∥AB．∴四边形ADEF是平行四边形．∴ AE、DF互相平分（平行四边形的对角线互相平分）．
已知：　如图24．4．3所示，在△ABC中，AD＝DB，BE＝EC，AF＝FC．求证：　AE、DF互相平分．
例2、如图24．4．4，△ABC中，D、E分别是边BC、AB的中点，AD、CE相交于G．求证：　
∵　D、E分别是边BC、AB的中点，
（三角形的中位线平行于第三边并且等于第三边的一半），
∴　△ACG∽△DEG，
2、若△ABC的三条中位线围成的三角形周长为15cm， △ABC的周长是____。
1、若△ABC三边AB、AC、BC的长分别为8、6、　　　　　　4，它的三条中位线围成的△DEF的周长_____。
3、若△ABC的三条中位线长分别为3、4、5，则△ABC的周长为 面积为 。
　4、已知：　在四边形ABCD中，AD＝BC，P是对角线BD的中点，M是DC的中点，N是AB的中点．求证∠PMN＝∠PNM．
5、顺次连接四边形的四边中点所得的四边形是（ 　） （A）四边形 （B）平行四边形 （C）矩形 （D）菱形
１．理解三角形中位线的概念：连接三角形两边的中点的线段叫做三角形的中位线。２．掌握三角形中位线的性质：三角形的中位线平行与第三边，并且等于它的一半。3．能应用三角形中位线的性质解决有关计算或说理等问题。
1. （2014•白银）D、E分别是不等边三角形ABC（即AB≠BC≠AC）的边AB、AC的中点．O是△ABC所在平面上的动点，连接OB、OC，点G、F分别是OB、OC的中点，顺次连接点D、G、F、E．（1）如图，当点O在△ABC的内部时，求证：四边形DGFE是平行四边形；（2）若四边形DGFE是菱形，则OA与BC应满足怎样的数量关系？（直接写出答案，不需要说明理由．）
2. （2014•南京）如图，在△ABC中，D、E分别是AB、AC的中点，过点E作EF∥AB，交BC于点F．（1）求证：四边形DBFE是平行四边形；（2）当△ABC满足什么条件时，四边形DBFE是菱形？为什么？