











高中数学人教A版 (2019)必修 第二册8.5 空间直线、平面的平行备课ppt课件
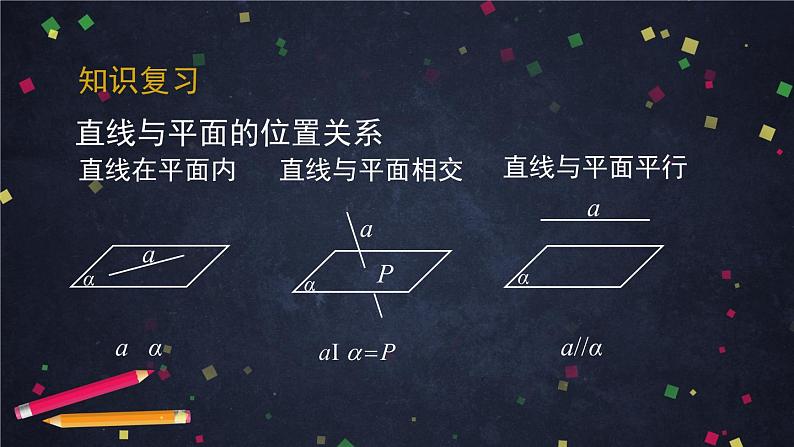
展开请大家回顾直线与平面的位置关系有几种?分别是什么?
在直线与平面的位置关系中,平行是一种非常重要的关系.它不仅应用广泛,而且是学习平面与平面平行的基础.本节课主要研究直线与平面平行的判定与性质.
在日常生活中,哪些实例给我们以直线与平面平行的印象呢?
我们知道根据定义,判定直线与平面是否平行,只需判定直线与平面有没有公共点.但是,直线是无限延伸的,平面是无限延展的,如何保证直线与平面没有公共点呢?
(1)观察如图8.5-6(1),门扇的两边是平行的.当门扇绕着一边转动时,另一边与墙面有公共点吗?此时门扇转动的一边与墙面平行吗?
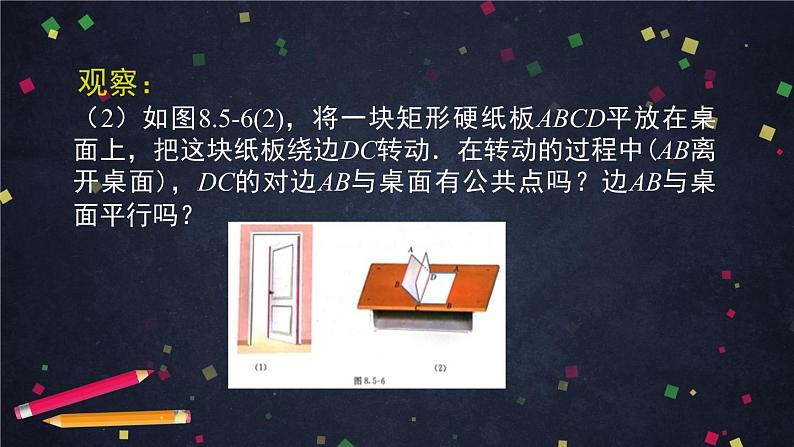
(2)如图8.5-6(2),将一块矩形硬纸板ABCD平放在桌面上,把这块纸板绕边DC转动.在转动的过程中(AB离开桌面),DC的对边AB与桌面有公共点吗?边AB与桌面平行吗?
(3)根据以上实例,你能总结一条直线与一个平面平行的充分条件吗?
共性:线(面外) //线(面内) 线(面外) //面
定理 若平面外一条直线与此平面内的一条直线 平行,则该直线与此平面平行.
请同学们考虑用图形语言和符号语言如何表示定理?
你能对直线与平面平行的判定定理作出合理的解释吗?
分析:因为直线a与b平行,所以它们没有公共点.在平面α内平移b ,得到直线c,不难发现a//c.无数条与a平行的直线无限细密地“铺满”平面α.则平面α内的任一点均在直线a的某条平行线上,于是,直线a与平面α没有公共点,即a// α.
定理告诉我们,可以通过直线间的平行,得到直线与平面平行.这是处理空间位置关系的一种常用方法,即将直线与平面的平行关系(空间问题)转化为直线间的平行关系(平面问题).
这一定理在现实生活中有许多应用.例如,安装矩形镜子时,为了使镜子的上边框与天花板平行,只需镜子的上边框与天花板和墙面的交线平行,就是应用了这个判定定理.你还能举出其他一些应用实例吗?
例题 判断下列命题是否正确,正确的打“√”,错误的打“×”.
(1)若一条直线不在平面内,则该直线与此平面平行( )
总结 这提醒我们,可以通过直线间的平行,得到直线与平面平行.但是,在运用直线与平面平行的判定定理解决问题时,一定要注意定理的条件:即平面外的一条直线与平面内的一条直线平行,才能够得出相应的线面平行关系.
例题 求证:空间四边形相邻两边中点的连线平行于经过另外两边的平面.
已知:如图,空间四边形ABCD中,E,F分别是 AB,AD的中点.求证: EF//平面BCD.
例题 已知:如图,空间四边形ABCD中,E,F分别是 AB,AD的中点.求证: EF//平面BCD.
证明:连接BD.∵ AE=EB,AF=FD,∴ EF//BD.又 EF 平面BCD,BD 平面BCD,∴ EF//平面BCD.
前面,我们利用平面内的直线与平面外的直线平行,得到了判定平面外的直线与此平面平行的方法,即得到了一条直线与平面平行的充分条件.反过来,如果一条直线与一个平面平行,能推出哪些结论呢?
下面我们研究在直线a平行于平面α的条件下, 直线a与平面α内的直线有怎样的位置关系呢? 在什么条件下,平面α内的直线与直线a平行呢?
分析:假设a与α内的直线b平行,那么由基本事实的推论3,过直线a,b有唯一的平面β.这样,我们可以把直线b看成是过直线a的平面β与平面α的交线.于是可以得如下结论:过直线a的平面β与平面α相交于b,则a//b.
如图,已知a//α, a β, α∩β=b.求证:a//b.证明:∵ α∩β=b, ∴ b α.又 a//α, ∴ a与b无公共点.又 a β, b β, ∴ a//b.
定理 一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行.
直线与平面平行的性质定理揭示了直线与平面平行中蕴含着直线与直线平行,这也给出了一种作平行线的方法.
例题 如图所示的一块木料中,棱BC平行于面A′C′.
(1)要经过面A′C′内的一点P和棱BC将木料锯开,在木料表面应该怎样画线?(2)所画的线与平面AC是什么位置关系?
分析:要经过面A′C′内的一点P和棱BC将木料锯开,实际上是经过BC及BC外一点P作截面,也就需要找出所作的截面与相关平面的交线.我们可以依据直线与平面平行的性质定理、基本事实4和推论1画出所需要的线段.
(1)要经过面A′C′内的一点P和棱BC将木料锯开,在木料表面应该怎样画线?
解:(1)如图,在平面A′C′内,过点P 作直线EF,使EF//B′C′,并分别交棱A′B′,D′C′于点E,F. 连接BE,CF,则EF,BE,CF就是应画的线.
(2)所画的线与平面AC是什么位置关系?
解:(2)因为棱BC平行于平面A′C′,平面BC′与平面A′C′相交于B′C′,所以BC//B′C′.由(1)知, EF//B′C′,所以EF//BC.而BC在平面AC内,EF在平面AC外,所以EF//平面AC.显然, BE,CF都与平面AC相交.
例题 如图,已知P是平行四边形ABCD所在平面外一点,M,N分别是AB、PC的中点,平面PAD∩平面PBC=l.
(1)求证:l//BC;(2)MN与平面APD是否平行? 试证明你的结论.
(1)求证:l//BC;
证明: ∵ BC//AD, BC 平面PAD,AD 平面PAD,∴ BC//平面PAD.又∵ 平面PBC∩平面PAD=l,∴ BC//l.
(2)MN与平面APD是否平行? 试证明你的结论.
例题(2)MN与平面APD是否平行?试证明你的结论.
解:平行.证明如下:取PD的中点E,连接AE,NE.可证NE//AM且NE=AM.∴ 四边形AMNE为平行四边形.∴ MN//AE.又 MN 平面PAD,AE 平面PAD,∴ MN//平面PAD.
1.如图,在长方体ABCD-A′B′C′D′中,(1)与AB平行的平面是 ; (2)与AA′平行的平面是 ; (3)与AD平行的平面是 .
解析:(1)平面A′B′C′D′,平面DCC′D′;(2)平面DCC′D′,平面BB′C′C;(3)平面A′B′C′D′,平面BCC′B′.
2.如图,在正方体ABCD-A1B1C1D1中,E为DD1的中点,判断BD1与平面AEC的位置关系,并说明理由.
解:BD1//平面AEC.证明如下:连接BD,与AC交于点O,连接EO.∵ E,O分别是DD1 ,DB的中点 ,∴ BD1//EO.又∵ BD1 平面AEC, EO 平面AEC.∴ BD1//平面AEC.
(1)如果直线a//b,那么a平行于经过b的任何平面. (2)如果直线a和平面α满足a//α,那么a与α内的任 何直线平行. (3)如果直线a,b和平面α满足a//α, b//α,那a//b. (4)如果直线a,b和平面α满足a//b,a//α, , 那么,b//α.
3.判断下列命题,正确的打“√”,错误的打“×”.
(1)如果直线a//b,那么a平行于经过b的任何平面.
(2)如果直线a和平面α满足a//α,那么a与α内的任 何直线平行.
(3)如果直线a,b和平面α满足a//α,b//α,那a//b.
(4)如果直线a,b和平面α满足a//b,a//α, , 那么, b//α.
(1)如果直线a//b,那么a平行于经过b的任何平面. (2)如果直线a和平面α满足a//α,那么a与α内的任 何直线平行. (3)如果直线a,b和平面α满足a//α, b//α,那a//b. (4)如果直线a,b和平面α满足a//b,a//α, , 那么,b//α.
解析:(1)×;(2)×;(3)×;(4)√.
4.如图,α∩β=a,b α,c β,b//c,求证:a//b//c.
证明:∵ b//c,c β,b β,∴ b//β.又 b α, α∩β=a ,∴ b//a.∴ a//b//c .
小结:我们本节课学习了空间中直线与平面平行的判定定理和性质定理,大家思考:
1.你能用三种数学语言表达直线与平面平行的判定定理和性质定理吗?2.你又学会了哪些证明线线平行,线面平行的方法?3.运用定理解决问题的关键是什么?4.处理立体几何问题时常用的基本思想方法是什么?
空间直线、平面间的平行关系:
平行线的定义以及平面几何中判定两直线平行的定理
直线与平面平行的判定定理
直线与平面平行的性质定理
1.如图在四面体D-ABC中, E, F,G分别是AB,BC, CD的中点,求证: (1)AC//平面EFG. (2) BD//平面EFG.
高中8.4 空间点、直线、平面之间的位置关系备课ppt课件: 这是一份高中8.4 空间点、直线、平面之间的位置关系备课ppt课件,文件包含高一数学人教A版841平面课件pptx、841平面同步练习含解析doc、高一数学人教A版841平面教案docx等3份课件配套教学资源,其中PPT共60页, 欢迎下载使用。
2021学年8.6 空间直线、平面的垂直图文ppt课件: 这是一份2021学年8.6 空间直线、平面的垂直图文ppt课件,文件包含高一数学人教A版861直线与直线垂直课件pptx、861直线与直线垂直同步练习含解析doc、高一数学人教A版861直线与直线垂直教案docx等3份课件配套教学资源,其中PPT共52页, 欢迎下载使用。
高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直课堂教学课件ppt: 这是一份高中数学人教A版 (2019)必修 第二册8.6 空间直线、平面的垂直课堂教学课件ppt,文件包含高一数学人教A版8621直线与平面垂直的概念及判定课件pptx、高一数学人教A版8621直线与平面垂直的概念及判定教案docx等2份课件配套教学资源,其中PPT共60页, 欢迎下载使用。













