初中数学沪科版八年级上册15.2 线段的垂直平分线优秀课件ppt

这是一份初中数学沪科版八年级上册15.2 线段的垂直平分线优秀课件ppt，共34页。PPT课件主要包含了新课导入，讲授新课，当堂练习，课堂小结等内容，欢迎下载使用。

市政府为了方便居民的生活，计划在三个住宅小区A、B、C之间修建一个购物中心，试问，该购物中心应建于何处才能使得它到三个小区的距离相等?
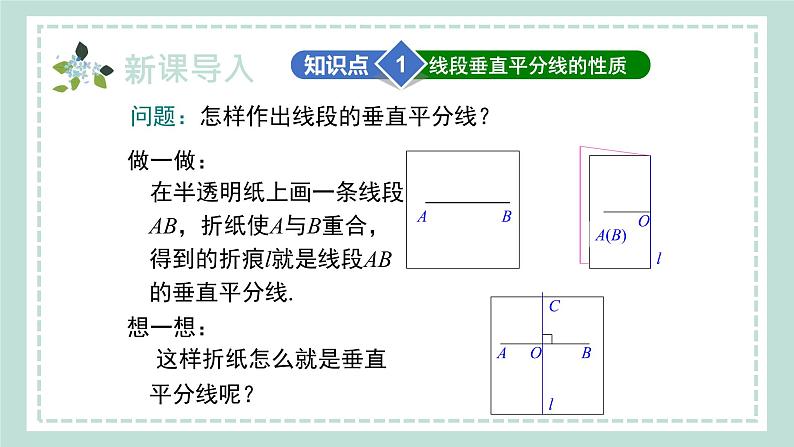
问题：怎样作出线段的垂直平分线？
做一做： 在半透明纸上画一条线段AB，折纸使A与B重合，得到的折痕l就是线段AB的垂直平分线.想一想： 这样折纸怎么就是垂直平分线呢？
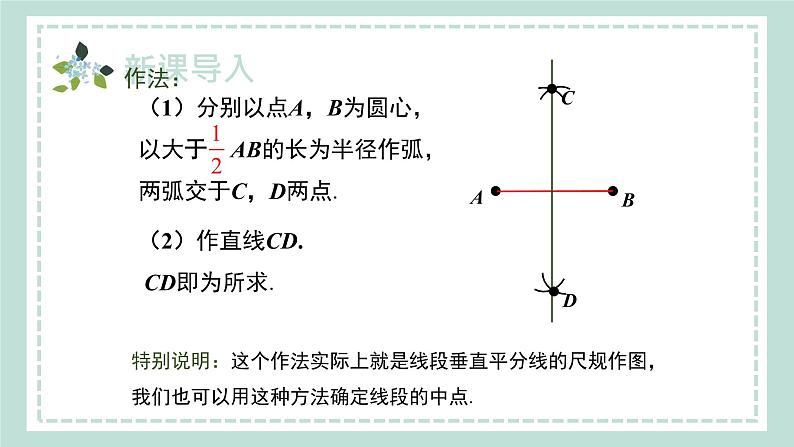
（2）作直线CD. CD即为所求.
特别说明：这个作法实际上就是线段垂直平分线的尺规作图，我们也可以用这种方法确定线段的中点.
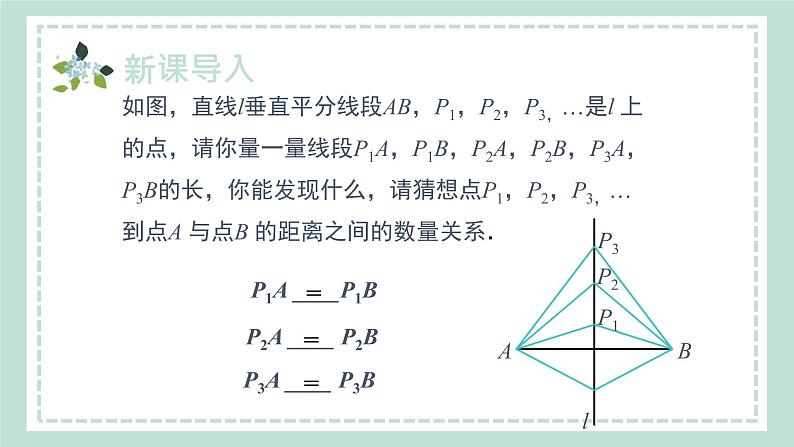
如图，直线l垂直平分线段AB，P1，P2，P3，…是l 上的点，请你量一量线段P1A，P1B，P2A，P2B，P3A，P3B的长，你能发现什么，请猜想点P1，P2，P3，… 到点A 与点B 的距离之间的数量关系．
P1A ____P1B
P2A ____ P2B
P3A ____ P3B
猜想：点P1，P2，P3，… 到点A 与点B 的距离分别相等．
命题：线段垂直平分线上的点和这条线段两个端点的距离相等.
由此你能得到什么结论？
已知：如图，直线l⊥AB，垂足为C，AC =CB，点P 在l 上．求证：PA =PB．
　证明：∵　l⊥AB， ∴ ∠PCA =∠PCB．　　又 AC =CB，PC =PC，　　∴ △PCA ≌△PCB（SAS）．　　∴ PA =PB．
(山东临沂)如图，在四边形ABCD中，AC垂直平分BD， 垂足为E，下列结论不一定成立的是(　　) A．AB＝AD　　　　B．CA平分∠BCD C．AB＝BD D．△BEC≌△DEC 导引：根据线段垂直平分线的性质得出AB与AD的关系，结合三 角形全等对四个选项进行逐一验证． ∵AC垂直平分BD， ∴AB＝AD，BC＝DC， 又∵AC＝AC， ∴△ABC≌△ADC，∴∠BCA＝∠DCA. 又∵BC＝DC，CE＝CE， ∴△BEC≌△DEC，∴选项A，B，D成立．
如图，在△ABC中，AC＝5，AB的垂直 平分线DE交AB，AC于点E，D， (1)若△BCD的周长为8，求BC的长； (2) 若BC＝4，求△BCD的周长．导引：由DE是AB的垂直平分线，得AD＝BD，所以 BD与CD的长度和等于AC的长，所以由△BCD 的周长可求BC的长，同样由BC的长也可求△BCD的周长． 解：∵DE是AB的垂直平分线， ∴AD＝BD，∴BD＋CD＝AD＋CD＝AC＝5. (1)∵△BCD的周长为8， ∴BC＝△BCD的周长－(BD＋CD)＝8－5＝3. (2)∵BC＝4， ∴△BCD的周长＝BC＋BD＋CD＝5＋4＝9.
练一练：1.如图①所示，直线CD是线段AB的垂直平分线，点P为直线CD上的一点，且PA=5，则线段PB的长为（ ）A. 6 B. 5 C. 4 D. 3
2.如图②所示，在△ABC中，BC=8cm,边AB的垂直平分线交AB于点D，交边AC于点E, △BCE的周长等于18cm,则AC的长是 .
如图，已知点A、点B以及直线l.(1)用尺规作图的方法在直线l上求作一点P，使PA＝PB.(保留作图痕迹，不要求写出作法)；(2)在(1)中所作的图中，若AM＝PN，BN＝PM，求证：∠MAP＝∠NPB.
(2)在△AMP和△BNP中，∵AM=PN，AP＝BP，PM＝BN， ∴△AMP≌△PNB(SSS)，∴∠MAP＝∠NPB.
如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F.求证：(1)FC＝AD；(2)AB＝BC＋AD.
解析：(1)根据AD∥BC可知∠ADC＝∠ECF，再根据E是CD的中点可求出△ADE≌△FCE，根据全等三角形的性质即可解答．(2)根据线段垂直平分线的性质判断出AB＝BF即可．
证明：(1)∵AD∥BC，∴∠ADC＝∠ECF.∵E是CD的中点，∴DE＝EC.又∵∠AED＝∠CEF，∴△ADE≌△FCE，∴FC＝AD.(2)∵△ADE≌△FCE，∴AE＝EF，AD＝CF.∵BE⊥AE，∴BE是线段AF的垂直平分线，∴AB＝BF＝BC＋CF.∵AD＝CF，∴AB＝BC＋AD.
定理：线段垂直平分线上的点到线段两端的距离相等.
到线段两端距离相等的点在线段的垂直平分线上.
它是真命题吗？你能证明吗？
已知：PA=PB，求证：点P在线段AB的垂直平分线上.
证明：作PC⊥AB,垂足为C.
∴∠ACP=∠BCP=90°.
在Rt△ACP和Rt△BCP中，
∴Rt△ACP≌Rt△BCP（HL），
∴点P在线段AB的垂直平分线上.
PA=PB，PC=PC，
到线段两端距离相等的点在线段的垂直平分线上．
应用格式：∵　PA =PB，∴　点P 在AB 的垂直平分线上．
作用：判断一个点是否在线段的垂直平分线上.
如图,已知△ABC的边AB,AC的垂直平分线相交于点P. 求证:点P在BC的垂直平分线上.
证明：连接PA，PB，PC. ∵点P在AB，AC的垂直平分线上， ∴PA=PB，PA=PC， （线段垂直平分线上的点到线段两端距离相等） ∴PB=PC，（等式性质） ∴点P在BC的垂直平分线上. (与线段两端距离相等的点在这条线段的垂直平分线上）
三角形三边的垂直平分线相交于一点，这点到三角形三个顶点的距离相等.
现在你能回答讲课前提出的问题吗？你知道购物中心应该建在何处了吗？
已知：如图，点E是∠AOB的平分线上一点，EC⊥OA,ED⊥OB,垂足分别为C,D，连接CD.求证：OE是CD的垂直平分线.
∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴ OE是CD的垂直平分线.
又∵OE=OE，∴Rt△OED≌Rt△OEC.
2.在锐角三角形ABC内一点P,，满足PA=PB=PC,则点P是△ABC ( )A.三条角平分线的交点B.三条中线的交点C.三条高的交点D.三边垂直平分线的交点
4.下列说法：①若点P、E是线段AB的垂直平分线上两点，则EA＝EB，PA＝PB；②若PA＝PB，EA＝EB，则直线PE垂直平分线段AB；③若PA＝PB，则点P必是线段AB的垂直平分线上的点；④若EA＝EB，则经过点E的直线垂直平分线段AB．其中正确的有 （填序号）.
3.已知线段AB，在平面上找到三个点D、E、F，使DA＝DB，EA＝EB,FA＝FB，这样的点的组合共有　　　　种.
5.如图，△ABC中，AB=AC,AB的垂直平分线交AC于E,连接BE，AB+BC=16cm,则△BCE的周长是 cm.
6.已知：如图，点C，D是线段AB外的两点，且AC =BC， AD=BD，AB与CD相交于点O. 求证：AO=BO.
证明： ∵ AC =BC，AD=BD，
∴ CD为线段AB的垂直平分线.
又 ∵AB与CD相交于点O，
7.如图，有A，B，C三个村庄，现准备要建一所希望小学，要求学校到三个村庄的距离相等，请你确定学校的位置.
学校在连接任意两点的两条线段的垂直平分线的交点处.
8.如图所示，在△ABC中，AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，试说明AD与EF的关系．
解：AD垂直平分EF.∵AD平分∠BAC，DE⊥AB，DF⊥AC，∴∠EAD＝∠FAD，∠AED＝∠AFD=90°.又∵AD＝AD，∴△ADE≌△ADF，∴AE＝AF，DE＝DF.∴A、D均在线段EF的垂直平分线上，即直线AD垂直平分线段EF.
线段的垂直平分的性质和判定
到线段的两个端点距离相等的点在线段的垂直平分线上
线段的垂直平分线上的点到线段的两个端点的距离相等
见垂直平分线，得线段相等
判断一个点是否在线段的垂直平分线上