数学九年级上册25.4 相似三角形的判定课时练习

这是一份数学九年级上册25.4 相似三角形的判定课时练习，共16页。试卷主要包含了如图，△OAB∽△OCD，OA等内容，欢迎下载使用。

2021-2022学年冀教版九年级数学上册《25.5相似三角形的性质》同步达标测评（附答案）
一．选择题（共10小题，满分50分）
1．若△ABC∽△DEF，若∠A＝50°，则∠D的度数是（　　）
A．50° B．60° C．70° D．80°
2．若△ABC∽△DEF且面积比为9：25，则△ABC与△DEF的周长之比为（　　）
A．9：25 B．3：25 C．3：5 D．2：5
3．已知△ABC∽△A'B'C'，AD和A'D'是它们的对应中线，若AD＝10，A'D'＝6，则△ABC与△A'B'C'的周长比是（　　）
A．3：5 B．9：25 C．5：3 D．25：9
4．已知△ABC∽△DEF，且△ABC与△DEF的面积比为9：4，△ABC的最短边为4.5cm，则△DEF的最短边为（　　）
A．6cm B．2cm C．3cm D．4cm
5．已知△ABC∼△DEF，且△ABC的面积为2cm2，△DEF的面积为8cm2，则△ABC与△DEF的相似比是（　　）
A．1：4 B．4：1 C．1：2 D．2：1
6．如图，△ABC∽△ADE，且BC＝2DE，则的值为（　　）

A． B． C． D．
7．如图，△OAB∽△OCD，OA：OC＝3：2，∠A＝α，∠C＝β，△OAB与△OCD的面积分别是S1和S2，△OAB与△OCD的周长分别是C1和C2，则下列等式一定成立的是（　　）

A． B． C． D．
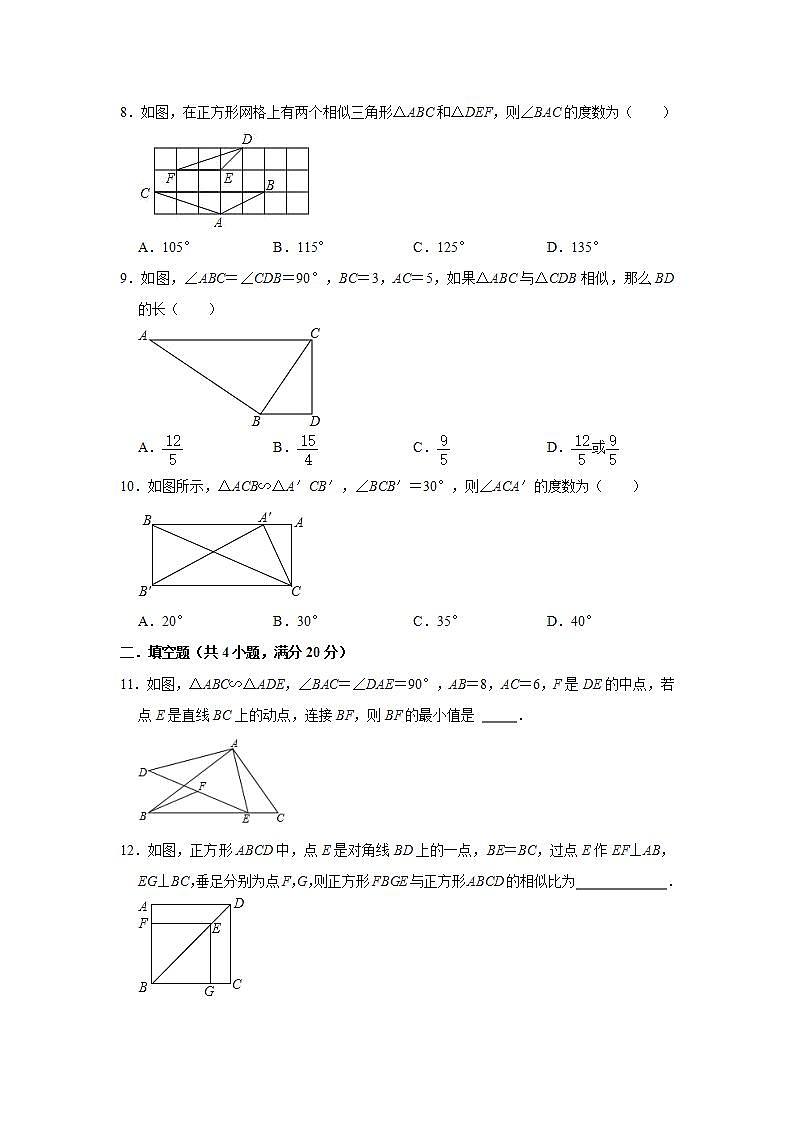
8．如图，在正方形网格上有两个相似三角形△ABC和△DEF，则∠BAC的度数为（　　）

A．105° B．115° C．125° D．135°
9．如图，∠ABC＝∠CDB＝90°，BC＝3，AC＝5，如果△ABC与△CDB相似，那么BD的长（　　）

A． B． C． D．或
10．如图所示，△ACB∽△A′CB′，∠BCB′＝30°，则∠ACA′的度数为（　　）

A．20° B．30° C．35° D．40°
二．填空题（共4小题，满分20分）
11．如图，△ABC∽△ADE，∠BAC＝∠DAE＝90°，AB＝8，AC＝6，F是DE的中点，若点E是直线BC上的动点，连接BF，则BF的最小值是 　 　．

12．如图，正方形ABCD中，点E是对角线BD上的一点，BE＝BC，过点E作EF⊥AB，EG⊥BC，垂足分别为点F，G，则正方形FBGE与正方形ABCD的相似比为　 　．


13．如图，Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，D是AB边的中点，P是BC边上一动点（点P不与B、C重合），若以D、C、P为顶点的三角形与△ABC相似，则线段PC＝　 　．

14．如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝4．翻折∠C，使点C落在斜边上某一点D处，折痕为EF（点E、F分别在边AC、BC上）．若△CEF与△ABC相似，则AD的长为　 　．

三．解答题（共6小题，满分50分）
15．先阅读下列材料，然后解答问题．
材料：从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线例如：如图①，AD把△ABC分成△ABD与△ADC，若△ABD是等腰三角形，且△ADC∽△BAC，那么AD就是△ABC的完美分割线．
解答下列问题：
（1）如图②，在△ABC中，∠B＝40°，AD是△ABC的完美分割线，且△ABD是以AD为底边的等腰三角形，
则∠CAD＝　 　度．
（2）在△ABC中，∠B＝42°，AD是△ABC的完美分割线，且△ABD是等腰三角形，求∠BAC的度数．

16．如图，在四边形ABCD中，AB∥DC，CB⊥AB．AB＝16cm，BC＝6cm，CD＝8cm，动点P从点D开始沿DA边匀速运动，动点Q从点A开始沿AB边匀速运动，它们的运动速度均为2cm/s．点P和点Q同时出发，设运动的时间为t（s），0＜t＜5．
（1）用含t的代数式表示AP；
（2）当以点A．P，Q为顶点的三角形与△ABD相似时，求t的值；
（3）当QP⊥BD时，求t的值．


17．求证：相似三角形对应角的角平分线之比等于相似比．
要求：①分别在给出的△ABC与△DEF中用尺规作出一组对应角的平分线，不写作法，保留作图痕迹；
②在完成作图的基础上，写出已知、求证，并加以证明．


18．求证：相似三角形面积的比等于相似比的平方．（请根据题意画出图形，写出已知，求证并证明）

19．（1）如图1，Rt△ABC中，若AC＝4，BC＝3，DE⊥AC，且DE＝DB，求AD的长；
（2）如图2，已知△ABC，若AB边上存在一点M，若AC边上存在一点N，使MB＝MN，且△AMN∽△ABC，请利用没有刻度的直尺和圆规，作出符合条件的线段MN（注：不写作法，保留作图痕迹，对图中涉及到的点用字母进行标注）．

20．定义：在△ABC中，点D，E，F分别是边AB，BC，CA上的动点，若△DEF∽△ABC（点D、E、F的对应点分别为点A、B、C），则称△DEF是△ABC的子三角形，如图．
（1）已知：如图1，△ABC是等边三角形，点D，E，F分别是边AB，BC，CA上动点，且AD＝BE＝CF．
求证：△DEF是△ABC的子三角形．
（2）已知：如图2，△DEF是△ABC的子三角形，且AB＝AC，∠A＝90°，若BE＝，求CF和AD的长．


参考答案
一．选择题（共10小题）
1．解：∵△ABC∽△DEF，∠A＝50°，
∴∠D＝∠A＝50°．
故选：A．
2．解：∵相似三角形△ABC与△DEF面积的比为9：25，
∴它们的相似比为3：5，
∴△ABC与△DEF的周长比为3：5．
故选：C．
3．解：∵△ABC∽△A'B'C'，AD和A'D'是它们的对应中线，AD＝10，A'D'＝6，
∴△ABC与△A'B'C'的周长比＝AD：A′D′＝10：6＝5：3．
故选：C．
4．解：设△DEF的最短边边长是xcm，
∵△ABC∽△DEF，面积比为9：4，
∴△ABC与△DEF的对应边之比3：2．
∴4.5：x＝3：2．
则x＝3．
故选：C．
5．解：∵△ABC的面积为2cm2，△DEF的面积为8cm2，
∴△ABC与△DEF的面积比为1：4，
∵△ABC∼△DEF，
∴△ABC与△DEF的相似比为1：2，
故选：C．
6．解：∵△ABC∽△ADE，且BC＝2DE，
∴，
∴，
故选：B．
7．解：∵△OAB∽△OCD，OA：OC＝3：2，∠A＝α，∠C＝β，
∴，A错误；
∴，C错误；
∴，D正确；
不能得出，B错误；
故选：D．
8．解：∵EF＝2，DE＝，DF＝，BC＝5，AB＝，AB＝，
∴＝＝＝，
∴△ABC∽△EDF，
∴∠BAC＝∠DEF，
又∵∠DEF＝90°+45°＝135°，
∴∠BAC＝135°，
故选：D．
9．解：分两种情况：
①∵△ABC∽△CDB，
∴AC：BC＝BC：BD，
即5：3＝3：BD，
∴5BD＝9，
∴BD＝；
②由勾股定理得：AB＝＝4，
∵△ABC∽△BDC，
∴，
即，
解得：BD＝；
综上可知：BD的长为或；
故选：D．
10．解：∵△ACB∽△A′CB′，
∴∠ACB＝∠A′CB′，
∴∠ACB﹣∠A′CB＝∠A′CB′﹣∠A′CB，
∴∠ACA′＝∠BCB′，
∵∠BCB′＝30°，
∴∠ACA′＝30°，
故选：B．
二．填空题（共4小题，满分20分）
11．解：∵△ABC∽△ADE，
∴∠ADE＝∠ABE，
∴点A，D，B，E四点共圆，
∵∠DAE＝90°，
∴∠DBE＝90°，
∵F是DE的中点，
∴BF＝DE，
∴当DE最小时，BF的值最小，
∵若点E是直线BC上的动点，
∴当AE⊥BC时，AE最小，此时，DE最小，
∵∠BAC＝90°，AB＝8，AC＝6，
∴BC＝10，
∴AE＝＝＝，
∵△ABC∽△ADE，
∴＝，
∴＝，
∴DE＝8，
∴BF＝4，
故答案为：4．

12．解：设BG＝x，
则BE＝x，
∵BE＝BC，
∴BC＝x，
则正方形FBGE与正方形ABCD的相似比＝BG：BC＝x：x＝：2，
故答案为：．
13．解：∵Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，
∴AB＝10，
∵D是AB边的中点，
∴CD＝BD＝AB＝5，
∵以D、C、P为顶点的三角形与△ABC相似，
∴∠DPC＝90°或∠CDP＝90°，
（1）若∠DPC＝90°，则DP∥AC，
∴＝，
∴BP＝BC＝4，
则PC＝4；
（2）若∠CDP＝90°，则△CDP∽△BCA，
∴，
即，
∴PC＝．
∴PC＝4或．

14．解：若△CEF与△ABC相似，分两种情况：
①若CE：CF＝3：4，
∵CE：CF＝AC：BC，
∴EF∥AB．
由折叠性质可知，CD⊥EF，
∴CD⊥AB，即此时CD为AB边上的高．
在Rt△ABC中，∵∠ACB＝90°，AC＝3，BC＝4，
∴AB＝＝5，
∴AD＝；
②若CF：CE＝3：4，
∵△CEF∽△CBA，
∴∠CEF＝∠B．
由折叠性质可知，∠CEF+∠ECD＝90°，
又∵∠A+∠B＝90°，
∴∠A＝∠ECD，
∴AD＝CD．
同理可得：∠B＝∠FCD，CD＝BD，
∴D点为AB的中点，
∴AD＝AB＝
故答案为：或．
三．解答题（共6小题，满分50分）
15．解：（1）∵AD是△ABC的完美分割线，
∴△DAC∽△ABC
∴∠CAD＝∠B＝40°
故答案为：40
（2）若BD＝AD，
∵AD是△ABC的完美分割线，
∴△DAC∽△ABC
∴∠CAD＝∠B＝42°
∵AD＝BD，
∴∠ABD＝∠BAD＝42°
∴∠BAC＝∠BAD+∠CAD＝84°
若AB＝BD，
∴∠BAD＝69°＝∠BDA
∵AD是△ABC的完美分割线，
∴△DAC∽△ABC
∴∠CAD＝∠B＝42°
∴∠BAC＝∠BAD+∠CAD＝42°+69°＝111°
若AB＝AD，
∴∠B＝∠ADB＝42°
∵AD是△ABC的完美分割线，
∴△DAC∽△ABC
∴∠CAD＝∠B＝42°
∵∠ADB＝∠DAC+∠C＝42°+∠C≠42°
∴不存在AB＝AD，
综上所述：∠BAC的度数为84°或111°
16．解：（1）如图作DH⊥AB于H，则四边形DHBC是矩形，
∴CD＝BH＝8，DH＝BC＝6，
∴AH＝AB﹣BH＝8，AD＝＝10，
由题意AP＝AD﹣DP＝10﹣2t．
（2）当以点A．P，Q为顶点的三角形与△ABD相似时，
∴或，
∴＝或，
解得：t＝或t＝，
∴当t＝或t＝时，当以点A，P，Q为顶点的三角形与△ABD相似；
（3）过P作PN⊥AB于N，
当PQ⊥BD时，∠PQN+∠DBA＝90°，
∵∠QPN+∠PQN＝90°，
∴∠QPN＝∠DBA，
∴＝，
解得t＝，
经检验：t＝是分式方程的解，
∴当t＝s时，PQ⊥BD．

17．解：①如图所示，AG，DH分别是∠BAC与∠EDF的角平分线；
②已知：如图，△ABC∽△DEF，＝＝＝k，AG，DH分别是∠BAC与∠EDF的角平分线．
求证：＝k；
证明：∵AG，DH分别是△ABC与△DEF的角平分线，
∴∠BAG＝∠BAC，∠EDH＝∠EDF，
∵△ABC∽△DEF，
∴∠BAC＝∠EDF，∠B＝∠E，
∴∠BAG＝∠EDH，
∴△ABG∽△DEH，
∴＝＝k．

18．已知：如图，已知△ABC∽△A1B1C1，顶点A、B、C分别与A1、B1、C1对应，△ABC和△A1B1C1的相似比为k．
求证：＝k2；
证明：作AD⊥BC于D，A1D1⊥B1C1于D1，
∵△ABC∽△A1B1C1，顶点A、B、C分别与A1、B1、C1对应，
∴∠B＝∠B1，
∵AD、A1D1分别是△ABC，△A1B1C1的高线，
∴∠BDA＝∠B1D1A1，
∴△ABD∽△A1B1D1，
∴＝＝k，
∴＝＝k2．

19．解：（1）在Rt△ABC中，AC＝4，BC＝3，
∴AB＝5，
∵DE⊥AC，∠C＝90°，
∴DE∥BC，
∴△ADE∽△ABC，
∴，
即，
解得AD＝，
故AD的长为．
（2）
如图2所示，作∠B的平分线BN，交AC于N，作BN的垂直平分线MG，交AB于M，MN即为所求．
20．（1）证明：如图1中，

∵△ABC是等边三角形，
∴AB＝BC＝AC，∠A＝∠B＝∠C＝60°，
∵AD＝BE＝CF，
∴AF＝BD＝CE，
∴△DAF≌△EBD≌△FCE，
∴DE＝EF＝DF，
∴△DEF是等边三角形，
∴∠DEF＝∠EDF＝∠B＝∠A＝60°，
∴△DEF∽△ABC．
∴△DEF是△ABC的子三角形．
（2）如图2中，作EH⊥AB于H．

∵AB＝AC，∠BAC＝90°，
∴∠B＝∠C＝45°，
∵△DEF是△ABC的子三角形，
∴△DEF∽△ABC，
∴DE＝DF，∠EDF＝90°，
∴∠ADF+∠AFD＝90°，∠ADF+∠EDH＝90°，
∴∠EDH＝∠AFD，
∵∠DHE＝∠A＝90°，
∴△DEH≌△DFA，
∴AD＝HE，
∵△BEH是等腰直角三角形，
∴HE＝×＝1，
∴AD＝1，
∵∠DEC＝∠DEF+∠FEC＝∠B+∠BDE，
∵∠B＝∠DEF＝45°，
∴△BDE∽△CEF，
∴＝＝，
∴CF＝2．