数学九年级上册第25章 图形的相似25.4 相似三角形的判定第3课时教学设计及反思

25．4  相似三角形的判定第3课时 

第3课时  相似三角形的判定定理3

1．理解“三边对应成比例的两个三角形相似”的判定方法；(重点)

2．会运用“三边对应成比例的两个三角形相似”的判定方法解决简单问题．（重点、难点）

一、情境导入

我们现在判定两个三角形是否相似，必须要知道它们的对应角是否相等，对应边是否成比例．那么是否存在判定两个三角形相似的简便方法呢？

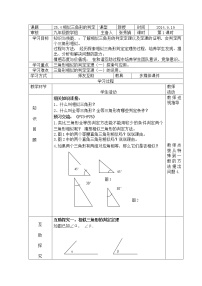
在如图所示的方格上任画一个三角形，再画第二个三角形，使它的三边长都是原来三角形的三边长的相同倍数．画完之后，用量角器比较两个三角形的对应角，你发现了什么结论？大家的结论都一样吗？

二、合作探究

探究点一：相似三角形的判定定理3

【类型一】 直接利用三边对应成比例的两个三角形相似判定两个三角形相似

  已知△ABC的三边长分别为1，，，△DEF的三边长分别为，，2，试判断△ABC与△DEF是否相似．

解析：因为已知两个三角形的三边长，所以可以考虑根据三边之间的比例关系来判定两个三角形是否相似．

解：∵＝＝，∴△ABC与△DEF相似．

方法总结：已知两个三角形三边的大小，要判断它们是否相似，关键是通过计算来说明三边是否对应成比例．在相似三角形中，最短（长）边与最短（长）边是对应边，所以在判定两个三角形的三边是否成比例时，应先确定边的大小，以便找准对应关系．

变式训练：见《学练优》本课时练习第1题

【类型二】  两组对应边的比相等的两个直角三角形相似

  在Rt△ABC中，∠C＝90°，AB＝10，BC＝6，在Rt△EDF中，∠F＝90°，DF＝3，EF＝4，则△ABC和△EDF相似吗？为什么？

解析：已知△ABC和△EDF都是直角三角形，且已知两条边长，所以可利用勾股定理分别求出第三边的长，看对应边是否对应成比例．

解：△ABC∽△EDF．理由如下：在Rt△ABC中，AB＝10，BC＝6，∠C＝90°，由勾股定理得AC＝＝＝8．在Rt△DEF中，DF＝3，EF＝4，∠F＝90°，由勾股定理得ED＝＝＝5．在△ABC和△EDF中，＝＝2，＝＝2，＝＝2，∴＝＝.∴△ABC∽△EDF．

方法总结：利用三边对应成比例判定两个三角形相似时，应说明三角形的三边对应成比例，而不是两边对应成比例．

变式训练：见《学练优》本课时练习第8题

【类型三】 网格中的相似三角形

  如图，在边长为1的小正方形组成的网格中，△ABC和△DEF的顶点都在格点上，判断△ABC和△DEF是否相似，并说明理由．

解析：首先由勾股定理，求得△ABC和△DEF的各边的长，即可得＝＝，然后由三组对应边的比相等的两个三角形相似，即可判定△ABC和△DEF相似．

解：△ABC和△DEF相似．理由如下：由勾股定理，得AB＝2，AC＝，BC＝5，DE＝4，DF＝2，EF＝2.∵＝＝＝＝＝，∴△ABC∽△DEF．

方法总结：在网格中计算线段的长，运用勾股定理是常用的方法．

变式训练：见《学练优》本课时练习第3题、第15题

探究点二：相似三角形判定定理3与性质的综合

【类型一】 利用相似三角形探究角的关系

  如图，已知＝＝，找出图中相等的角，并说明你的理由（仅考虑图中字母可以表示的角）．

解析：由＝＝，证明△ABC∽△ADE，再利用相似三角形对应角相等求解．

解：在△ABC和△ADE中，∵＝＝，∴△ABC∽△ADE.∴∠BAC＝∠DAE，∠B＝∠D，∠C＝∠E．

∴∠BAD＝∠CAE.

方法总结：在证明角相等时，可通过证明三角形相似得到．

变式训练：见《学练优》本课时练习第5题

【类型二】 利用相似三角形的判定解决探究性问题

  要制作两个形状相同的三角形教具，其中一个三角形教具的三边长分别为50 cm，60 cm，80 cm，另一个三角形教具的一边长为20 cm，请问怎样选料可使这两个三角形教具相似？想想看，有几种设计方案．

解析：要使两个三角形相似，已知一个三角形的三边和另一个三角形的一边，则我们可以采用三边分别对应成比例的两个三角形相似来判定．

解：①当长为20 cm的边长的对应边为50 cm时，∵50∶20＝5∶2，且第一个三角形教具的三边长分别是50 cm，60 cm，80 cm，∴另一个三角形对应的三边分别是20 cm，24 cm，32 cm；②当长为20 cm的边长的对应边为60 cm时，∵60∶20＝3∶1，且第一个三角形教具的三边长分别是50 cm，60 cm，80 cm，∴另一个三角形对应的三边分别是 cm，20 cm， cm；③当长为20 cm的边长的对应边为80 cm时，∵80∶20＝4∶1，且第一个三角形教具的三边长分别是50 cm，60 cm，80 cm，∴另一个三角形对应的三边分别是12．5 cm，15 cm，20 cm．∴有三种设计方案．

方法总结：解答此题的关键在于分类讨论，当对应比不确定时，采用分类讨论的方法可避免漏解．

变式训练：见《学练优》本课时练习第9题

三、板书设计

1．三角形相似的判定定理3：三边对应成比例的两个三角形相似；

2．相似三角形的判定定理3与性质的综合．

因为本课时教学过程中主要是让学生采用类比的方法先猜想出命题，然后证明猜想的命题是否正确．感受两个三角形相似的判定定理3与全等三角形判定定理（SSS）的区别与联系，体会事物间一般到特殊、特殊到一般的关系．让学生经历从实验探究到归纳证明的过程，发展学生的合情推理能力，培养学生与他人交流、合作的意识和品质．课堂上教师主要还是以提问的形式，逐步引导学生去证明命题．从课后作业情况看出学生对这节课的知识总体掌握得较好．

第2课时