高中数学人教A版 (2019)必修 第二册6.2 平面向量的运算同步达标检测题

6.2.2 向量的减法运算

（用时45分钟）

【选题明细表】

基础巩固

1．下列运算中正确的是(　　)

A.－＝   B.－＝

C.－＝  D.－＝0

【答案】C

【解析】根据向量减法的几何意义，知－＝，所以C正确，A错误；B显然错误；对于D，－应该等于0，而不是0.

2．下列说法错误的是(　　)

A．若＋＝，则－＝

B．若＋＝，则＋＝

C．若＋＝，则－＝

D．若＋＝，则＋＝

【答案】D

【解析】由向量的减法就是向量加法的逆运算可知，A，B，C都正确．由相反向量定量知，共＋＝，则＋＝－－＝－(＋)＝－，故D错误．

3．有下列不等式或等式：

①|a|－|b|＜|a＋b|＜|a|＋|b|；

②|a|－|b|＝|a＋b|＝|a|＋|b|；

③|a|－|b|＝|a＋b|＜|a|＋|b|；

④|a|－|b|＜|a＋b|＝|a|＋|b|.

其中，一定不成立的个数是(　　)

A．0  B．1  C．2  D．3

【答案】A

【解析】①当a与b不共线时成立；②当a＝b＝0，或b＝0，a≠0时成立；③当a与b共线，方向相反，且|a|≥|b|时成立；④当a与b共线，且方向相同时成立．

4.可以写成：①＋；②－；③－；④－，其中正确的是(　　)

A．①②  B．②③  C．③④  D．①④

【答案】D

【解析】　由向量的加法及减法定义可知①④符合．

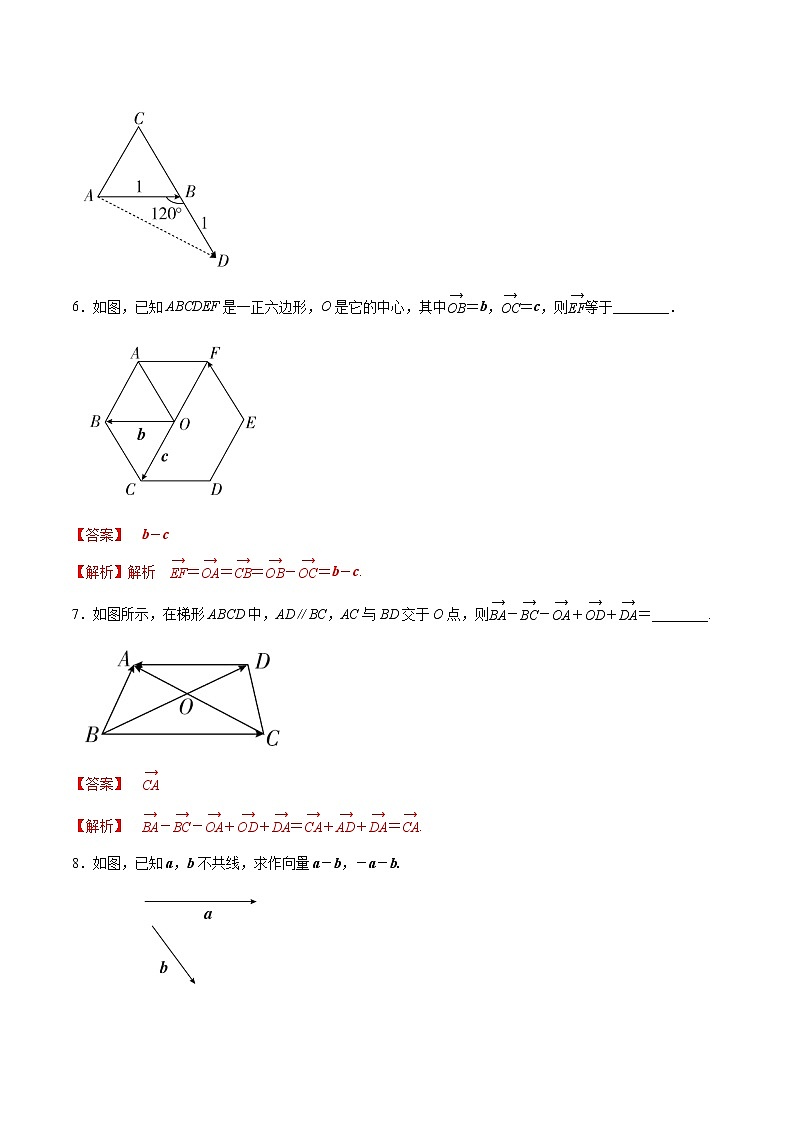
5．边长为1的正三角形ABC中，|－|的值为(　　)

A．1  B．2  C.  D.

【答案】D

【解析】　如图所示，延长CB到点D，使BD＝1，连接AD，则－＝＋＝＋＝.在△ABD中，AB＝BD＝1，∠ABD＝120°，易求AD＝，∴|－|＝.

6．如图，已知ABCDEF是一正六边形，O是它的中心，其中＝b，＝c，则等于________．

【答案】　b－c

【解析】解析　＝＝＝－＝b－c.

7．如图所示，在梯形ABCD中，AD∥BC，AC与BD交于O点，则－－＋＋＝________.

【答案】　

【解析】　－－＋＋＝＋＋＝.

8．如图，已知a，b不共线，求作向量a－b，－a－b.

【答案】　见解析

【解析】　如图(1)，在平面内任取一点O，作＝a，＝b，则＝－＝a－b.

如图(2)，在平面内任取一点O，作＝－a，＝b，则＝－＝－a－b.

能力提升

9．平面上有三点A，B，C，设若m，n的长度恰好相等，则有(　　)

A．A，B，C三点必在同一直线上

B．△ABC必为等腰三角形且∠B为顶角

C．△ABC必为直角三角形且∠B＝90°

D．△ABC必为等腰直角三角形

【答案】　C

【解析】选C　由|m|＝|n|，知A，B，C为一矩形的三顶点，且△ABC中∠B为直角．

10．设平面向量a1，a2，a3满足a1－a2＋a3＝0，如果平面向量b1，b2，b3满足|bi|＝2|ai|，且ai顺时针旋转30°后与bi同向，其中i＝1,2,3，则b1－b2＋b3＝________.

【答案】0

【解析】　将ai顺时针旋转30°后得ai′，则a1′－a2′＋a3′＝0.又∵bi与ai′同向，且|bi|＝2|ai|，

∴b1－b2＋b3＝0.

11．已知O为四边形ABCD所在平面外一点，且向量、满足等式.作图并观察四边形ABCD的形状，并证明．

【答案】见解析

【解析】通过作图(如图)可以发现四边形ABCD为平行四边形．

证明如下：

∵，

∴，∴，∴AB綊DC，

∴四边形ABCD为平行四边形．

素养达成

12．已知△ABC是等腰直角三角形，∠ACB＝90°，M是斜边AB的中点，＝a，＝b.

求证：(1)|a－b|＝|a|；

(2)|a＋(a－b)|＝|b|.

【答案】见解析

【解析】　因为△ABC是等腰直角三角形，∠ACB＝90°，

所以CA＝CB.

又M是斜边AB的中点，所以CM＝AM＝BM.

(1)因为－＝，又||＝||，

所以|a－b|＝|a|.

(2)因为M是斜边AB的中点，

所以＝，

所以a＋(a－b)＝＋(－)＝＋＝＋＝，

因为||＝||，

所以|a＋(a－b)|＝|b|.