【同步练习】高中数学人教A版(2019)必修第二册--6.2.2向量的减法运算 课时作业（含解析）

6．2.2　向量的减法运算

必备知识基础练　

1．在△ABC中，＝a，＝b，则＝(　　)

A．a＋b    B．－a＋(－b)

C．a－b    D．b－a

2.－＋＝(　　)

A．    B．

C．    D．

3．已知正六边形ABCDEF，则＋－＝(　　)

A．    B．

C．    D．

4．如图，已知平行四边形ABCD的对角线AC和BD相交于O，且＝a，＝b，则可以表示为(　　)

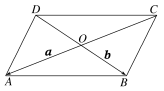
A.a＋b    B．a－bC．b－a    D．－a－b

5．化简：－＋＋＝(　　)

A．    B．0C．    D．

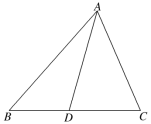
6．如图，在△ABC中，D是BC上一点，则＋－＝________．

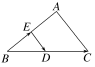
7．如图，在三角形ABC中，若D是边BC的中点，E是边AB上一点，则－＋＝________．

8.

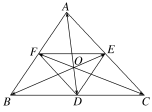
如图所示，已知＝a，＝b，＝c，＝d，＝e，＝f，试用a，b，c，d，e，f表示下列各式：

(1)－；

(2)＋；

(3)－.

关键能力综合练　

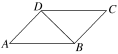
1.如图，在平行四边形ABCD中，下列结论正确的是(　　)

A．＝    B．＋＝

C．－＝    D．＋＝0

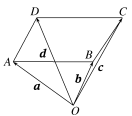
2.

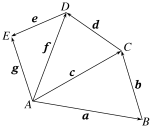
下列向量运算结果错误的是(　　)

A．a＋b＋d＝e

B．c＝f－d

C．a＝c－b

D．c＋d＋e＝g

3．下列各式的结果一定为零向量的是(　　)

A．＋－

B．＋－

C．－－＋

D．＋＋＋

4.

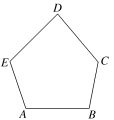
在五边形ABCDE中(如图)，下列运算结果为的是(　　)

A．＋－

B．＋＋

C．－

D．－

5．在四边形ABCD中，＝，若＝，则四边形ABCD是(　　)

A．菱形    B．矩形

C．正方形    D．不确定

6．(多选)对于菱形ABCD，给出下列各式，其中结论正确的为(　　)

A．＝

B．||＝||

C．|－|＝|＋|

D．|＋|＝|－|

7.

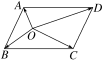
如图，已知O为平行四边形ABCD内一点，＝a，＝b，＝c，则＝________．

8．设平面内四边形ABCD及任一点O，＝a，＝b，＝c，＝d.若a＋c＝b＋d且|a－b|＝|a－d|，则四边形ABCD的形状是________．

9．化简：

(1)＋－－；

(2)(＋＋)－(－－).

10．若O是△ABC所在平面内一点，且满足|－|＝|－＋－|，试判断△ABC的形状．

核心素养升级练　

1．若||＝9，||＝4，则||的取值范围是(　　)

A．(5，13)    B．[4，5]

C．(5，9]    D．[5，13]

2．八卦是中国古老文化的深奥概念，其深邃的哲理解释了自然、社会现象．如图1所示的是八卦模型图，其平面图形记为图2中的正八边形ABCDEFGH，其中O为正八边形的中心，则－＝(　　)

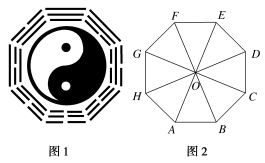
A.    B．C．    D．

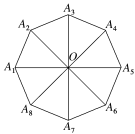
3．如图所示，中心为O的正八边形A1A2…A7A8中，ai＝ (i＝1，2，…，7)，bj＝ (j＝1，2，…，8)，则a2＋a5＋b2＋b5＋b7＝________．(结果用ai，bi表示)

6．2.2　向量的减法运算

必备知识基础练

1．答案：B

解析：因为＝a，＝b，所以＝－＝－－＝－a－b＝－a＋(－b)，故选B.

2．答案：B

解析：－＋＝＋＝，故选B.

3．答案：B

解析：由正六边形的特征可知：＝，＝，所以＋－＝＝，故选B.

4．答案：D

解析：在平行四边形ABCD中，依题意，＝－＝－a，而＝b，所以＝－＝－a－b.故选D.

5．答案：D

解析：－＋＋＝＋＋＝＋＝.故选D.

6．答案：

解析：由题意得＋－＝－＝.

7．答案：0

解析：因为D是边BC的中点，所以＝，所以－＋＝＋－＝－＝0.

8．解析：(1)－＝(－)－(－)＝d－a－b＋a＝d－b.

(2)＋＝(－)＋(－)＝b－a＋f－c.

(3)－＝(－)－(－)＝f－e－f＋c＝c－e.

关键能力综合练

1．答案：C

解析：对于A选项，＝，A错；对于B选项，＋＝，B错；对于C选项，－＝，C对；对于D选项，＋＝2，D错．故选C.

2．答案：A

解析：对于A，a＋b＋d＝＋＋＝＝f≠e，A错误；对于B，f－d＝－＝＋＝＝c，B正确；对于C，c－b＝－＝＋＝＝a，C正确；对于D，c＋d＋e＝＋＋＝＝g，D正确；故选A.

3．答案：B

解析：对于A，＋－＝2不一定为零向量，不选A；对于B，＋－＝－＋＝＋＝0，满足题意；对于C，－－＋＝＋－＝－＝2，不一定为零向量，不选C；对于D，＋＋＋＝＋＝，不一定为零向量，不选D.故选B.

4．答案：A

解析：A.＋－＝＋＝，正确；B.＋＋＝＋≠，不正确；C.－＝＋＝，不正确；D.－＝＋≠，不正确．故选A.

5．答案：B

解析：在四边形ABCD中，因为＝，所以四边形ABCD为平行四边形，又|－|＝|－|，即||＝||，所以平行四边形ABCD为矩形，故选B.

6．答案：BCD

解析：菱形中向量与的方向是不同的，但它们的模是相等的，所以B结论正确，A结论错误；因为|－|＝|＋|＝2||，|＋|＝2||，且||＝||，所以|－|＝|＋|，即C结论正确；因为|＋|＝|＋|＝||，|－|＝|＋|＝||，所以D结论正确．故选BCD.

7．答案：a＋c－b

解析：∵四边形ABCD为平行四边形，∴＝，∴＝＋＝＋＝＋－＝a＋c－b.

8．答案：菱形

解析：由a＋c＝b＋d得a－b＝d－c，即－＝－，∴＝，于是AB平行且等于CD，∴四边形ABCD为平行四边形，又|a－b|＝|a－d|，从而|－|＝|－|，∴||＝||，即四边形ABCD为菱形．

9．解析：(1)＋－－＝(－)＋(－)＝＋＝；

(2)(＋＋)－(－－)＝(＋)＋－＝＋＋＝＋＝0.

10．解析：∵－＋－＝＋，－＝，

∴|＋|＝||，

∴以AB、AC为邻边的平行四边形ABDC的两条对角线的长度相等，

∴此平行四边形为矩形，∴AB⊥AC.

∴△ABC是直角三角形．

核心素养升级练

1．答案：D

解析：||－||≤||＝|－|≤||＋||，所以5≤||≤13.故选D.

2．答案：B

解析：－＝－＝.

3．答案：b6